Hostname: page-component-7479d7b7d-fwgfc Total loading time: 0 Render date: 2024-07-11T08:51:43.404Z Has data issue: false hasContentIssue false
  • English
  • Français

TENSOR PRODUCTS OF STEINBERG ALGEBRAS

Part of: Rings and algebras arising under various constructions Topological and differentiable algebraic systems

Published online by Cambridge University Press:  04 September 2019

SIMON W. RIGBY Open the ORCID record for SIMON W. RIGBY [Opens in a new window]
SIMON W. RIGBY*
Affiliation:
Department of Mathematics: Algebra and Geometry, Ghent University, Belgium e-mail: simon.rigby@ugent.be
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that 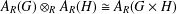$A_{R}(G)\otimes _{R}A_{R}(H)\cong A_{R}(G\times H)$ if 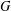$G$ and 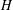$H$ are Hausdorff ample groupoids. As part of the proof, we give a new universal property of Steinberg algebras. We then consider the isomorphism problem for tensor products of Leavitt algebras, and show that no diagonal-preserving isomorphism exists between 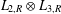$L_{2,R}\otimes L_{3,R}$ and 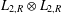$L_{2,R}\otimes L_{2,R}$. In fact, there are no unexpected diagonal-preserving isomorphisms between tensor products of finitely many Leavitt algebras. We give an easy proof that every $\ast$-isomorphism of Steinberg algebras over the integers preserves the diagonal, and it follows that 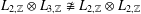$L_{2,\mathbb{Z}}\otimes L_{3,\mathbb{Z}}\not \cong L_{2,\mathbb{Z}}\otimes L_{2,\mathbb{Z}}$ (as $\ast$-rings).

Keywords

Steinberg algebrasample groupoidsLeavitt algebrasdiagonal-preserving isomorphisms

MSC classification

Primary: 16S99: None of the above, but in this section
Secondary: 16S10: Rings determined by universal properties (free algebras, coproducts, adjunction of inverses, etc.) 22A22: Topological groupoids (including differentiable and Lie groupoids)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 1 , August 2021 , pp. 111 - 126
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by L. O. Clark

References

Abrams, G., ‘Leavitt path algebras: the first decade’, Bull. Math. Sci. 5(1) (2015), 59–120.CrossRefGoogle Scholar
Abrams, G., Ara, P. and Siles Molina, M., Leavitt Path Algebras, Lecture Notes in Mathematics, 2191 (Springer, London, 2017).CrossRefGoogle Scholar
Abrams, G. and Aranda Pino, G., ‘The Leavitt path algebra of a graph’, J. Algebra 2(293) (2005), 319–334.CrossRefGoogle Scholar
Ara, P. and Cortiñas, G., ‘Tensor products of Leavitt path algebras’, Proc. Amer. Math. Soc. 141(8) (2013), 2629–2639.CrossRefGoogle Scholar
Ara, P., Moreno, M. A. and Pardo, E., ‘Nonstable K-theory for graph algebras’, Algebras Representation Theory 10(2) (2007), 157–178.CrossRefGoogle Scholar
Ara, P., Bosa, J., Hazrat, R. and Sims, A., ‘Reconstruction of graded groupoids from graded Steinberg algebras’, Forum Math. 29(5) (2017), 1023–1037.CrossRefGoogle Scholar
Ara, P., Hazrat, R., Li, H. and Sims, A., ‘Graded Steinberg algebras and their representations’, Algebra Number Theory 12(1) (2018).CrossRefGoogle Scholar
Austin, K. and Mitra, A., ‘Groupoid models of $C^{\ast }$ -algebras and Gelfand duality’, Preprint, 2018, arXiv:1804.00967v7.Google Scholar
Beuter, V. M. and Gonçalves, D., ‘The interplay between Steinberg algebras and skew rings’, J. Algebra 497 (2018), 337–362.CrossRefGoogle Scholar
Brown, J., Clark, L. O., Farthing, C. and Sims, A., ‘Simplicity of algebras associated to étale groupoids’, Semigroup Forum 88(2) (2014), 433–452.CrossRefGoogle Scholar
Brown, J. H., Clark, L. O. and an Huef, A., ‘Dense subalgebras of purely infinite simple groupoid $C^{\ast }$ -algebras’, Preprint, 2019, arXiv:1708.05130v2.Google Scholar
Brownlowe, N. and Sørensen, A. P. W., ‘L 2, ℤ ⊗ L 2, ℤ does not embed in L 2, ℤ’, J. Algebra 456 (2016), 1–22.CrossRefGoogle Scholar
Carlsen, T. M., ‘∗-isomorphism of Leavitt path algebras over ℤ’, Adv. Math. 324 (2018), 326–335.CrossRefGoogle Scholar
Carlsen, T. M. and Rout, J., ‘Diagonal-preserving graded isomorphisms of Steinberg algebras’, Commun. Contemp. Math. 20(06) (2018), 1750064.CrossRefGoogle Scholar
Clark, L. O. and Edie-Michell, C., ‘Uniqueness theorems for Steinberg algebras’, Algebras Representation Theory 18(4) (2015), 907–916.CrossRefGoogle Scholar
Clark, L. O. and Pangalela, Y. E. P., ‘Kumjian–Pask algebras of finitely aligned higher-rank graphs’, J. Algebra 482 (2017), 364–397.CrossRefGoogle Scholar
Clark, L. O. and Sims, A., ‘Equivalent groupoids have Morita equivalent Steinberg algebras’, J. Pure Appl. Algebra 219(6) (2015), 2062–2075.CrossRefGoogle Scholar
Clark, L. O., Farthing, C., Sims, A. and Tomforde, M., ‘A groupoid generalisation of Leavitt path algebras’, Semigroup Forum 89(3) (2014), 501–517.CrossRefGoogle Scholar
Clark, L. O., Martín Barquero, D., Martín González, C. and Siles Molina, M., ‘Using Steinberg algebras to study decomposability of Leavitt path algebras’, Forum Math. 29(6) (2016), 1311–1324.Google Scholar
Clark, L. O., Exel, R. and Pardo, E., ‘A generalized uniqueness theorem and the graded ideal structure of Steinberg algebras’, Forum Math. 30(3) (2018), 533–552.CrossRefGoogle Scholar
Clark, L. O., Edie-Michell, C., an Huef, A. and Sims, A., ‘Ideals of Steinberg algebras of strongly effective groupoids, with applications to Leavitt path algebras’, Trans. Amer. Math. Soc. 371(8) (2019), 5461–5486.CrossRefGoogle Scholar
Clark, L. O., Exel, R., Pardo, E., Sims, A. and Starling, C., ‘Simplicity of algebras associated to non-Hausdorff groupoids’, Trans. Amer. Math. Soc., to appear. Published online (10 June 2019).Google Scholar
Hazrat, R., Graded Rings and Graded Grothendieck Groups, London Mathematical Society Lecture Note Series, 435 (Cambridge University Press, Cambridge, 2016).CrossRefGoogle Scholar
Hazrat, R. and Li, H., Homology of étale groupoids, a graded approach, Preprint, 2018, arXiv:1806.03398v1.Google Scholar
Johansen, R. and Sørensen, A. P. W., ‘The Cuntz splice does not preserve ∗-isomorphism of Leavitt path algebras over ℤ’, J. Pure Appl. Algebra 220(12) (2016), 3966–3983.CrossRefGoogle Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J., ‘Graphs, groupoids, and Cuntz–Krieger algebras’, J. Funct. Anal. 144(2) (1997), 505–541.CrossRefGoogle Scholar
Leavitt, W. G., ‘The module type of a ring’, Trans. Amer. Math. Soc. 103(1) (1962), 113–130.CrossRefGoogle Scholar
Matui, H., ‘Étale groupoids arising from products of shifts of finite type’, Adv. Math. 303 (2016), 502–548.CrossRefGoogle Scholar
Paterson, A. L. T., Groupoids, Inverse Semigroups, and their Operator Algebras, Progress in Mathematics, 170 (Birkhäuser, Boston, 1999).CrossRefGoogle Scholar
Renault, J., A Groupoid Approach to C ∗ -Algebras, Lecture Notes in Mathematics, 793 (Springer, Berlin, 1980).CrossRefGoogle Scholar
Rigby, S. W., ‘The groupoid approach to Leavitt path algebras’, in: Leavitt Path Algebras and Classical K-Theory, (eds Ambily, A. A., Hazrat, R., and Sury, B.), Indian Statistical Institute Series (Springer, 2019), Ch. 2, 23–74.CrossRefGoogle Scholar
Steinberg, B., ‘A groupoid approach to discrete inverse semigroup algebras’, Preprint, 2009, arXiv:0903.3456v1.Google Scholar
Steinberg, B., ‘A groupoid approach to discrete inverse semigroup algebras’, Adv. Math. 223(2) (2010), 689–727.CrossRefGoogle Scholar
Steinberg, B., ‘Simplicity, primitivity and semiprimitivity of étale groupoid algebras with applications to inverse semigroup algebras’, J. Pure Appl. Algebra 220(3) (2016), 1035–1054.CrossRefGoogle Scholar
Steinberg, B., ‘Diagonal-preserving isomorphisms of étale groupoid algebras’, J. Algebra 518 (2019), 412–439.CrossRefGoogle Scholar
Steinberg, B., ‘Prime étale groupoid algebras with applications to inverse semigroup and Leavitt path algebras’, J. Pure Appl. Algebra 223 (2019), 2474–2488.CrossRefGoogle Scholar