Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-20T05:13:02.688Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME REMARKS ON THE 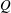$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Q$ CURVATURE TYPE PROBLEM ON 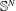$\mathbb{S}^N$

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  16 June 2014

SANJIBAN SANTRA
SANJIBAN SANTRA*
Affiliation:
School of Mathematics and Statistics, The University of Sydney, NSW 2006, Australia email sanjiban.santra@sydney.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove the existence, uniqueness and multiplicity of positive solutions of a nonlinear perturbed fourth-order problem related to the 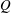$Q$ curvature.

Keywords

fourth-order problemcritical exponentuniquenessmultiplicity

MSC classification

Secondary: 35J10: Schrödinger operator 35J35: Variational methods for higher-order elliptic equations 35J65: Nonlinear boundary value problems for linear elliptic equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 1 , August 2014 , pp. 127 - 143
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Ambrosetti, A. and Badiale, M., ‘Variational perturbative methods and bifurcation of bound states from the essential spectrum’, Proc. Roy. Soc. Edinburgh Sect. A 128(6) (1998), 1131–1161.CrossRefGoogle Scholar
Ambrosetti, A., Garcia, A. and Peral, I., ‘Perturbation of Δ u + u N+2N−2 = 0, the scalar curvature problem in ℝN and related topics’, J. Funct. Anal. 165 (1999), 117–149.Google Scholar
Ambrosetti, A. and Malchiodi, A., Perturbation Methods and Semilinear Elliptic Problems on ℝN, Progress in Mathematics, 240 (Birkhäuser, Basel, 2006).Google Scholar
Ben Ayed, M. and El Mehdi, K., ‘The Paneitz curvature problem on lower-dimensional spheres’, Ann. Global Anal. Geom. 31(1) (2007), 1–36.Google Scholar
Branson, T., ‘Differential operators canonically associated to a conformal structure’, Math. Scand. 57 (1985), 293–345.CrossRefGoogle Scholar
Branson, T., Chang, A. and Yang, P., ‘Estimates and extremals for zeta function determinants on four-manifolds’, Comm. Math. Phys. 149(2) (1992), 241–262.CrossRefGoogle Scholar
Caristi, G. and Mitidieri, E., ‘Harnack inequality and applications to solutions of biharmonic equations’, in: Partial Differential Equations and Functional Analysis, Operator Theory Advances and Applications, 168 (Birkhäuser, Basel, 2006), 1–26.Google Scholar
Chang, A., ‘On Paneitz operator—a fourth-order partial differential equation in conformal geometry’, in: Harmonic Analysis and Partial Differential Equations; Essays in honor of Alberto P. Calderon, Chicago Lectures in Mathematics, 1999 (eds. Christ, M., Kenig, C. and Sadorsky, C.) (University of Chicago Press, 1996), Ch. 8, 127–150.Google Scholar
Chang, A., Gursky, M. and Yang, P., ‘The scalar curvature equation on 2- and 3-spheres’, Calc. Var. Partial Differential Equations 1 (1993), 205–229.Google Scholar
Chang, A. and Yang, P., ‘On a fourth order curvature invariant’, in: Spectral Problems in Geometry and Arithmetic, Contemporary Mathematics, 237 (American Mathematical Society, Providence, RI), 9–28.Google Scholar
Chtioui, H. and Rigane, A., ‘On the prescribed Q-curvature problem on SN’, J. Funct. Anal. 261(10) (2011), 2999–3043.Google Scholar
Djadli, Z., Hebey, E. and Ledoux, M., ‘Paneitz-type operators and applications’, Duke Math. J. 104(1) (2000), 129–169.Google Scholar
Djadli, Z., Malchiodi, A. and Ahmedou, M. O., ‘Prescribing a fourth order conformal invariant on the standard sphere, Part I: a perturbation result’, Commun. Contemp. Math. 4 (2002), 1–34.CrossRefGoogle Scholar
Esposito, P., ‘Perturbations of Paneitz–Branson operators on SN’, Rend. Semin. Mat. Univ. Padova 107 (2002), 165–184.Google Scholar
Esposito, P. and Robert, F., ‘Mountain pass critical points for Paneitz–Branson operators’, Calc. Var. Partial Differential Equations 15(4) (2002), 493–517.CrossRefGoogle Scholar
Felli, V., ‘Existence of conformal metrics on SN with prescribed fourth-order invariant’, Adv. Differential Equations 7(1) (2002), 47–76.Google Scholar
Gazzola, F., Grunau, H. C. and Sweers, G., ‘Polyharmonic boundary value problems’, in: Positivity Preserving and Nonlinear Higher Order Elliptic Equations in Bounded Domains, Lecture Notes in Mathematics, 1991 (Springer, Berlin, 2010).Google Scholar
Gursky, M., ‘The Weyl functional, de Rham cohomology, and Kahler–Einstein metrics’, Ann. of Math. (2) 148 (1998), 315–337.Google Scholar
Hebey, E. and Robert, F., ‘Asymptotic analysis for fourth order Paneitz equations with critical growth’, Adv. Calc. Var. 4(3) (2011), 229–275.Google Scholar
Kazdan, J. L. and Warner, F. W., ‘Curvature functions for compact 2-manifolds’, Ann. of Math. (2) 99(1) (1974), 14–47.Google Scholar
Lin, C. S., ‘A classification of solutions of a conformally invariant fourth order equation in ℝN’, Comment. Math. Helv. 73(2) (1998), 206–231.Google Scholar
Paneitz, S., ‘A quartic conformally covariant differential operator for arbitrary pseudo-Riemannian manifolds’, SIGMA Symmetry Integrability Geom. Methods Appl. 4 (2008), 1–3.Google Scholar
Prashanth, S., Santra, S. and Sarkar, A., ‘On the perturbed Q-curvature problem on S4’, J. Differential Equations 255(8) (2013), 2363–2391.CrossRefGoogle Scholar
Sandeep, K., ‘A compactness type result for Paneitz–Branson operators with critical nonlinearity’, Differential Integral Equations 18(5) (2005), 495–508.CrossRefGoogle Scholar
Wei, J. and Xu, X., ‘Classification of solutions of higher order conformally invariant equations’, Math. Ann. 313(2) (1999), 207–228.Google Scholar