Let 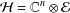${\mathcal{H}}=\mathbb{C}^{n}\otimes {\mathcal{E}}$ be the tensor product of a Euclidean space 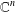$\mathbb{C}^{n}$ and a separable Hilbert space 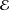${\mathcal{E}}$. Our main object is the operator 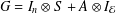$G=I_{n}\otimes S+A\otimes I_{{\mathcal{E}}}$, where 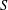$S$ is a normal operator in 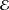${\mathcal{E}}$, 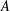$A$ is an 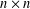$n\times n$ matrix, and 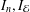$I_{n},I_{{\mathcal{E}}}$ are the unit operators in 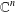$\mathbb{C}^{n}$ and 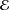${\mathcal{E}}$, respectively. Numerous differential operators with constant matrix coefficients are examples of operator 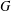$G$. In the present paper we show that 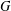$G$ is similar to an operator 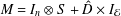$M=I_{n}\otimes S+\hat{D}\times I_{{\mathcal{E}}}$ where $\hat{D}$ is a block matrix, each block of which has a unique eigenvalue. We also obtain a bound for the condition number. That bound enables us to establish norm estimates for functions of $G$, nonregular on the closed convex hull 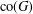$\operatorname{co}(G)$ of the spectrum of 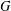$G$. The functions 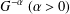$G^{-\unicode[STIX]{x1D6FC}}\;(\unicode[STIX]{x1D6FC}>0)$ and 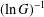$(\ln G)^{-1}$ are examples of such functions. In addition, in the appropriate situations we improve the previously published estimates for the resolvent and functions of 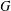$G$ regular on 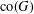$\operatorname{co}(G)$. Since differential operators with variable coefficients often can be considered as perturbations of operators with constant coefficients, the results mentioned above give us estimates for functions and bounds for the spectra of differential operators with variable coefficients.