Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-19T22:41:42.286Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SUB-CLASS SIZES OF FINITE GROUPS

Part of: Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  08 April 2019

GUOHUA QIAN  and
YONG YANG
GUOHUA QIAN*
Affiliation:
Department of Mathematics, Changshu Institute of Technology, Changshu, Jiangsu215500, China email ghqian2000@163.com
YONG YANG*
Affiliation:
Key Laboratory of Group and Graph Theories and Applications, Chongqing University of Arts and Sciences, Chongqing402160, China Department of Mathematics, Texas State University, San Marcos, TX78666, USA email yang@txstate.edu
*
✉ email yang@txstate.edu
✉ email yang@txstate.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

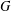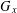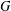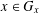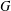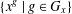For every element $x$ of a finite group $G$, there always exists a unique minimal subnormal subgroup, say, $G_{x}$ of $G$ such that $x\in G_{x}$. The sub-class of $G$ in which $x$ lies is defined by $\{x^{g}\mid g\in G_{x}\}$. The aim of this paper is to investigate the influence of the sub-class sizes on the structure of finite groups.

Keywords

finite groupclass size

MSC classification

Primary: 20E45: Conjugacy classes
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 3 , June 2020 , pp. 402 - 411
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Email addresses for correspondence: email ghqian2000@163.com, yang@txstate.edu.

This project was supported by the NSF of China (nos. 11471054, 11671063, and 11871011), the NSF of Jiangsu Province (no. BK20161265), the Natural Science Foundation of Chongqing (cstc2016jcyjA0065, cstc2018jcyjAX0060), and a grant from the Simons Foundation (no. 499532).

References

Camina, A. R., ‘Arithmetical conditions on the conjugacy class numbers of a finite group’, J. Lond. Math. Soc. 5 (1972), 127–132.Google Scholar
Camina, A. R. and Camina, R. D., ‘The influence of conjugacy class sizes on the structure of finite groups: a survey’, Asian-Eur. J. Math. 4 (2011), 559–588.Google Scholar
Casolo, C. and Dolfi, S., ‘Conjugacy class lengths of metanilpotent groups’, Rend. Semin. Mat. Univ. Padova 96 (1996), 121–130.Google Scholar
Casolo, C. and Dolfi, S., ‘Prime divisors of irreducible character degrees and of conjugacy class sizes in finite groups’, J. Group Theory 10 (2007), 571–583.Google Scholar
Chillag, D. and Herzog, M., ‘On the length of the congugacy classes of finite groups’, J. Algebra 131 (1990), 110–125.Google Scholar
Isaacs, I. M., Finite Group Theory, Graduate Studies in Mathematics, 92 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Itô, N., ‘On finite groups with given conjugate types. I’, Nagoya Math. J. 6 (1953), 17–28.Google Scholar
Huppert, B., Character Theory of Finite Groups (Walter de Gruyter, Berlin, 1998).Google Scholar
Kurzweil, H. and Stellmacher, B., The Theory of Finite Groups (Springer, New York, 2004).Google Scholar
Liu, X., Wang, Y. and Wei, H., ‘Notes on the length of conjugacy classes of finite groups’, J. Pure Appl. Algebra 196 (2005), 111–117.Google Scholar
Zhang, J., ‘On the lengths of conjugacy classes’, Comm. Algebra 26 (1998), 2395–2400.Google Scholar