No CrossRef data available.
Article contents
ON GENERALIZED THUE–MORSE FUNCTIONS AND THEIR VALUES
Part of:
Algebraic number theory: global fields
Diophantine approximation, transcendental number theory
Published online by Cambridge University Press: 11 March 2019
Abstract
In this paper we extend and generalize, up to a natural bound of the method, our previous work Badziahin and Zorin [‘Thue–Morse constant is not badly approximable’, Int. Math. Res. Not. IMRN 19 (2015), 9618–9637] where we proved, among other things, that the Thue–Morse constant is not badly approximable. Here we consider Laurent series defined with infinite products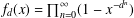 
$f_{d}(x)=\prod _{n=0}^{\infty }(1-x^{-d^{n}})$, 
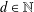$d\in \mathbb{N}$, 
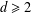$d\geq 2$, which generalize the generating function 
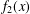$f_{2}(x)$ of the Thue–Morse number, and study their continued fraction expansion. In particular, we show that the convergents of 
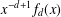$x^{-d+1}f_{d}(x)$ have a regular structure. We also address the question of whether the corresponding Mahler numbers 
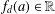$f_{d}(a)\in \mathbb{R}$, 
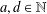$a,d\in \mathbb{N}$, 
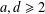$a,d\geq 2$, are badly approximable.
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
Dzmitry Badziahin acknowledges the support of EPSRC Grant EP/E061613/1. Evgeniy Zorin acknowledges the support of EPSRC Grant EP/M021858/1.
References
Allouche, J. P., Mendès France, M. and van der Poorten, A. J., ‘An infinite product with bounded partial quotients’, Acta Arith. 59 (1991), 171–182.Google Scholar
Badziahin, D. A. and Zorin, E., ‘Thue–Morse constant is not badly approximable’, Int. Math. Res. Not. IMRN 19 (2015), 9618–9637.Google Scholar
Bugeaud, Y., ‘On the irrationality exponent of the Thue–Morse–Mahler numbers’, Ann. Inst. Fourier (Grenoble) 61(5) (2011), 2065–2076.Google Scholar
Bugeaud, Y., Han, G.-N., Wen, Z.-Y. and Yao, J.-Y., ‘Hankel determinants, Padé approximations, and irrationality exponents’, Int. Math. Res. Not. IMRN 5 (2016), 1467–1496.Google Scholar
Mendès France, M. and van der Poorten, A. J., ‘From geometry to Euler identities’, Theoret. Comput. Sci. 65(2) (1989), 213–220.Google Scholar
Mendès France, M. and van der Poorten, A. J., ‘Some explicit continued fraction expansions’, Mathematika 38(1) (1991), 1–9.Google Scholar
Montgomery, P. L., ‘New solutions of a p-1 ≡ 1 mod p 2’, Math. Comp. 61 (1993), 361–363.Google Scholar
van der Poorten, A. J., ‘Formal power series and their continued fraction expansion’, in: Algorithmic Number Theory (Proc. Third International Symposium, ANTS-III, Portland, Oregon, June 1998), Springer Lecture Notes in Computer Science, 1423 (1998), 358–371.Google Scholar
Ribenboim, P., Die Welt der Primzahlen: Geheimnisse und Rekorde (Springer, New York, 2004), 237 (in German).Google Scholar