Article contents
ON A FUNCTION MODULE WITH APPROXIMATE HYPERPLANE SERIES PROPERTY
Published online by Cambridge University Press: 03 July 2019
Abstract
We present a sufficient and necessary condition for a function module space 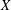 $X$ to have the approximate hyperplane series property (AHSP). As a consequence, we have that the space
$X$ to have the approximate hyperplane series property (AHSP). As a consequence, we have that the space 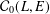 ${\mathcal{C}}_{0}(L,E)$ of bounded and continuous
${\mathcal{C}}_{0}(L,E)$ of bounded and continuous 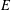 $E$-valued mappings defined on the locally compact Hausdorff space
$E$-valued mappings defined on the locally compact Hausdorff space 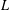 $L$ has AHSP if and only if
$L$ has AHSP if and only if 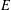 $E$ has AHSP.
$E$ has AHSP.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by




