Article contents
HARDY SPACES ON METRIC MEASURE SPACES WITH GENERALIZED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
Published online by Cambridge University Press: 14 August 2017
Abstract
Hardy space theory has been studied on manifolds or metric measure spaces equipped with either Gaussian or sub-Gaussian heat kernel behaviour. However, there are natural examples where one finds a mix of both behaviours (locally Gaussian and at infinity sub-Gaussian), in which case the previous theory does not apply. Still we define molecular and square function Hardy spaces using appropriate scaling, and we show that they agree with Lebesgue spaces in some range. Besides, counterexamples are given in this setting that the
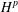 $H^{p}$
space corresponding to Gaussian estimates may not coincide with
$H^{p}$
space corresponding to Gaussian estimates may not coincide with
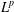 $L^{p}$
. As a motivation for this theory, we show that the Riesz transform maps our Hardy space
$L^{p}$
. As a motivation for this theory, we show that the Riesz transform maps our Hardy space
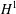 $H^{1}$
into
$H^{1}$
into
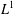 $L^{1}$
.
$L^{1}$
.
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by




