Article contents
GENERALIZED JORDAN DERIVATIONS ON SEMIPRIME RINGS
Published online by Cambridge University Press: 29 July 2019
Abstract
The purpose of this note is to prove the following. Suppose 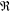 $\mathfrak{R}$ is a semiprime unity ring having an idempotent element
$\mathfrak{R}$ is a semiprime unity ring having an idempotent element  $e$ (
$e$ (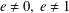 $e\neq 0,~e\neq 1$) which satisfies mild conditions. It is shown that every additive generalized Jordan derivation on
$e\neq 0,~e\neq 1$) which satisfies mild conditions. It is shown that every additive generalized Jordan derivation on 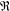 $\mathfrak{R}$ is a generalized derivation.
$\mathfrak{R}$ is a generalized derivation.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by





