Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-26T05:55:34.676Z Has data issue: false hasContentIssue false
  • English
  • Français

FREE CENTRE-BY-NILPOTENT-BY-ABELIAN LIE RINGS OF RANK 2

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  07 May 2015

MARIA ALEXANDROU  and
RALPH STÖHR
MARIA ALEXANDROU
Affiliation:
School of Mathematics, University of Manchester, Alan Turing Building, Manchester M13 9PL, UK email maria.alexandrou@postgrad.manchester.ac.uk
RALPH STÖHR*
Affiliation:
School of Mathematics, University of Manchester, Alan Turing Building, Manchester M13 9PL, UK email ralph.stohr@manchester.ac.uk
*
✉ralph.stohr@manchester.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the free Lie ring of rank 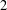$2$ in the variety of all centre-by-nilpotent-by-abelian Lie rings of derived length 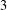$3$. This is the quotient 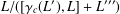$L/([\unicode[STIX]{x1D6FE}_{c}(L^{\prime }),L]+L^{\prime \prime \prime })$ with 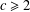$c\geqslant 2$ where 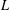$L$ is the free Lie ring of rank 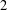$2$, 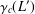$\unicode[STIX]{x1D6FE}_{c}(L^{\prime })$ is the $c$th term of the lower central series of the derived ideal 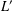$L^{\prime }$ of 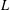$L$, and 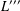$L^{\prime \prime \prime }$ is the third term of the derived series of 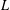$L$. We show that the quotient 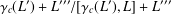$\unicode[STIX]{x1D6FE}_{c}(L^{\prime })+L^{\prime \prime \prime }/[\unicode[STIX]{x1D6FE}_{c}(L^{\prime }),L]+L^{\prime \prime \prime }$ is a direct sum of a free abelian group and a torsion group of exponent $c$. We exhibit an explicit generating set for the torsion subgroup.

Keywords

free Lie rings

MSC classification

Primary: 17B01: Identities, free Lie (super)algebras
Secondary: 17B55: Homological methods in Lie (super)algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 1 , February 2017 , pp. 63 - 73
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Bakhturin, Y. A., Identical relations in Lie algebras (Nauka, Moscow, 1985), (in Russian). English translation: VNU Science Press, Utrecht, 1987.Google Scholar
Drensky, V., ‘Torsion in the additive group of relatively free Lie rings’, Bull. Aust. Math. Soc. 33(1) (1986), 81–87.Google Scholar
Gupta, C. K., ‘The free centre-by-metabelian groups’, J. Aust. Math. Soc. 16 (1973), 294–299.Google Scholar
Hannebauer, T. and Stöhr, R., ‘Homology of groups with coefficients in free metabelian Lie powers and exterior powers of relation modules and applications to group theory’, Rend. Circ. Mat. Palermo (2) Suppl. 23 (1990), 77–113; Proc. Second Internat. Group Theory Conf., Bressanone, 1989.Google Scholar
Johnson, M. and Stöhr, R., ‘Free central extensions of groups and modular Lie powers of relation modules’, Proc. Amer. Math. Soc. 138(11) (2010), 3807–3814.CrossRefGoogle Scholar
Kovács, L. G. and Stöhr, R., ‘Free centre-by-metabelian Lie algebras in characteristic 2’, Bull. Lond. Math. Soc. 46 (2014), 491–502.Google Scholar
Kuz’min, Yu. V., ‘Free center-by-metabelian groups, Lie algebras and D-groups’, Izv. Akad. Nauk SSSR Ser. Mat. 41(1) (1977), 3–33; 231 (in Russian). English translation: Math. USSR Izv. 11 (1977), no. 1, 1–30.Google Scholar
Mac Lane, S., Homology, Grundlehren der mathematischen Wissenschaften, 114 (Springer, Berlin, 1963).Google Scholar
Mansuroǧlu, N. and Stöhr, R., ‘Free centre-by-metabelian Lie rings’, Q. J. Math. 65(2) (2014), 555–579.Google Scholar
Stöhr, R., ‘Homology of metabelian Lie powers and torsion in relatively free groups’, Q. J. Math. 43(3) (1992), 361–380.Google Scholar
Stöhr, R., ‘Symmetric powers, metabelian Lie powers and torsion in groups’, Math. Proc. Cambridge Philos. Soc. 118(3) (1995), 449–466.Google Scholar
Ridley, J. N., ‘The free centre-by-metabelian group of rank two’, Proc. Lond. Math. Soc. (3) 20 (1970), 321–347.Google Scholar
Zerck, R., ‘On free centre-by-nilpotent-by-abelian groups and Lie rings’, Preprint, 1991. Akad. Wiss. DDR, Inst. Math. P-MATH-15/91, 29 p.Google Scholar