Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-16T18:35:05.173Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FINITE FOURIER TRANSFORM OF CLASSICAL POLYNOMIALS

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  04 December 2014

ATUL DIXIT ,
LIN JIU ,
VICTOR H. MOLL  and
CHRISTOPHE VIGNAT
ATUL DIXIT
Affiliation:
Department of Mathematics, Tulane University, New Orleans, LA 70118, USA email adixit@tulane.edu
LIN JIU
Affiliation:
Department of Mathematics, Tulane University, New Orleans, LA 70118, USA email ljiu@tulane.edu
VICTOR H. MOLL*
Affiliation:
Department of Mathematics, Tulane University, New Orleans, LA 70118, USA email vhm@tulane.edu
CHRISTOPHE VIGNAT
Affiliation:
Department of Mathematics, Tulane University, New Orleans, LA 70118, USA email cvignat@math.tulane.edu LSS-Supelec, Universit’e Orsay Paris Sud 11, France
*
✉vhm@tulane.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The finite Fourier transform of a family of orthogonal polynomials is the usual transform of these polynomials extended by 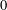$0$ outside their natural domain of orthogonality. Explicit expressions are given for the Legendre, Jacobi, Gegenbauer and Chebyshev families.

Keywords

Fourier transformorthogonal polynomialsJacobi polynomials

MSC classification

Primary: 33C45: Orthogonal polynomials and functions of hypergeometric type (Jacobi, Laguerre, Hermite, Askey scheme, etc.)
Secondary: 33C47: Other special orthogonal polynomials and functions 33C10: Bessel and Airy functions, cylinder functions, $_0F_1$ 42C10: Fourier series in special orthogonal functions (Legendre polynomials, Walsh functions, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 2 , April 2015 , pp. 145 - 160
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Coffey, M., Dixit, A., Moll, V., Straub, A. and Vignat, C., ‘The Zagier modification of Bernoulli polynomials. Part II: arithmetic properties of denominators’, Ramanujan J. 35 (2014), 361–390.Google Scholar
Dixit, A., Glasser, L., Mahlburg, K., Moll, V. and Vignat, C., The Zagier polynomials. Part III. Fourier type expansions, in preparation (2014).Google Scholar
Dixit, A., Moll, V. and Vignat, C., ‘The Zagier modification of Bernoulli numbers and a polynomial extension. Part I’, Ramanujan J. 33 (2014), 379–422.CrossRefGoogle Scholar
Erdélyi, A., Tables of Integral Transforms, 1st edn, Vol. I (McGraw-Hill, New York, 1954).Google Scholar
Fokas, A. S., Iserles, A. and Smitherman, S. A., ‘The unified method in polygonal domains via the explicit Fourier transform of Legendre polynomials’, in: Unified Transforms (eds. Fokas, A. S. and Pelloni, B.) (SIAM, Philadelphia, PA, 2014).Google Scholar
Gradshteyn, I. S., Ryzhik, I. M. and Zwillinger, D., Table of Integrals, Series, and Products, 7th edn (ed. Jeffrey, A.) (Academic Press, New York, 2007).Google Scholar
Greene, N., ‘Formulas for the Fourier series of orthogonal polynomials in terms of special functions’, Int. J. Math. Models Methods Appl. Sci. 2 (2008), 317–320.Google Scholar
Hale, N. and Townsend, A., An algorithm for the convolution of Legendre series, Preprint, 2014.CrossRefGoogle Scholar
Hardy, G. H. and Rogosinski, W. W., Fourier Series, 2nd edn (Cambridge University Press, Cambridge, 1950).Google Scholar
Neuschel, T., ‘Asymptotics for Ménage polynomials and certain hypergeometric polynomials of type 3F 1’, J. Approx. Theory 164 (2012), 981–1006.Google Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clark, C. W. (eds) NIST Handbook of Mathematical Functions (Cambridge University Press, Cambridge, 2010).Google Scholar
Prudnikov, A. P., Brychkov, Yu. A. and Marichev, O. I., Integrals and Series, Special Functions, 2 (Gordon and Breach, 1986).Google Scholar
Prudnikov, A. P., Brychkov, Yu. A. and Marichev, O. I., Integrals and Series, More Special Functions, 3 (Gordon and Breach, 1998).Google Scholar
Temme, N. M., Special Functions. An Introduction to the Classical Functions of Mathematical Physics (John Wiley, New York, 1996).CrossRefGoogle Scholar
Touchard, J., ‘Sur un problème de permutations’, C. R. Acad. Sci. Paris 198 (1934), 631–633.Google Scholar