Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-25T07:31:20.966Z Has data issue: false hasContentIssue false
  • English
  • Français

DILATIONS OF INTERACTION GROUPS THAT EXTEND ACTIONS OF ORE SEMIGROUPS

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  30 January 2018

FERNANDO ABADIE
FERNANDO ABADIE*
Affiliation:
Centro de Matemática-FC, Universidad de la República. 11 400, Iguá 4225, Montevideo, Uruguay email fabadie@cmat.edu.uy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if a unital injective endomorphism of a 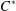$C^{\ast }$-algebra admits a transfer operator, then both of them are compressions of mutually inverse automorphisms of a bigger algebra. More generally, every interaction group – in the sense of Exel – extending an action of an Ore semigroup by injective unital endomorphisms of a 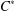$C^{\ast }$-algebra, admits a dilation to an action of the corresponding enveloping group on another unital 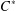$C^{\ast }$-algebra, of which the former is a 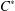$C^{\ast }$-subalgebra: the interaction group is obtained by composing the action with a conditional expectation. The dilation is essentially unique if a certain natural condition of minimality is imposed, and it is faithful if and only if the interaction group is also faithful.

Keywords

transfer operatorconditional expectationinteraction group

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 104 , Issue 2 , April 2018 , pp. 145 - 161
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Abadie, F., ‘Enveloping actions and Takai duality for partial actions’, J. Funct. Anal. 197 (2003), 14–67.CrossRefGoogle Scholar
Abadie, F., ‘On partial actions and groupoids’, Proc. Amer. Math. Soc. 132(4) (2004), 1037–1047.CrossRefGoogle Scholar
Brownlowe, N. and Raeburn, I., ‘Exel’s crossed products and relative Cuntz–Pimsner algebras’, Math. Proc. Cambridge Philos. Soc. 141(3) (2006), 497–508.CrossRefGoogle Scholar
de Castro, G. G., ‘C*-algebras associated with iterated function systems’, in: Operator Structures and Dynamical Systems, Contemp. Math., 503 (American Mathematical Society, Providence, RI, 2009), 27–37.CrossRefGoogle Scholar
Deaconu, V., ‘C*-algebras of commuting endomorphisms’, in: Advances in Operator Algebras and Mathematical Physics, Theta Ser. Adv. Math., 5 (Theta, Bucharest, 2005), 47–55.Google Scholar
Exel, R., ‘A new look at the crossed-product of a C*-algebra by an endomorphism’, Ergod. Th. & Dynam. Sys. 23(6) (2003), 1733–1750.CrossRefGoogle Scholar
Exel, R., ‘Crossed-products by finite index endomorphisms and KMS states’, J. Funct. Anal. 199(1) (2003), 153–188.CrossRefGoogle Scholar
Exel, R., ‘Interactions’, J. Funct. Anal. 244(1) (2007), 26–67.CrossRefGoogle Scholar
Exel, R., ‘A new look at the crossed-product of a C*-algebra by a semigroup of endomorphisms’, Ergod. Th. & Dynam. Sys. 28(3) (2008), 749–789.CrossRefGoogle Scholar
Exel, R. and Renault, J., ‘Semigroups of local homeomorphisms and interaction groups’, Ergod. Th. & Dynam. Sys. 27(6) (2007), 1737–1771.CrossRefGoogle Scholar
Exel, R. and Vershik, A., ‘C*-algebras of irreversible dynamical systems’, Canad. J. Math. 58(1) (2006), 39–63.CrossRefGoogle Scholar
Laca, M., ‘From endomorphisms to automorphisms and back: dilations and full corners’, J. Lond. Math. Soc. (2) 61(3) (2000), 893–904.CrossRefGoogle Scholar
Larsen, N. S., ‘Crossed products by abelian semigroups via transfer operators’, Ergod. Th. & Dynam. Sys. 30(4) (2010), 1147–1164.CrossRefGoogle Scholar
Royer, D., ‘The crossed product by a partial endomorphism and the covariance algebra’, J. Math. Anal. Appl. 323 (2006), 33–41.CrossRefGoogle Scholar