Hostname: page-component-5c6d5d7d68-wbk2r Total loading time: 0 Render date: 2024-08-18T14:43:55.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering Theorems for FINASIGS VIII—almost all conjugacy classes in An have exponent ≤4

Part of: Representation theory of groups

Published online by Cambridge University Press:  09 April 2009

J. L. Brenner
J. L. Brenner
Affiliation:
10 Phillips Road Palo Alto, CA 94303
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

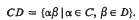The product of two subsets C, D of a group is defined as . The power Ce is defined inductively by C0 = {1}, Ce = CCe−1 = Ce−1C. It is known that in the alternating group An, n > 4, there is a conjugacy class C such that CC covers An. On the other hand, there is a conjugacy class D such that not only DD≠An, but even De≠An for e<[n/2]. It may be conjectured that as n ← ∞, almost all classes C satisfy C3 = An. In this article, it is shown that as n ← ∞, almost all classes C satisfy C4 = An.

MSC classification

Secondary: 20D05: Finite simple groups and their classification
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 25 , Issue 2 , March 1978 , pp. 210 - 214
Copyright
Copyright © Australian Mathematical Society 1978

References

REFERENCES

Brenner, J. L. (1973), “Covering theorems for nonabelian simple groups II”, J. Combinatorial Theory (A) 14, 264–269.CrossRefGoogle Scholar
Brenner, J. L. (1975), “Covering theorems for finite nonabelian simple groups, IV”, Jñānabha, Section A, 3, 77–84.Google Scholar
Brenner, J. L. (1977), “Covering theorems for FINASIGS. IX”, Ars Combinatoria 4, 151–176.Google Scholar
Brenner, J. L. and Carlitz, L. (1976), “Covering theorems for finite nonabelian simple groups. III. Solution of the equation x2 + y2 + y−2 = a in a finite field”, Rend. Seminario Mat. di Padova 55, 81–90.Google Scholar
Brenner, J. L., Cranwell, R. M. and Riddell, J. (1974), “Covering theorems for nonabelian simple groups. V”, Pacific J. Math. 58, 55–60.CrossRefGoogle Scholar
Brenner, J. L., Randall, M. and Riddell, J. (1974), “Covering theorems for nonabelian simple groups. I”, Colloq. Math. 32, 39–48.CrossRefGoogle Scholar
Brenner, J. L. and Riddell, J. (1976), “Covering theorems for nonabelian simple groups. VII. Asymptotics in the alternating groups”, Ars Combinatoria 1, 77–108.Google Scholar
Brenner, J. L. and Riddell, J. (1977), “Noncanonical factorization of a permutation ( ≡ Covering Theorems VI)” American Mathematical Monthly, 84, no. 1, 39–40.Google Scholar
Hardy, G. H. and Ramanujan, S. (1918), “Asymptotic formulae in combinatory analysis”, Proc. London Math. Soc. (2) 17, 75–115.Google Scholar
Herzog, M. and Reid, K. B. (1976), “Number of factors in k-cycle decompositions of permutations”, Proc. 4th Australian Conference Combinatorial Math (Springer Lecture Notes in Math 560, 123–131).Google Scholar
Herzog, M. and Reid, K. B. (1977), “Representation of permutations as products of cycles of fixed length”, J. Austral. Math. Soc. 22, (Ser. A), 321–331.Google Scholar
Rabinovič, E. B. and Feiĩberg, V. Z. (1974), “Normal divisors of a 2-transitive group of automorphisms of a linearly ordered set”, Mat. Sbornik 93 (135), no. 2, 189–202.Google Scholar
Scott, W. R. (1964), Group Theory (Prentice-Hall, Englewood Cliffs, N.J.).Google Scholar