Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-19T16:45:01.391Z Has data issue: false hasContentIssue false
  • English
  • Français

Complex inversion theorems for generalized Stieltjes transforms

Published online by Cambridge University Press:  09 April 2009

Angelina Byrne  and
E. R. Love
Angelina Byrne
Affiliation:
Department of Mathematics, State College of Victoria at Melbourne, Australia
E. R. Love
Affiliation:
Department of Mathematics, University of Melbourne, Porkville, 3052, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we seek to establish some “complex inversion formulae” for the generalized Stieltjes transform 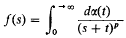for all s in the cut plane, supposing that p is any complex number except zero and the negative integers. The “cut plane” means all complex numbers except those which are negative real or zero.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 18 , Issue 3 , November 1974 , pp. 328 - 358
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Widder, D. V., The Laplace Transform (Princeton 1946).Google Scholar
[2]Sumner, D. B., ‘An inversion formula for the Generalized Stieltjes Transform’, Bull. American Math. Soc. 55 (1949), 174–183.CrossRefGoogle Scholar
[3]Hirschman, I. I. and Widder, D. V., The Convolution Transform (Princeton 1955).Google Scholar
[4]Pandey, J. N. and Zemanian, A. H., ‘Complex inversion for the Generalized Convolution Transformation’, Pacific Journ. of Math. 25 (1968), 147–157.CrossRefGoogle Scholar
[5]Erdélyi, A. and others, Tables of Integral Transforms, vol. 2, Bateman Manuscript Project (McGraw-Hill 1954).Google Scholar
[6]Titchmarsh, E. C., Theory of Fourier Integrals (Oxford 1937).Google Scholar
[7]Wiener, N., ‘The Quadratic Variation of a function and its Fourier coefficients’, J. Massachusetts Inst. of Tech. 3 (1924), 73–94.Google Scholar
[8]Young, L. C., ‘An inequality of the Hölder type, connected with Stieltjes integration’, Acta Math. 67 (1936), 251–282.CrossRefGoogle Scholar
[9]Love, E. R. and Young, L. C., ‘Sur une classe de fonctionnelles linéaires’, Fund. Math. 28 (1937), 243–257.CrossRefGoogle Scholar
[10]Love, E. R. and Young, L. C., ‘On fractional integration by parts’, Proc. London Math. Soc. (2) 44 (1938), 1–35.CrossRefGoogle Scholar
[11]Musielak, J. and Orlicz, W., ‘On generalized variations (I)’, Studia Math. 18 (1959), 11–41.CrossRefGoogle Scholar
[12]Love, E. R., ‘Fractional derivatives of imaginary order’, J. London Math. Soc. (2) 3 (1971), 241–259.CrossRefGoogle Scholar