Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Masser, D. W.
1982.
A vanishing theorem for power series.
Inventiones Mathematicae,
Vol. 67,
Issue. 2,
p.
275.
Nishioka, K.
1989.
Evertse theorem in algebraic independence.
Archiv der Mathematik,
Vol. 53,
Issue. 2,
p.
159.
Shallit, Jeffrey
1999.
Emerging Applications of Number Theory.
Vol. 109,
Issue. ,
p.
547.
Hančl, Jaroslav
2004.
A Criterion for Linear Independence of Series.
Rocky Mountain Journal of Mathematics,
Vol. 34,
Issue. 1,
Tanaka, Taka-aki
2004.
Algebraic independence of the values of Mahler functions associated with a certain continued fraction expansion.
Journal of Number Theory,
Vol. 105,
Issue. 1,
p.
38.
Tanaka, Taka-aki
2009.
Conditions for the algebraic independence of certain series involving continued fractions and generated by linear recurrences.
Journal of Number Theory,
Vol. 129,
Issue. 12,
p.
3081.
Bundschuh, Peter
and
Väänänen, Keijo
2016.
From Arithmetic to Zeta-Functions.
p.
91.
Tanaka, Taka-aki
and
Tanuma, Yusuke
2018.
Algebraic independence of the values of the Hecke–Mahler series and its derivatives at algebraic numbers.
International Journal of Number Theory,
Vol. 14,
Issue. 09,
p.
2369.
Tanuma, Yusuke
2020.
Algebraic independence of the values of certain series and their derivatives involving the Hecke-Mahler series.
Journal of Number Theory,
Vol. 210,
Issue. ,
p.
231.
Roques, Julien
2021.
On the Local Structure of Mahler Systems.
International Mathematics Research Notices,
Vol. 2021,
Issue. 13,
p.
9937.
IDE, Haruki
TANAKA, Taka-aki
and
TOYAMA, Kento
2022.
Algebraic Independence of the Values of Power Series and Their Derivatives Generated by Linear Recurrences.
Tokyo Journal of Mathematics,
Vol. 45,
Issue. 2,
ROQUES, Julien
2024.
Frobenius method for Mahler equations.
Journal of the Mathematical Society of Japan,
Vol. 76,
Issue. 1,
Faverjon, C.
and
Roques, J.
2024.
Hahn series and Mahler equations: Algorithmic aspects.
Journal of the London Mathematical Society,
Vol. 110,
Issue. 1,
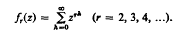 We show that the functions fr(z) are algebraically independent over the rational functions Further, if αrs (r = 2, 3, 4, hellip; s = 1, 2, 3, hellip) are algebraic numbers with 0 < |αrs|, we obtain an explicit necessary and sufficient condition for the algebraic independence of the numbers fr(αrs) over the rationals.
We show that the functions fr(z) are algebraically independent over the rational functions Further, if αrs (r = 2, 3, 4, hellip; s = 1, 2, 3, hellip) are algebraic numbers with 0 < |αrs|, we obtain an explicit necessary and sufficient condition for the algebraic independence of the numbers fr(αrs) over the rationals.



