Article contents
Two step iteration of almost disjoint families
Published online by Cambridge University Press: 12 March 2014
Extract
Let E be an infinite set, and [E]ω the set of all countably infinite subsets of E. A family 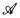 ⊂ [E]ω is said to be almost disjoint (respectively, pairwise disjoint) provided for A, B ∈
⊂ [E]ω is said to be almost disjoint (respectively, pairwise disjoint) provided for A, B ∈ 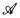 , if A ≠ B then A ∩ B is finite (respectively, A ∩ B is empty). Moreover, an infinite family A is said to be a maximal almost disjoint family provided it is an infinite almost disjoint family not properly contained in any almost disjoint family. In this paper we are concerned with the following set of topological spaces defined from (maximal) almost disjoint families of infinite subsets of the natural numbers ω.
, if A ≠ B then A ∩ B is finite (respectively, A ∩ B is empty). Moreover, an infinite family A is said to be a maximal almost disjoint family provided it is an infinite almost disjoint family not properly contained in any almost disjoint family. In this paper we are concerned with the following set of topological spaces defined from (maximal) almost disjoint families of infinite subsets of the natural numbers ω.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 1
- Cited by




