Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-27T01:24:12.978Z Has data issue: false hasContentIssue false
  • English
  • Français

TOWERS IN FILTERS, CARDINAL INVARIANTS, AND LUZIN TYPE FAMILIES

Published online by Cambridge University Press:  23 October 2018

JÖRG BRENDLE ,
BARNABÁS FARKAS  and
JONATHAN VERNER
JÖRG BRENDLE
Affiliation:
GRADUATE SCHOOL OF SYSTEM INFORMATICS KOBE UNIVERSITY KOBE, JAPANE-mail:brendle@kurt.scitec.kobe-u.ac.jp
BARNABÁS FARKAS
Affiliation:
KURT GÖDEL RESEARCH CENTER UNIVERSITY OF VIENNA VIENNA, AUSTRIAE-mail:barnabasfarkas@gmail.com
JONATHAN VERNER
Affiliation:
DEPARTMENT OF LOGIC CHARLES UNIVERSITY PRAGUE, CZECH REPUBLICE-mail:jonathan.verner@matfyz.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate which filters on ω can contain towers, that is, a modulo finite descending sequence without any pseudointersection (in 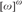${[\omega ]^\omega }$). We prove the following results:

  1. (1) Many classical examples of nice tall filters contain no towers (in ZFC).

  2. (2) It is consistent that tall analytic P-filters contain towers of arbitrary regular height (simultaneously for many regular cardinals as well).

  3. (3) It is consistent that all towers generate nonmeager filters (this answers a question of P. Borodulin-Nadzieja and D. Chodounský), in particular (consistently) Borel filters do not contain towers.

  4. (4) The statement “Every ultrafilter contains towers.” is independent of ZFC (this improves an older result of K. Kunen, J. van Mill, and C. F. Mills).

Furthermore, we study many possible logical (non)implications between the existence of towers in filters, inequalities between cardinal invariants of filters (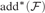${\rm{ad}}{{\rm{d}}^{\rm{*}}}\left( {\cal F} \right)$, ${\rm{co}}{{\rm{f}}^{\rm{*}}}\left( {\cal F} \right)$, 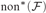${\rm{no}}{{\rm{n}}^{\rm{*}}}\left( {\cal F} \right)$, and 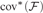${\rm{co}}{{\rm{v}}^{\rm{*}}}\left( {\cal F} \right)$), and the existence of Luzin type families (of size 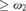$\ge {\omega _2}$), that is, if 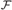${\cal F}$ is a filter then 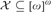${\cal X} \subseteq {[\omega ]^\omega }$ is an 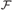${\cal F}$-Luzin family if 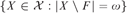$\left\{ {X \in {\cal X}:|X \setminus F| = \omega } \right\}$ is countable for every 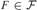$F \in {\cal F}$.

Keywords

03E0503E1703E35Borel idealanalytic idealsummable idealdensity zero idealtowerMathias–Prikry forcingLaver–Prikry forcingcardinal invariants of the continuumKatĕtov orderKatĕtov-Blass orderLuzin type familydiamondnear coherence of filters
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 3 , September 2018 , pp. 1013 - 1062
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Balcar, B., Frankiewicz, R., and Mills, C., More on nowhere dense closed P-sets. Bulletin of the Polish Academy of Sciences: Sciences Mathematiques, vol. 28 (1980), no. 5–6, pp. 295–299.Google Scholar
Balcar, B., Hernández-Hernández, F., and Hrušák, M., Combinatorics of dense subsets of the rationals. Fundamenta Mathematicae, vol. 183 (2004), pp. 59–80.CrossRefGoogle Scholar
Balcerzak, M., Farkas, B., and Gła̧b, S., Covering properties of ideals. Archive for Mathematical Logic, vol. 52 (2013), no. 3–4, pp. 279–294.CrossRefGoogle Scholar
Barbarski, P., Filipow, R., Mrożek, N., and Szuca, P., Uniform density u and Iu-covergence on a big set. Mathematical Communications, vol. 16 (2011), no. 1, pp. 125–130.Google Scholar
Bartoszyński, T., Goldstern, M., Judah, H., and Shelah, S., All meager filters may be null. Proceedings of the American Mathematical Society, vol. 117 (1993), no. 2, pp. 515–521.CrossRefGoogle Scholar
Bartoszyński, T. and Judah, H., Set Theory: On the Structure of the Real Line, A. K. Peters, Natick, MA, 1995.CrossRefGoogle Scholar
Baumgartner, J. E. and Dordal, P., Adjoining dominating functions, this JOURNAL, vol. 50 (1985), no. 1, pp. 94–101.Google Scholar
Bice, T., Filters in C*-algebras. Canadian Journal of Mathematics, vol. 65 (2013), pp. 485–509.CrossRefGoogle Scholar
Blass, A., Near coherence of filters I. Cofinal equivalence of models of arithmetic. Notre Dame Journal of Formal Logic, vol. 27 (1986), pp. 579–591.CrossRefGoogle Scholar
Blass, A., Near coherence of filters II. Applications to operator ideals, the Stone-Čech remainder of a half-line, order ideals of sequences, and slenderness of groups. Transactions of the American Mathematical Society, vol. 300 (1987), pp. 557–581.Google Scholar
Blass, A., Ultrafilters and set theory, Ultrafilters Across Mathematics (Bergelson, V., Blass, A., Di Nasso, M., and Jin, R., editors), Contemporary Mathematics, vol. 530, American Mathematical Society, Providence, RI, 2010.CrossRefGoogle Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum, Handbook of Set Theory (Foreman, M., Magidor, M., and Kanamori, A., editors), Springer-Verlag, Berlin, 2011, pp. 395–490.Google Scholar
Blass, A. and Shelah, S., Near coherence of filters III. A simplified consistency proof. Notre Dame Journal of Formal Logic, vol. 30 (1986), pp. 530–538.CrossRefGoogle Scholar
Borodulin-Nadzieja, P. and Chodounský, D., Hausdorff gaps and towers in ${\cal P}\left( \omega \right)/{\rm{Fin}}$.. Fundamenta Mathematicae, vol. 229 (2015), no. 3, pp. 197–229.CrossRefGoogle Scholar
Brendle, J., Mob families and mad families. Archive for Mathematical Logic, vol. 37 (1997), no. 3, pp. 183–197.CrossRefGoogle Scholar
Brendle, J., Shattered iteration, in preparation.Google Scholar
Brendle, J. and Flašková, J., Generic existence of ultrafilters on the natural numbers. Fundamenta Mathematicae, vol. 236 (2017), pp. 201–245.CrossRefGoogle Scholar
Brendle, J. and Hrušák, M., Countable Fréchet boolean groups: An independence result, this JOURNAL, vol. 74 (2009), no. 3, pp. 1061–1068.Google Scholar
Calbrix, J., Classes de Baire et espaces d’applications continues. Comptes Rendus de l’Académie des Sciences: Series I – Mathematics, vol. 301 (1985), pp. 759–762.Google Scholar
Calbrix, J., Filtres Boréliens sur l’ensemble des entiers et espaces d’applications continues. Revue Roumaine des Mathematiques Pures et Appliquees, vol. 33 (1988), pp. 655–661.Google Scholar
Elekes, M., A covering theorem and the random-indestructibility of the density zero ideal. Real Analysis Exchange, vol. 37 (2011–2012), no. 1, pp. 55–60.CrossRefGoogle Scholar
Engelen, F. v., On Borel ideals. Annals of Pure and Applied Logic, vol. 70, (1994), pp. 177–203.CrossRefGoogle Scholar
Farah, I., OCA and towers in ${\Cal P}\left( {\Bbb N} \right)/{\text{fin}}$.. Commentationes Mathematicae Universitatis Carolinae, vol. 37 (1996), no. 4, pp. 861–866.Google Scholar
Farah, I., Analytic Quotients: Theory of Liftings for Quotients over Analytic Ideals on the Integers, Memoirs of the American Mathematical Society, vol. 148, American Mathematical Society, Providence, RI, 2000.Google Scholar
Farkas, B., Combinatorics of Borel ideals. Ph.D. thesis, Budapest University of Technology and Economics, 2011. Available at https://repozitorium.omikk.bme.hu/bitstream/handle/10890/1137/ertekezes.pdf?sequence=1&isAllowed=y.Google Scholar
Farkas, B. and Soukup, L., More on cardinal invariants of analytic P-ideals, Commentationes Mathematicae Universitatis Carolinae, vol. 50 (2009), no. 2, pp. 281–295.Google Scholar
Farkas, B., Khomskii, Y., and Vidnyánszky, Z., Almost disjoint refinements and mixing reals. Fundamenta Mathematicae, vol. 242 (2018), pp. 25–48.CrossRefGoogle Scholar
Flašková, J., Ideals and sequentially compact spaces. Topology Proceedings, vol. 33 (2009), pp. 107–121.Google Scholar
Flašková, J., The relation of rapid ultrafilters and Q-points to Van der Waerden ideal. Acta Universitatis Carolinae. Mathematica et Physica, vol. 51 (2010), no. 4, pp. 19–27.Google Scholar
Fremlin, D. H., Measure Theory, Vol. 5, Set-Theoretic Measure Theory, Part 1, Torres Fremlin, 2008.Google Scholar
Hernández-Hernández, F., González-Hernández, C. J., and Villarreal, C. E., When is ${\Bbb R}$ the union of an increasing family of null sets? Commentationes Mathematicae Universitatis Carolinae, vol. 48 (2007), no. 4, pp. 623–630.Google Scholar
Hernández-Hernández, F. and Hrušák, M., Cardinal invariants of analytic P-ideals. Canadian Journal of Mathematics, vol. 59 (2007), no. 3, pp. 575–595.CrossRefGoogle Scholar
Hrušák, M., Combinatorics of filters and ideals. Contemporary Mathematics, vol. 533 (2011), pp. 29–69.CrossRefGoogle Scholar
Hrušák, M., Katětov order on Borel ideals, submitted.Google Scholar
Hrušák, M. and Minami, H., Mathias-Prikry and Laver-Prikry type forcing. Annals of Pure and Applied Logic, vol. 165 (2014), no. 3, pp. 880–894.CrossRefGoogle Scholar
Hrušák, M., Rojas-Rebolledo, D., and Zapletal, J., Cofinalities of Borel ideals. Mathematical Logic Quarterly, vol. 60 (2014), no. 1–2, pp. 31–39.CrossRefGoogle Scholar
Hrušák, M. and Zapletal, J., Forcing with quotients. Archive for Mathematical Logic, vol. 47 (2008), pp. 719–739.CrossRefGoogle Scholar
Jech, T., Set Theory, Springer, Berlin, 2003.Google Scholar
Judah, H. and Shelah, S., Souslin forcing, this JOURNAL, vol. 53 (1988), pp. 1188–1207.Google Scholar
Just, W., Mathias, A. R. D., Prikry, K., and Simon, P., On the existence of large p-ideals, this Journal, vol. 55 (1990), no. 2, pp. 457–465.Google Scholar
Kunen, K., van Mill, J, and Mills, C. F., On nowhere dense closed P-sets. Proceedings of the American Mathematical Society, vol. 78 (1980), no. 1, pp. 119–123.Google Scholar
Kunen, K., Medini, A., and Zdomskyy, L., Seven characterizations of non-meager P-filters. Fundamenta Mathematicae, vol. 231 (2015), no. 2, pp. 189–208.CrossRefGoogle Scholar
Malliaris, M. and Shelah, S., Cofinality spectrum theorems in model theory, set theory, and general topology. Journal of the American Mathematical Society, vol. 29 (2016), no. 1, pp. 237–297.CrossRefGoogle Scholar
Mazur, K., .${F_\sigma }$ideals and -${\omega _1}\omega _1^{\rm{*}}$gaps in the Boolean algebra .${\cal P}\left( \omega \right)/I$. Fundamenta Mathematicae , vol. 138 (1991), pp. 103–111.CrossRefGoogle Scholar
Meza-Alcántara, D., Ideals and filters on countable sets. Ph.D. thesis, Universidad Nacional Autónoma México, México, 2009.Google Scholar
Raghavan, D. and Shelah, S., Two inequalities between cardinal invariants. Fundamenta Mathematicae, vol. 237 (2017), no. 2, pp. 187–200.CrossRefGoogle Scholar
Shelah, S., Diamonds. Proceedings of the American Mathematical Society, vol. 138 (2010), pp. 2151–2161.CrossRefGoogle Scholar
Solecki, S., Analytic ideals and their applications. Annals of Pure and Applied Logic, vol. 99 (1999), 51–72.CrossRefGoogle Scholar
Solomon, R. C., Families of sets and functions. Czechoslovak Mathematical Journal, vol. 27(102) (1977), no. 4, pp. 556–559.Google Scholar
Szemerédi, E., On sets of integers containing No k elements in arithmetic progression. Acta Arithmetica, vol. 27 (1975), pp. 199–245.CrossRefGoogle Scholar
Talagrand, M., Compacts de fonctions mesurables et filtres non mesurables. Studia Mathematica, vol. 67 (1980), no. 1, pp. 13–43.CrossRefGoogle Scholar
Zafrany, S., Analytic filters and prefilters, this JOURNAL, vol. 55 (1990), no. 1, pp. 315–322.Google Scholar