Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-19T18:57:21.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Some theorems on R-maximal sets and major subsets of recursively enumerable sets

Published online by Cambridge University Press:  12 March 2014

Manuel Lerman
Manuel Lerman*
Affiliation:
Massachusetts Institute of Technology, Cambridge, Massachusetts 02139
Get access Rights & Permissions [Opens in a new window]

Extract

In [5], we studied the relational systems 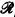/Ā obtained from the recursive functions of one variable by identifying two such functions if they are equal for all but finitely many х ∈ Ā, where Ā is an r-cohesive set. The relational systems 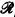/Ā with addition and multiplication defined pointwise on them, were once thought to be potential candidates for nonstandard models of arithmetic. This, however, turned out not to be the case, as was shown by Feferman, Scott, and Tennenbaum [1]. We showed, letting A and B be r-maximal sets, and letting 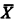denote the complement of X, that 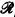/Ā and 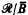are elementarily equivalent (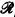/Ā ≡ 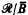) if there are r-maximal supersets C and D of A and B respectively such that C and D have the same many-one degree (C =mD). In fact, if A and B are maximal sets, 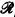/Ā ≡ 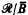if, and only if, A =mB. We wish to study the relationship between the elementary equivalence of 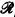/Ā and 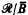, and the Turing degrees of A and B.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 36 , Issue 2 , June 1971 , pp. 193 - 215
Copyright
Copyright © Association for Symbolic Logic 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Feferman, S., Scott, D. S. and Tennenbaum, S., Models of arithmetic through function rings, 556–31, Notices of the American Mathematical Society, vol. 6 (1959), pp. 159–160.Google Scholar
[2]Friedberg, R. M., Three theorems on recursive enumeration, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[3]Kleene, S. C., Introduction to metamathematics, D. van Nostrana, Inc., New York, 1952.Google Scholar
[4]Lachlan, A. H., The lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.CrossRefGoogle Scholar
[5]Lerman, M., Recursive functions modulo co-r-maximal sets, Transactions of the American Mathematical Society, vol. 148 (1970), pp. 429–444.Google Scholar
[6]Lerman, M., Turing degrees and many-one degrees of maximal sets, this Journal, vol. 35 (1970), pp. 29–40.Google Scholar
[7]Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
[8]Robinson, R. W., Two theorems on hyperhypersimple sets, Transactions of the American Mathematical Society, vol. 128 (1967), pp. 531–538.CrossRefGoogle Scholar
[9]Sacks, G. E., Degrees of unsolvability, Annals of Mathematics Study number 55, Princeton 1963.Google Scholar