Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-23T18:13:07.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Selection in the monadic theory of a countable ordinal

Published online by Cambridge University Press:  12 March 2014

Alexander Rabinovich  and
Amit Shomrat
Alexander Rabinovich
Affiliation:
Tel-Aviv University, Sackler Faculty of Exact Sciences, Tel-Aviv 69978, Israel, E-mail: rabinoa@post.tau.ac.il
Amit Shomrat
Affiliation:
Tel-Aviv University, Sackler Faculty of Exact Sciences, Tel-Aviv 69978, Israel, E-mail: shomrata@post.tau.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

A monadic formula ψ(Y) is a selector for a formula φ(Y) in a structure 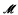if there exists a unique subset P of 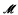which satisfies ψ and this P also satisfies φ. We show that for every ordinal α ≥ ωω there are formulas having no selector in the structure (α, <). For α ≤ ω1, we decide which formulas have a selector in (α, <) , and construct selectors for them. We deduce the impossibility of a full generalization of the Büchi-Landweber solvability theorem from (ω, <) to (ωω, <). We state a partial extension of that theorem to all countable ordinals. To each formula we assign a selection degree which measures “how difficult it is to select”. We show that in a countable ordinal all non-selectable formulas share the same degree.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 3 , September 2008 , pp. 783 - 816
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Büchi, J. R. and Landweber, L. H., Solving sequential conditions by finite-state strategies, Transactions of American Mathematical Society, vol. 138 (1969), pp. 295–311.CrossRefGoogle Scholar
[2]Büchi, J. R. and Siefkes, D., The monadic second-order theory of all countable ordinals, Decidable Theories, Vol. 2 (Büchi, J. R. and Siefkes, D., editors), Lecture Notes in Mathematics, vol. 328, Springer, 1973, pp. 1–126.CrossRefGoogle Scholar
[3]Church, A., Logic, arithmetic and automata, Proceedings of the International Congress of Mathematicians, Almquist and Wilksells, Uppsala, 1963, pp. 21–35.Google Scholar
[4]Feferman, S. and Vaught, R. L., The first-order properties of products of algebraic systems, Fundamenta Mathematical vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[5]Gurevich, Y., Monadic second-order theories, Model-Theoretic Logics (Barwise, J. and Feferman, S., editors), Springer-Verlag, 1985, pp. 479–506.Google Scholar
[6]Gurevich, Y. and Rabinovich, A., Definability in the rationals with the real order in the background, Journal of Logic and Computation, vol. 12 (2002), no. 1, pp. 1–11.CrossRefGoogle Scholar
[7]Hintikka, J., Distributive normal forms in the calculus of predicates, Acta Philosophica Fennica, vol. 6 (1953), pp. 3–71.Google Scholar
[8]Hrbacek, K. and Jech, T., Introduction to Set Theory, 3rd, revised and expanded ed., Marcel Dekker, New York, 1999.Google Scholar
[9]Larson, P. B. and Shelah, S., The stationary set splitting game, Mathematical Logic Quarterly, vol. 54 (2008), no. 2, pp. 187–193.CrossRefGoogle Scholar
[10]Läuchli, H. and Leonard, J., On the elementary theory of linear order, Fundamenta Mathematicae, vol. 59 (1966), pp. 109–116.CrossRefGoogle Scholar
[11]Lifsches, S. and Shelah, S., Uniformization and skolem functions in the class of trees, this Journal, vol. 63 (1998), no. 1, pp. 103–127.Google Scholar
[12]McNaughton, R., Testing and generating infinite sequences by a finite automaton, Information and Control, vol. 9 (1966), pp. 521–530.CrossRefGoogle Scholar
[13]Neeman, I., Finite state automata and monadic definability of ordinals, preprint. Available at: http://www.math.ucla.edu/~ineeman.Google Scholar
[14]Rabinovich, A., The Church synthesis problem over countable ordinals, submitted.Google Scholar
[15]Rabinovich, A. and Shomrat, A., Selection over classes of countable ordinals expanded by monadic predicates, submitted.Google Scholar
[16]Rosenstein, J. G., Linear Orderings, Academic Press, New York, 1982.Google Scholar
[17]Shelah, S., The monadic theory of order, Annals of Mathematics, Ser. 2, vol. 102 (1975), pp. 379–419.CrossRefGoogle Scholar
[18]Thomas, W., Ehrenfeucht games, the composition method, and the monadic theory of ordinal words, Structures in Logic and Computer Science, A Selection of Essays in Honor of A. Ehrenfeucht (Mycielski, J., Rozenberg, G., and Salomaa, A., editors), Lecture Notes in Computer Science, vol. 1261, Springer, 1997, pp. 118–143.CrossRefGoogle Scholar