Article contents
Ordinal analysis of simple cases of bar recursion
Published online by Cambridge University Press: 12 March 2014
Extract
The purpose of the following is to give an ordinal analysis of bar recursion of type 0 for the cases in which the bar recursion operator has type level 3 or 4. We show that the associated ordinals are the ε0th epsilon number and the first ε0-critical number, respectively. Also we analyze a restricted bar recursion operator of level 3 which provides the Gödel functional interpretation of an intuitionistic form of König's lemma. The ordinal in this case is ε0.
Let 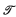 + BR0 be Gödel's theory of primitive recursive functional of finite type extended by functors Φ for bar recursion of type zero. To make bar recursion resemble transfinite recursion more closely, and thereby facilitate the ordinal analysis, we extend
+ BR0 be Gödel's theory of primitive recursive functional of finite type extended by functors Φ for bar recursion of type zero. To make bar recursion resemble transfinite recursion more closely, and thereby facilitate the ordinal analysis, we extend 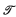 + BR0 to a system of terms
+ BR0 to a system of terms 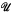 . By Theorem 1.1a term of
. By Theorem 1.1a term of 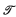 + BR0 which is computable by the rules of
+ BR0 which is computable by the rules of 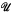 is already computable by the rules of
is already computable by the rules of 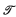 + BR0, so it is sufficient to give an ordinal analysis of the terms of
+ BR0, so it is sufficient to give an ordinal analysis of the terms of 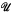 .
.
A term H of 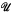 is said to be semi-closed if its free variables have level not exceeding 1. If, in addition, H has level not exceeding 2, then an ordinal measure for H is given by a length for one of its computation trees. We call this a computation size for H. Let F(X) be a term whose free variables have level not exceeding 2, and suppose the variable X of type 2 is the only free variable of level 2.
is said to be semi-closed if its free variables have level not exceeding 1. If, in addition, H has level not exceeding 2, then an ordinal measure for H is given by a length for one of its computation trees. We call this a computation size for H. Let F(X) be a term whose free variables have level not exceeding 2, and suppose the variable X of type 2 is the only free variable of level 2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 9
- Cited by




