No CrossRef data available.
Article contents
The order indiscernibles of divisible ordered abelian groups1
Published online by Cambridge University Press: 12 March 2014
Extract
There has been much work in developing the interconnections between model theory and algebra. Here we look at a particular example, the divisible ordered abelian groups, and show how the indiscernibles are related to the algebraic structure. Now a divisible ordered abelian group is a model of Th (Q, +, 0, <) and so is linearly ordered by <. Thus the theory is unstable and has a large number of models. It is therefore unrealistic to expect that a simple condition will completely determine a model. Instead we would just like to obtain nice algebraic invariants.
Definition. A subset C of a divisible ordered abelian group 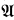 is a set of (order) indiscernibles iff for every sequence of integers n1,…,nk and for every c1 < … < ck and d1 < … < dk in C
is a set of (order) indiscernibles iff for every sequence of integers n1,…,nk and for every c1 < … < ck and d1 < … < dk in C
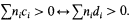
Note that this simplified form of indiscernibility is an immediate consequence of quantifier elimination for the theory. The above definition could be formulated in the language of +, 0, < but we have used subtraction as a matter of convenience. Similarly we may also use rational coefficients. Also note that a set of order indiscernibles is usually defined with respect to some external order. But in this case there are only two possibilities: the ordering inherited from 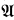 or its reverse. So we will always assume that a set of order indiscernibles has the ordering inherited from
or its reverse. So we will always assume that a set of order indiscernibles has the ordering inherited from 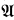 . We may sometimes refer to a set of indiscernibles as a sequence of indiscernibles if we want to explicitly mention the ordering associated with the set.
. We may sometimes refer to a set of indiscernibles as a sequence of indiscernibles if we want to explicitly mention the ordering associated with the set.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
Footnotes
The results in this paper primarily come from a chapter in the author's Ph.D. thesis [6] which was written with the valuable guidance of Professor H. J. Keisler.




