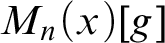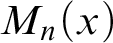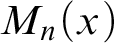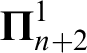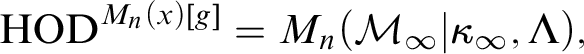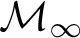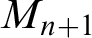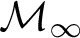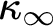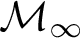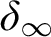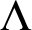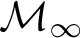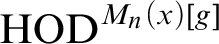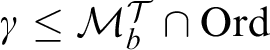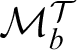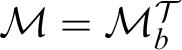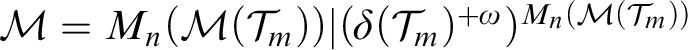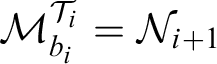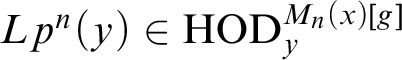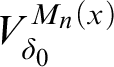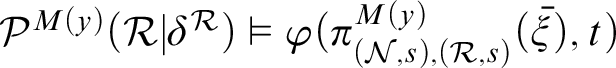1 Introduction
An essential question regarding the theory of inner models is the analysis of the class of all hereditarily ordinal definable sets
![]() $\operatorname {HOD} $
inside various inner models M of the set theoretic universe V under appropriate determinacy hypotheses. Examples for such inner models M are
$\operatorname {HOD} $
inside various inner models M of the set theoretic universe V under appropriate determinacy hypotheses. Examples for such inner models M are
![]() $L(\mathbb {R})$
,
$L(\mathbb {R})$
,
![]() $L[x]$
, and the canonical proper class x-mouse with n Woodin cardinals
$L[x]$
, and the canonical proper class x-mouse with n Woodin cardinals
![]() $M_n(x)$
, but nowadays also larger models of determinacy M are considered.
$M_n(x)$
, but nowadays also larger models of determinacy M are considered.
One motivation for analyzing the internal structure of these models
![]() $\operatorname {HOD} ^M$
is given by Woodin’s results in [Reference Koellner, Woodin, Foreman and Kanamori5] that under determinacy hypotheses these models contain large cardinals. He showed in [Reference Koellner, Woodin, Foreman and Kanamori5] for example that assuming
$\operatorname {HOD} ^M$
is given by Woodin’s results in [Reference Koellner, Woodin, Foreman and Kanamori5] that under determinacy hypotheses these models contain large cardinals. He showed in [Reference Koellner, Woodin, Foreman and Kanamori5] for example that assuming
![]() $\Delta ^1_2$
determinacy there is a Turing cone of reals x such that
$\Delta ^1_2$
determinacy there is a Turing cone of reals x such that
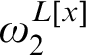 $\omega _2^{L[x]}$
is a Woodin cardinal in the model
$\omega _2^{L[x]}$
is a Woodin cardinal in the model
![]() $\operatorname {HOD} ^{L[x]}$
. This result generalizes to higher levels in the projective hierarchy. That means for
$\operatorname {HOD} ^{L[x]}$
. This result generalizes to higher levels in the projective hierarchy. That means for
![]() $n \geq 1$
assuming
$n \geq 1$
assuming
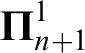 $\boldsymbol \Pi ^1_{n+1}$
determinacy and
$\boldsymbol \Pi ^1_{n+1}$
determinacy and
 $\Pi ^1_{n+2}$
determinacy there is a cone of reals x such that
$\Pi ^1_{n+2}$
determinacy there is a cone of reals x such that
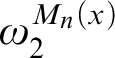 $\omega _2^{M_{n}(x)}$
is a Woodin cardinal in the model
$\omega _2^{M_{n}(x)}$
is a Woodin cardinal in the model
![]() $\operatorname {HOD} ^{M_{n}(x) | \delta _x}$
, where
$\operatorname {HOD} ^{M_{n}(x) | \delta _x}$
, where
![]() $M_{n}(x)$
denotes the canonical proper class x-mouse with n Woodin cardinals and
$M_{n}(x)$
denotes the canonical proper class x-mouse with n Woodin cardinals and
![]() $\delta _x$
is the least Woodin cardinal in
$\delta _x$
is the least Woodin cardinal in
![]() $M_{n}(x)$
. Moreover, Woodin showed a similar result for
$M_{n}(x)$
. Moreover, Woodin showed a similar result for
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
. If we let
$\operatorname {HOD} ^{L(\mathbb {R})}$
. If we let
![]() $\Theta $
denote the supremum of all ordinals
$\Theta $
denote the supremum of all ordinals
![]() $\alpha $
such that there exists a surjection
$\alpha $
such that there exists a surjection
![]() $\pi : \mathbb {R} \rightarrow \alpha $
, then assuming
$\pi : \mathbb {R} \rightarrow \alpha $
, then assuming
![]() $\operatorname {ZF} + \operatorname {AD} $
, he showed that
$\operatorname {ZF} + \operatorname {AD} $
, he showed that
![]() $\Theta ^{L(\mathbb {R})}$
is a Woodin cardinal in
$\Theta ^{L(\mathbb {R})}$
is a Woodin cardinal in
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
(see [Reference Koellner, Woodin, Foreman and Kanamori5]). The fact that these models of the form
$\operatorname {HOD} ^{L(\mathbb {R})}$
(see [Reference Koellner, Woodin, Foreman and Kanamori5]). The fact that these models of the form
![]() $\operatorname {HOD} ^M$
can have large cardinals as for example Woodin cardinals motivates the question if they are in some sense fine structural as for example the models
$\operatorname {HOD} ^M$
can have large cardinals as for example Woodin cardinals motivates the question if they are in some sense fine structural as for example the models
![]() $L[x], M_n(x)$
, and
$L[x], M_n(x)$
, and
![]() $L(\mathbb {R})$
are. A good test question for this is whether these models
$L(\mathbb {R})$
are. A good test question for this is whether these models
![]() $\operatorname {HOD} ^M$
satisfy the generalized continuum hypothesis
$\operatorname {HOD} ^M$
satisfy the generalized continuum hypothesis
![]() $\operatorname {GCH} $
. If it turns out that
$\operatorname {GCH} $
. If it turns out that
![]() $\operatorname {HOD} ^M$
is in fact a fine structural model, it would follow that it satisfies the
$\operatorname {HOD} ^M$
is in fact a fine structural model, it would follow that it satisfies the
![]() $\operatorname {GCH} $
and even stronger combinatorial principles as for example the
$\operatorname {GCH} $
and even stronger combinatorial principles as for example the
![]() $\Diamond $
principle.
$\Diamond $
principle.
The first model which was analyzed in this sense was
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
under the assumption that every set of reals in
$\operatorname {HOD} ^{L(\mathbb {R})}$
under the assumption that every set of reals in
![]() $L(\mathbb {R})$
is determined (short:
$L(\mathbb {R})$
is determined (short:
![]() $\operatorname {AD} ^{L(\mathbb {R})}$
). Using purely descriptive set theoretic methods Becker showed in [Reference Becker1] under this hypothesis that
$\operatorname {AD} ^{L(\mathbb {R})}$
). Using purely descriptive set theoretic methods Becker showed in [Reference Becker1] under this hypothesis that
![]() $\operatorname {GCH} _{\alpha }$
, i.e.,
$\operatorname {GCH} _{\alpha }$
, i.e.,
![]() $2^{\alpha } = \alpha ^+$
, holds in
$2^{\alpha } = \alpha ^+$
, holds in
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
for all
$\operatorname {HOD} ^{L(\mathbb {R})}$
for all
![]() $\alpha < \omega _1$
. Later Steel and Woodin were able to push the analysis of
$\alpha < \omega _1$
. Later Steel and Woodin were able to push the analysis of
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
forward using more recent advances in inner model theory. In 1993 they first showed independently that the reals in
$\operatorname {HOD} ^{L(\mathbb {R})}$
forward using more recent advances in inner model theory. In 1993 they first showed independently that the reals in
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
are the same as the reals in
$\operatorname {HOD} ^{L(\mathbb {R})}$
are the same as the reals in
![]() $M_{\omega }$
, the least proper class iterable premouse with
$M_{\omega }$
, the least proper class iterable premouse with
![]() $\omega $
Woodin cardinals. Then they showed in Section
$\omega $
Woodin cardinals. Then they showed in Section
![]() $4$
of [Reference Steel and Chong18] that
$4$
of [Reference Steel and Chong18] that
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
in fact agrees with the inner model N up to
$\operatorname {HOD} ^{L(\mathbb {R})}$
in fact agrees with the inner model N up to
![]() $\mathcal {P}(\omega _1)$
, where N denotes the
$\mathcal {P}(\omega _1)$
, where N denotes the
![]() $\omega _1$
-th linear iterate of
$\omega _1$
-th linear iterate of
![]() $M_{\omega }$
by its least measure and its images. Building on this, Steel was able to show in [Reference Steel, Foreman and Kanamori19] that
$M_{\omega }$
by its least measure and its images. Building on this, Steel was able to show in [Reference Steel, Foreman and Kanamori19] that
![]() $\operatorname {HOD} ^{L(\mathbb {R})}$
agrees with the inner model
$\operatorname {HOD} ^{L(\mathbb {R})}$
agrees with the inner model
![]() $\mathcal {M}_{\infty }$
up to
$\mathcal {M}_{\infty }$
up to
 $(\boldsymbol \delta _1^2)^{L(\mathbb {R})}$
, where
$(\boldsymbol \delta _1^2)^{L(\mathbb {R})}$
, where
![]() $\mathcal {M}_{\infty }$
is a direct limit of iterates of
$\mathcal {M}_{\infty }$
is a direct limit of iterates of
![]() $M_{\omega }$
and
$M_{\omega }$
and
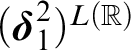 $(\boldsymbol \delta _1^2)^{L(\mathbb {R})}$
is the supremum of all ordinals
$(\boldsymbol \delta _1^2)^{L(\mathbb {R})}$
is the supremum of all ordinals
![]() $\alpha $
such that there exists a surjection
$\alpha $
such that there exists a surjection
![]() $\pi : \mathbb {R} \rightarrow \alpha $
which is
$\pi : \mathbb {R} \rightarrow \alpha $
which is
 $\boldsymbol \Delta _1^{L(\mathbb {R})}$
definable. Finally, in 1996 Woodin extended this (see [Reference Steel, Woodin, Kechris, Löwe and Steel23]) and showed that in fact
$\boldsymbol \Delta _1^{L(\mathbb {R})}$
definable. Finally, in 1996 Woodin extended this (see [Reference Steel, Woodin, Kechris, Löwe and Steel23]) and showed that in fact
 $\operatorname {HOD} ^{L(\mathbb {R})} = L[\mathcal {M}_{\infty }, \Lambda ]$
, where
$\operatorname {HOD} ^{L(\mathbb {R})} = L[\mathcal {M}_{\infty }, \Lambda ]$
, where
![]() $\Lambda $
is a partial iteration strategy for
$\Lambda $
is a partial iteration strategy for
![]() $\mathcal {M}_{\infty }$
. For even larger models of determinacy M the corresponding model
$\mathcal {M}_{\infty }$
. For even larger models of determinacy M the corresponding model
![]() $\operatorname {HOD} ^M$
was first analyzed in [Reference Sargsyan11], where the second author showed that it is fine structural using a layered hierarchy. Models of this form are nowadays called hod mice. A different approach for the fine structure of hod mice called the least branch hierarchy is studied in [Reference Steel22].
$\operatorname {HOD} ^M$
was first analyzed in [Reference Sargsyan11], where the second author showed that it is fine structural using a layered hierarchy. Models of this form are nowadays called hod mice. A different approach for the fine structure of hod mice called the least branch hierarchy is studied in [Reference Steel22].
The question if
![]() $\operatorname {HOD} ^{L[x]}$
is a model of
$\operatorname {HOD} ^{L[x]}$
is a model of
![]() $\operatorname {GCH} $
or even a fine structural model for a Turing cone of reals x under a suitable determinacy hypothesis remains open until today. What has been done is the analysis of the model
$\operatorname {GCH} $
or even a fine structural model for a Turing cone of reals x under a suitable determinacy hypothesis remains open until today. What has been done is the analysis of the model
![]() $\operatorname {HOD} ^{L[x][G]}$
, where G is
$\operatorname {HOD} ^{L[x][G]}$
, where G is
![]() $\operatorname {Col} (\omega , {<}\kappa _x)$
-generic over
$\operatorname {Col} (\omega , {<}\kappa _x)$
-generic over
![]() $\operatorname {HOD} ^{L[x]}$
for the least inaccessible cardinal
$\operatorname {HOD} ^{L[x]}$
for the least inaccessible cardinal
![]() $\kappa _x$
in
$\kappa _x$
in
![]() $L[x]$
. Woodin showed in the 1990’s (see [Reference Steel, Woodin, Kechris, Löwe and Steel23]) that assuming
$L[x]$
. Woodin showed in the 1990’s (see [Reference Steel, Woodin, Kechris, Löwe and Steel23]) that assuming
![]() $\Delta ^1_2$
determinacy there is a Turing cone of reals x such that
$\Delta ^1_2$
determinacy there is a Turing cone of reals x such that
![]() $\operatorname {HOD} ^{L[x][G]} = L[\mathcal {M}_{\infty }, \Lambda ]$
, where
$\operatorname {HOD} ^{L[x][G]} = L[\mathcal {M}_{\infty }, \Lambda ]$
, where
![]() $\mathcal {M}_{\infty }$
is a direct limit of mice (which are iterates of
$\mathcal {M}_{\infty }$
is a direct limit of mice (which are iterates of
![]() $M_1$
) and
$M_1$
) and
![]() $\Lambda $
is a partial iteration strategy for
$\Lambda $
is a partial iteration strategy for
![]() $\mathcal {M}_{\infty }$
.
$\mathcal {M}_{\infty }$
.
In this article, we analyze
![]() $\operatorname {HOD} $
in the model
$\operatorname {HOD} $
in the model
![]() $M_n(x)[g]$
for any real x of sufficiently high Turing degree under the assumption that every
$M_n(x)[g]$
for any real x of sufficiently high Turing degree under the assumption that every
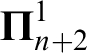 $\boldsymbol \Pi ^1_{n+2}$
set of reals is determined. Here g is
$\boldsymbol \Pi ^1_{n+2}$
set of reals is determined. Here g is
![]() $\operatorname {Col} (\omega , {<}\kappa )$
-generic over
$\operatorname {Col} (\omega , {<}\kappa )$
-generic over
![]() $M_n(x)$
, where
$M_n(x)$
, where
![]() $\kappa $
denotes the least inaccessible cardinal in
$\kappa $
denotes the least inaccessible cardinal in
![]() $M_n(x)$
. We first show that the direct limit model
$M_n(x)$
. We first show that the direct limit model
![]() $\mathcal {M}_{\infty }$
, obtained from iterates of suitable premice, agrees up to its bottom Woodin cardinal
$\mathcal {M}_{\infty }$
, obtained from iterates of suitable premice, agrees up to its bottom Woodin cardinal
![]() $\delta _{\infty }$
with
$\delta _{\infty }$
with
![]() $\operatorname {HOD} ^{M_n(x)[g]}$
. In a second step, we show that the full model
$\operatorname {HOD} ^{M_n(x)[g]}$
. In a second step, we show that the full model
![]() $\operatorname {HOD} ^{M_n(x)[g]}$
is in fact of the form
$\operatorname {HOD} ^{M_n(x)[g]}$
is in fact of the form
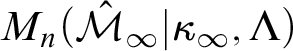 $M_n(\hat {\mathcal {M}}_{\infty } | \kappa _{\infty }, \Lambda )$
, where
$M_n(\hat {\mathcal {M}}_{\infty } | \kappa _{\infty }, \Lambda )$
, where
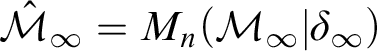 $\hat {\mathcal {M}}_{\infty } = M_n(\mathcal {M}_{\infty } | \delta _{\infty })$
,
$\hat {\mathcal {M}}_{\infty } = M_n(\mathcal {M}_{\infty } | \delta _{\infty })$
,
![]() $\kappa _{\infty }$
is the least inaccessible cardinal of
$\kappa _{\infty }$
is the least inaccessible cardinal of
![]() $\hat {\mathcal {M}}_{\infty }$
above
$\hat {\mathcal {M}}_{\infty }$
above
![]() $\delta _{\infty }$
, and
$\delta _{\infty }$
, and
![]() $\Lambda $
is a partial iteration strategy for
$\Lambda $
is a partial iteration strategy for
![]() $\mathcal {M}_{\infty }$
. Here and below
$\mathcal {M}_{\infty }$
. Here and below
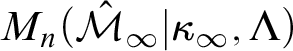 $M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
denotes the canonical fine structural model with n Woodin cardinals build over the coarse objects
$M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
denotes the canonical fine structural model with n Woodin cardinals build over the coarse objects
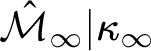 $\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
and
$\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
and
![]() $\Lambda $
. Our proof in fact shows that
$\Lambda $
. Our proof in fact shows that
![]() $\operatorname {HOD} ^{M_n(x)[g]}$
is a model of
$\operatorname {HOD} ^{M_n(x)[g]}$
is a model of
![]() $\operatorname {GCH} $
,
$\operatorname {GCH} $
,
![]() $\Diamond $
, and other combinatorial principles which are consequences of fine structure.
$\Diamond $
, and other combinatorial principles which are consequences of fine structure.
In the statement of the following main theorem and in fact everywhere in this article whenever we write
![]() $\operatorname {HOD} ^M$
for some premouse M we mean
$\operatorname {HOD} ^M$
for some premouse M we mean
![]() $\operatorname {HOD} ^{\lfloor M \rfloor }$
, where
$\operatorname {HOD} ^{\lfloor M \rfloor }$
, where
![]() $\lfloor M \rfloor $
denotes the universe of the model M. In particular, we do not allow the extender sequence of M as a parameter in the definition of
$\lfloor M \rfloor $
denotes the universe of the model M. In particular, we do not allow the extender sequence of M as a parameter in the definition of
![]() $\operatorname {HOD} $
. It will be clear from the context if we consider the model M or the universe
$\operatorname {HOD} $
. It will be clear from the context if we consider the model M or the universe
![]() $\lfloor M \rfloor $
of M, therefore we decided for the sake of readability to not distinguish the notation for these two objects.
$\lfloor M \rfloor $
of M, therefore we decided for the sake of readability to not distinguish the notation for these two objects.
The main result of this paper is the following theorem.
Theorem 1.1. Let
![]() $n < \omega $
and assume
$n < \omega $
and assume
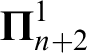 $\boldsymbol \Pi ^1_{n+2}$
-determinacy. Then for a Turing cone of reals x,
$\boldsymbol \Pi ^1_{n+2}$
-determinacy. Then for a Turing cone of reals x,
 $$\begin{align*}\operatorname{HOD} ^{M_n(x)[g]} = M_n(\hat{\mathcal{M}}_{\infty}|\kappa_{\infty}, \Lambda), \end{align*}$$
$$\begin{align*}\operatorname{HOD} ^{M_n(x)[g]} = M_n(\hat{\mathcal{M}}_{\infty}|\kappa_{\infty}, \Lambda), \end{align*}$$
where g is
![]() $\operatorname {Col} (\omega , {<}\kappa )$
-generic over
$\operatorname {Col} (\omega , {<}\kappa )$
-generic over
![]() $M_n(x)$
,
$M_n(x)$
,
![]() $\kappa $
denotes the least inaccessible cardinal in
$\kappa $
denotes the least inaccessible cardinal in
![]() $M_n(x)$
,
$M_n(x)$
,
![]() $\hat {\mathcal {M}}_{\infty }$
is a direct limit of iterates of
$\hat {\mathcal {M}}_{\infty }$
is a direct limit of iterates of
![]() $M_{n+1}$
,
$M_{n+1}$
,
![]() $\delta _{\infty }$
is the least Woodin cardinal in
$\delta _{\infty }$
is the least Woodin cardinal in
![]() $\hat {\mathcal {M}}_{\infty }$
,
$\hat {\mathcal {M}}_{\infty }$
,
![]() $\kappa _{\infty }$
is the least inaccessible cardinal of
$\kappa _{\infty }$
is the least inaccessible cardinal of
![]() $\hat {\mathcal {M}}_{\infty }$
above
$\hat {\mathcal {M}}_{\infty }$
above
![]() $\delta _{\infty }$
, and
$\delta _{\infty }$
, and
![]() $\Lambda $
is a partial iteration strategy for
$\Lambda $
is a partial iteration strategy for
![]() $\mathcal {M}_{\infty }$
.
$\mathcal {M}_{\infty }$
.
Our proof in fact shows the following corollary.
Corollary 1.2. Assume
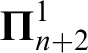 $\boldsymbol \Pi ^1_{n+2}$
-determinacy. Then for a Turing cone of reals x,
$\boldsymbol \Pi ^1_{n+2}$
-determinacy. Then for a Turing cone of reals x,
where g is
![]() $\operatorname {Col} (\omega , {<}\kappa )$
-generic over
$\operatorname {Col} (\omega , {<}\kappa )$
-generic over
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $\kappa $
denotes the least inaccessible cardinal in
$\kappa $
denotes the least inaccessible cardinal in
![]() $M_n(x)$
.
$M_n(x)$
.
Remark. In fact the full strength of
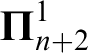 $\boldsymbol \Pi ^1_{n+2}$
-determinacy is not needed for these results. It suffices to assume that
$\boldsymbol \Pi ^1_{n+2}$
-determinacy is not needed for these results. It suffices to assume that
![]() $M_n^{\#}(x)$
exists and is
$M_n^{\#}(x)$
exists and is
![]() $\omega _1$
-iterable for all reals x (or equivalently
$\omega _1$
-iterable for all reals x (or equivalently
 $\boldsymbol \Pi ^1_{n+1}$
-determinacy, see [Reference Müller, Schindler and Woodin8] and [Reference Neeman10]) and that
$\boldsymbol \Pi ^1_{n+1}$
-determinacy, see [Reference Müller, Schindler and Woodin8] and [Reference Neeman10]) and that
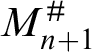 $M_{n+1}^{\#}$
exists and is
$M_{n+1}^{\#}$
exists and is
![]() $\omega _1$
-iterable. This is all we will use in the proof.
$\omega _1$
-iterable. This is all we will use in the proof.
Finally, we summarize some open questions related to these results. The following question already appears in [Reference Steel, Woodin, Kechris, Löwe and Steel23].
Question 1. Assume
![]() $\boldsymbol \Delta ^1_2$
determinacy. Is
$\boldsymbol \Delta ^1_2$
determinacy. Is
![]() $\operatorname {HOD} ^{L[x]}$
for a cone of reals x a fine structural model?
$\operatorname {HOD} ^{L[x]}$
for a cone of reals x a fine structural model?
Question 2. Assume
 $\boldsymbol \Pi ^1_{n+2}$
determinacy. Is
$\boldsymbol \Pi ^1_{n+2}$
determinacy. Is
![]() $\operatorname {HOD} ^{M_n(x)}$
for a cone of reals x a fine structural model?
$\operatorname {HOD} ^{M_n(x)}$
for a cone of reals x a fine structural model?
This article is structured as follows. In Section 2 we recall some preliminaries and fix the basic notation. In Section 3 we recall the relevant notions from [Reference Sargsyan12] and define the direct limit system converging to
![]() $\mathcal {M}_{\infty }$
, before we compute
$\mathcal {M}_{\infty }$
, before we compute
![]() $\operatorname {HOD}^{M_n(x)[g]} $
up to its Woodin cardinal in Section 4. In Section 5 we then show how this can be used to compute the full model
$\operatorname {HOD}^{M_n(x)[g]} $
up to its Woodin cardinal in Section 4. In Section 5 we then show how this can be used to compute the full model
![]() $\operatorname {HOD}^{M_n(x)[g]} $
, i.e., we finish the proof of Theorem 1.1.
$\operatorname {HOD}^{M_n(x)[g]} $
, i.e., we finish the proof of Theorem 1.1.
2 Preliminaries and notation
Whenever we say reals we mean elements of the Baire space
![]() ${}^\omega \omega $
. We also write
${}^\omega \omega $
. We also write
![]() $\mathbb {R}$
for
$\mathbb {R}$
for
![]() ${}^\omega \omega $
.
${}^\omega \omega $
.
![]() $\operatorname {HOD} $
denotes the class of all hereditarily ordinal definable sets. Moreover
$\operatorname {HOD} $
denotes the class of all hereditarily ordinal definable sets. Moreover
![]() $\operatorname {HOD} _x$
for any
$\operatorname {HOD} _x$
for any
![]() $x \in {}^\omega \omega $
denotes the class of all sets which are hereditarily ordinal definable over
$x \in {}^\omega \omega $
denotes the class of all sets which are hereditarily ordinal definable over
![]() $\{x\}$
.Footnote
1
That means we let
$\{x\}$
.Footnote
1
That means we let
![]() $A \in \operatorname {OD} _x$
iff there is a formula
$A \in \operatorname {OD} _x$
iff there is a formula
![]() $\varphi $
such that
$\varphi $
such that
![]() $A = \{ v \mid \varphi (v,\alpha _1, \dots , \alpha _n,x) \}$
for some ordinals
$A = \{ v \mid \varphi (v,\alpha _1, \dots , \alpha _n,x) \}$
for some ordinals
![]() $\alpha _1, \dots , \alpha _n$
. Then
$\alpha _1, \dots , \alpha _n$
. Then
![]() $A \in \operatorname {HOD} _x$
iff
$A \in \operatorname {HOD} _x$
iff
![]() $\operatorname {TC} (\{A\}) \subset \operatorname {OD} _x$
, where
$\operatorname {TC} (\{A\}) \subset \operatorname {OD} _x$
, where
![]() $\operatorname {TC} (\{A\})$
denotes the transitive closure of the set
$\operatorname {TC} (\{A\})$
denotes the transitive closure of the set
![]() $\{A\}$
.
$\{A\}$
.
We use the notions of premice and iterability from [Reference Steel21, Sections 1–4] and assume that the reader is familiar with the basic concepts defined there. In most cases we will demand
![]() $(\omega ,\omega _1,\omega _1)$
-iterability in the sense of Definition 4.4 in [Reference Steel21] for our mice, but in other cases or if it is not clear from the context we will state the precise amount of iterability. We say a cutpoint of a premouse
$(\omega ,\omega _1,\omega _1)$
-iterability in the sense of Definition 4.4 in [Reference Steel21] for our mice, but in other cases or if it is not clear from the context we will state the precise amount of iterability. We say a cutpoint of a premouse
![]() $\mathcal {M}$
is an infinite ordinal
$\mathcal {M}$
is an infinite ordinal
![]() $\gamma $
such that there is no extender E on the
$\gamma $
such that there is no extender E on the
![]() $\mathcal {M}$
-sequence with
$\mathcal {M}$
-sequence with
![]() $\operatorname {crit} (E) \leq \gamma \leq \operatorname {lh} (E)$
.Footnote
2
$\operatorname {crit} (E) \leq \gamma \leq \operatorname {lh} (E)$
.Footnote
2
For some
![]() $\operatorname {ZFC} $
model M and some real
$\operatorname {ZFC} $
model M and some real
![]() $x \in M$
we write
$x \in M$
we write
![]() $L[E](x)^M$
for the result of a fully backgrounded extender construction above x inside M in the sense of [Reference Mitchell and Steel7], with the minimality condition relaxed to
$L[E](x)^M$
for the result of a fully backgrounded extender construction above x inside M in the sense of [Reference Mitchell and Steel7], with the minimality condition relaxed to
![]() $\omega $
-small premice. Moreover, we let for a premouse
$\omega $
-small premice. Moreover, we let for a premouse
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $\mathcal {M} \vDash \operatorname {ZFC} $
, a cardinal cutpoint
$\mathcal {M} \vDash \operatorname {ZFC} $
, a cardinal cutpoint
![]() $\eta $
of
$\eta $
of
![]() $\mathcal {M}$
, and a premouse
$\mathcal {M}$
, and a premouse
![]() $\mathcal {N}$
of height
$\mathcal {N}$
of height
![]() $\eta $
such that
$\eta $
such that
![]() $\mathcal {N} \in \mathcal {P}(\mathcal {M} | \eta ) \cap \mathcal {M} | (\eta + \omega )$
,
$\mathcal {N} \in \mathcal {P}(\mathcal {M} | \eta ) \cap \mathcal {M} | (\eta + \omega )$
,
![]() $\mathcal {P}^{\mathcal {M}}(\mathcal {N})$
denote the result of a
$\mathcal {P}^{\mathcal {M}}(\mathcal {N})$
denote the result of a
![]() $\mathcal {P}$
-construction over
$\mathcal {P}$
-construction over
![]() $\mathcal {N}$
inside the model
$\mathcal {N}$
inside the model
![]() $\mathcal {M}$
in the sense of [Reference Schindler and Steel15] or [Reference Sargsyan12, Proposition 2.3 and Definition 2.4].
$\mathcal {M}$
in the sense of [Reference Schindler and Steel15] or [Reference Sargsyan12, Proposition 2.3 and Definition 2.4].
For
![]() $x \in {}^\omega \omega $
and
$x \in {}^\omega \omega $
and
![]() $n \leq \omega $
we let
$n \leq \omega $
we let
![]() $M_n^{\#}(x)$
, if it exists, denote a countable, sound,
$M_n^{\#}(x)$
, if it exists, denote a countable, sound,
![]() $\omega _1$
-iterable x-premouse which is not n-small but all of whose proper initial segments are n-small. In fact,
$\omega _1$
-iterable x-premouse which is not n-small but all of whose proper initial segments are n-small. In fact,
![]() $\omega _1$
-iterability suffices to show that such an
$\omega _1$
-iterability suffices to show that such an
![]() $M_n^{\#}(x)$
is unique. If
$M_n^{\#}(x)$
is unique. If
![]() $M_n^{\#}(x)$
exists, we let
$M_n^{\#}(x)$
exists, we let
![]() $M_n(x)$
be the proper class premouse obtained by iterating the top extender of
$M_n(x)$
be the proper class premouse obtained by iterating the top extender of
![]() $M_n^{\#}(x)$
out of the universe.
$M_n^{\#}(x)$
out of the universe.
3 The direct limit system
To show that
![]() $\operatorname {HOD}^{M_n(x)[g]} $
is a fine structural inner model, we will use an extension of the direct limit system introduced in [Reference Sargsyan12]. For the reader’s convenience we will first recall the relevant definitions and results from [Reference Sargsyan12], obtaining a direct limit system which is definable in
$\operatorname {HOD}^{M_n(x)[g]} $
is a fine structural inner model, we will use an extension of the direct limit system introduced in [Reference Sargsyan12]. For the reader’s convenience we will first recall the relevant definitions and results from [Reference Sargsyan12], obtaining a direct limit system which is definable in
![]() $M_n(x)$
. We use the chance to correct some minor errors in the presentation of that direct limit system in [Reference Sargsyan12]. Then we discuss the changes we need to make to obtain a direct limit system definable in
$M_n(x)$
. We use the chance to correct some minor errors in the presentation of that direct limit system in [Reference Sargsyan12]. Then we discuss the changes we need to make to obtain a direct limit system definable in
![]() $M_n(x)[g]$
. Another application of a similar but slightly different direct limit system as in [Reference Sargsyan12] can be found in [Reference Sargsyan and Schindler13].
$M_n(x)[g]$
. Another application of a similar but slightly different direct limit system as in [Reference Sargsyan12] can be found in [Reference Sargsyan and Schindler13].
Fix an arbitrary natural number n. Throughout the rest of this article we will assume that
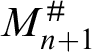 $M_{n+1}^{\#}$
exists and is
$M_{n+1}^{\#}$
exists and is
![]() $(\omega ,\omega _1,\omega _1)$
-iterable and fix a real x that codes
$(\omega ,\omega _1,\omega _1)$
-iterable and fix a real x that codes
 $M_{n+1}^{\#}$
. This implies
$M_{n+1}^{\#}$
. This implies
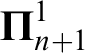 $\boldsymbol \Pi ^1_{n+1}$
determinacy or equivalently that
$\boldsymbol \Pi ^1_{n+1}$
determinacy or equivalently that
![]() $M_{n}^{\#}(z)$
exists and is
$M_{n}^{\#}(z)$
exists and is
![]() $(\omega , \omega _1, \omega _1)$
-iterable for all reals z (see [Reference Neeman9] and [Reference Müller, Schindler and Woodin8] for a proof of this equivalence due to Neeman and Woodin). Finally, we fix a
$(\omega , \omega _1, \omega _1)$
-iterable for all reals z (see [Reference Neeman9] and [Reference Müller, Schindler and Woodin8] for a proof of this equivalence due to Neeman and Woodin). Finally, we fix a
![]() $\operatorname {Col} (\omega , {<}\kappa )$
-generic g over
$\operatorname {Col} (\omega , {<}\kappa )$
-generic g over
![]() $M_n(x)$
, where
$M_n(x)$
, where
![]() $\kappa $
is the least inaccessible cardinal in
$\kappa $
is the least inaccessible cardinal in
![]() $M_n(x)$
.
$M_n(x)$
.
The first direct limit system
We first recall the definition of a lower part premouse.
Definition 3.1. Let a be a countable, transitive, self-wellorderedFootnote
3
set. Then we define the lower part model
![]() $Lp^n(a)$
as the model theoretic union of all countable a-premice
$Lp^n(a)$
as the model theoretic union of all countable a-premice
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $\rho _{\omega }(\mathcal {M}) = a$
which are n-small, sound, and
$\rho _{\omega }(\mathcal {M}) = a$
which are n-small, sound, and
![]() $(\omega , \omega _1, \omega _1)$
-iterable.
$(\omega , \omega _1, \omega _1)$
-iterable.
If
![]() $\mathcal {N}$
is a countable premouse, we also use
$\mathcal {N}$
is a countable premouse, we also use
![]() $Lp^n(\mathcal {N})$
to denote the premouse extending
$Lp^n(\mathcal {N})$
to denote the premouse extending
![]() $\mathcal {N}$
which is defined similarly as the model theoretic union of premice
$\mathcal {N}$
which is defined similarly as the model theoretic union of premice
![]() $\mathcal {M} \unrhd \mathcal {N}$
with
$\mathcal {M} \unrhd \mathcal {N}$
with
![]() $\rho _{\omega }(\mathcal {M}) \leq \mathcal {N} \cap \operatorname {Ord} $
which have
$\rho _{\omega }(\mathcal {M}) \leq \mathcal {N} \cap \operatorname {Ord} $
which have
![]() $\mathcal {N} \cap \operatorname {Ord} $
as a cutpoint, are n-small above
$\mathcal {N} \cap \operatorname {Ord} $
as a cutpoint, are n-small above
![]() $\mathcal {N} \cap \operatorname {Ord} $
, sound above
$\mathcal {N} \cap \operatorname {Ord} $
, sound above
![]() $\mathcal {N} \cap \operatorname {Ord} $
, and
$\mathcal {N} \cap \operatorname {Ord} $
, and
![]() $(\omega , \omega _1, \omega _1)$
-iterable above
$(\omega , \omega _1, \omega _1)$
-iterable above
![]() $\mathcal {N} \cap \operatorname {Ord} $
. In case
$\mathcal {N} \cap \operatorname {Ord} $
. In case
![]() $\mathcal {M} \unrhd \mathcal {N}$
has a partial measure
$\mathcal {M} \unrhd \mathcal {N}$
has a partial measure
![]() $\mu $
with critical point
$\mu $
with critical point
![]() $\mathcal {N} \cap \operatorname {Ord} $
, we replace
$\mathcal {N} \cap \operatorname {Ord} $
, we replace
![]() $\mathcal {M}$
by the corresponding translated premouse in which
$\mathcal {M}$
by the corresponding translated premouse in which
![]() $\mathcal {N} \cap \operatorname {Ord} $
is a cutpoint as in [Reference Steel20, Remark 12.7] in order to include it in
$\mathcal {N} \cap \operatorname {Ord} $
is a cutpoint as in [Reference Steel20, Remark 12.7] in order to include it in
![]() $Lp^n(\mathcal {N})$
as well.
$Lp^n(\mathcal {N})$
as well.
Definition 3.2. A countable premouse
![]() $\mathcal {N}$
is n -suitable iff there is an ordinal
$\mathcal {N}$
is n -suitable iff there is an ordinal
![]() $\delta $
such that
$\delta $
such that
-
(1)
 and
and
 $ \mathcal {N} \cap \operatorname {Ord} = \sup _{i<\omega } (\delta ^{+i})^{\mathcal {N}}$
,
$ \mathcal {N} \cap \operatorname {Ord} = \sup _{i<\omega } (\delta ^{+i})^{\mathcal {N}}$
, -
(2)
 ,
, -
(3)
 $\mathcal {N}$
is
$\mathcal {N}$
is
 $(n+1)$
-small,
$(n+1)$
-small, -
(4) for every cutpoint
 $\gamma < \delta $
of
$\gamma < \delta $
of
 $\mathcal {N}$
,
$\mathcal {N}$
,
 $\gamma $
is not Woodin in
$\gamma $
is not Woodin in
 $Lp^n(\mathcal {N}|\gamma )$
,
$Lp^n(\mathcal {N}|\gamma )$
, -
(5)
 $\mathcal {N} | (\delta ^{+(i+1)})^{\mathcal {N}} = Lp^n(\mathcal {N} | (\delta ^{+i})^{\mathcal {N}})$
for all
$\mathcal {N} | (\delta ^{+(i+1)})^{\mathcal {N}} = Lp^n(\mathcal {N} | (\delta ^{+i})^{\mathcal {N}})$
for all
 $i<\omega $
, and
$i<\omega $
, and -
(6) for all
 $\eta < \delta $
,
$\eta < \delta $
,

If
![]() $\mathcal {N}$
is an n-suitable premouse we denote the ordinal
$\mathcal {N}$
is an n-suitable premouse we denote the ordinal
![]() $\delta $
from Definition 3.2 by
$\delta $
from Definition 3.2 by
![]() $\delta ^{\mathcal {N}}$
. Moreover, we write
$\delta ^{\mathcal {N}}$
. Moreover, we write
 $\hat {\mathcal {N}} = M_n(\mathcal {N}|\delta ^{\mathcal {N}})$
for any n-suitable premouse
$\hat {\mathcal {N}} = M_n(\mathcal {N}|\delta ^{\mathcal {N}})$
for any n-suitable premouse
![]() $\mathcal {N}$
. Then
$\mathcal {N}$
. Then
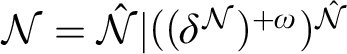 $\mathcal {N} = \hat {\mathcal {N}} | ((\delta ^{\mathcal {N}})^{+\omega })^{\hat {\mathcal {N}}}$
for every n-suitable premouse
$\mathcal {N} = \hat {\mathcal {N}} | ((\delta ^{\mathcal {N}})^{+\omega })^{\hat {\mathcal {N}}}$
for every n-suitable premouse
![]() $\mathcal {N}$
by well-known properties of the lower part model
$\mathcal {N}$
by well-known properties of the lower part model
![]() $Lp^n$
. We now give some definitions indicating how n-suitable premice can be iterated.
$Lp^n$
. We now give some definitions indicating how n-suitable premice can be iterated.
Definition 3.3. Let
![]() $\mathcal {N}$
be an arbitrary premouse and let
$\mathcal {N}$
be an arbitrary premouse and let
![]() $\mathcal {T}$
be an iteration tree on
$\mathcal {T}$
be an iteration tree on
![]() $\mathcal {N}$
of limit length.
$\mathcal {N}$
of limit length.
-
(1) We say a premouse
 $\mathcal {Q} = \mathcal {Q}(\mathcal {T})$
is a
$\mathcal {Q} = \mathcal {Q}(\mathcal {T})$
is a
 $\mathcal {Q}$
-structure for
$\mathcal {Q}$
-structure for
 $\mathcal {T}$
iff
$\mathcal {T}$
iff
 $\mathcal {M}(\mathcal {T}) \unlhd \mathcal {Q}$
,
$\mathcal {M}(\mathcal {T}) \unlhd \mathcal {Q}$
,
 $\mathcal {Q}$
is sound above
$\mathcal {Q}$
is sound above
 $\delta (\mathcal {T})$
,
$\delta (\mathcal {T})$
,
 $\delta (\mathcal {T})$
is a cutpoint of
$\delta (\mathcal {T})$
is a cutpoint of
 $\mathcal {Q}$
,
$\mathcal {Q}$
,
 $\mathcal {Q}$
is
$\mathcal {Q}$
is
 $(\omega , \omega _1, \omega _1)$
-iterable above
$(\omega , \omega _1, \omega _1)$
-iterable above
 $\delta (\mathcal {T})$
, and if
$\delta (\mathcal {T})$
, and if
 $\mathcal {Q} \neq \mathcal {M}(\mathcal {T})$
and
$\mathcal {Q} \neq \mathcal {M}(\mathcal {T})$
and
-
(i) over
 $\mathcal {Q}$
there exists an
$\mathcal {Q}$
there exists an
 $r\Sigma _n$
-definable set
$r\Sigma _n$
-definable set
 $A \subset \delta (\mathcal {T})$
such that there is no
$A \subset \delta (\mathcal {T})$
such that there is no
 $\kappa < \delta (\mathcal {T})$
such that
$\kappa < \delta (\mathcal {T})$
such that
 $\kappa $
is strong up to
$\kappa $
is strong up to
 $\delta (\mathcal {T})$
with respect to A as being witnessed by extenders on the sequence of
$\delta (\mathcal {T})$
with respect to A as being witnessed by extenders on the sequence of
 $\mathcal {Q}$
for some
$\mathcal {Q}$
for some
 $n < \omega $
, or
$n < \omega $
, or -
(ii)
 $\rho _n(\mathcal {Q}) < \delta (\mathcal {T})$
for some
$\rho _n(\mathcal {Q}) < \delta (\mathcal {T})$
for some
 $n<\omega $
.
$n<\omega $
.
-
-
(2) Let b be a cofinal well-founded branch through
 $\mathcal {T}$
. Then we say a premouse
$\mathcal {T}$
. Then we say a premouse
 $\mathcal {Q} = \mathcal {Q}(b, \mathcal {T})$
is a
$\mathcal {Q} = \mathcal {Q}(b, \mathcal {T})$
is a
 $\mathcal {Q}$
-structure for b in
$\mathcal {Q}$
-structure for b in
 $\mathcal {T}$
iff
$\mathcal {T}$
iff
 $\mathcal {Q} = \mathcal {M}_b^{\mathcal {T}} | \gamma $
, where
$\mathcal {Q} = \mathcal {M}_b^{\mathcal {T}} | \gamma $
, where
 $\gamma \leq \mathcal {M}_b^{\mathcal {T}} \cap \operatorname {Ord} $
is the least ordinal such that either or
$\gamma \leq \mathcal {M}_b^{\mathcal {T}} \cap \operatorname {Ord} $
is the least ordinal such that either or for some
for some $$\begin{align*}\gamma = \mathcal{M}_b^{\mathcal{T}} \cap \operatorname{Ord} \text{ and } \rho_n(\mathcal{M}_b^{\mathcal{T}}) < \delta(\mathcal{T}) \end{align*}$$
$$\begin{align*}\gamma = \mathcal{M}_b^{\mathcal{T}} \cap \operatorname{Ord} \text{ and } \rho_n(\mathcal{M}_b^{\mathcal{T}}) < \delta(\mathcal{T}) \end{align*}$$
 $n<\omega $
or over
$n<\omega $
or over
 $\mathcal {M}_b^{\mathcal {T}}$
there exists an
$\mathcal {M}_b^{\mathcal {T}}$
there exists an
 $r\Sigma _n$
-definable set
$r\Sigma _n$
-definable set
 $A \subset \delta (\mathcal {T})$
such that there is no
$A \subset \delta (\mathcal {T})$
such that there is no
 $\kappa < \delta (\mathcal {T})$
such that
$\kappa < \delta (\mathcal {T})$
such that
 $\kappa $
is strong up to
$\kappa $
is strong up to
 $\delta (\mathcal {T})$
with respect to A as being witnessed by extenders on the sequence of
$\delta (\mathcal {T})$
with respect to A as being witnessed by extenders on the sequence of
 $\mathcal {M}_b^{\mathcal {T}}$
for some
$\mathcal {M}_b^{\mathcal {T}}$
for some
 $n < \omega $
.
$n < \omega $
.
If no such ordinal
 $\gamma \leq \mathcal {M}_b^{\mathcal {T}} \cap \operatorname {Ord} $
exists, we let
$\gamma \leq \mathcal {M}_b^{\mathcal {T}} \cap \operatorname {Ord} $
exists, we let
 $\mathcal {Q}(b,\mathcal {T})$
be undefined.
$\mathcal {Q}(b,\mathcal {T})$
be undefined.
Remark. The premouse
![]() $M_{n+1}|(\delta _0^{+\omega })^{M_{n+1}}$
is n-suitable, where
$M_{n+1}|(\delta _0^{+\omega })^{M_{n+1}}$
is n-suitable, where
![]() $\delta _0$
is the least Woodin cardinal in
$\delta _0$
is the least Woodin cardinal in
![]() $M_{n+1}$
. We denote this premouse by
$M_{n+1}$
. We denote this premouse by
![]() $M_{n+1}^-$
and write
$M_{n+1}^-$
and write
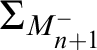 $\Sigma _{M_{n+1}^-}$
for its canonical iteration strategy induced by the usual iteration strategy
$\Sigma _{M_{n+1}^-}$
for its canonical iteration strategy induced by the usual iteration strategy
![]() $\Sigma _{M_{n+1}}$
for
$\Sigma _{M_{n+1}}$
for
![]() $M_{n+1}$
for countable stacks of normal trees without drops on the main branches.
$M_{n+1}$
for countable stacks of normal trees without drops on the main branches.
Our goal is to approximate the iteration strategy
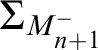 $\Sigma _{M_{n+1}^-}$
inside
$\Sigma _{M_{n+1}^-}$
inside
![]() $\operatorname {HOD}^{M_n(x)[g]} $
. Analogous to [Reference Schlutzenberg and Trang17, Definition 5.32] we define the following requirement, which will be used in Definition 3.6 to make the proof of Lemmas 3.8 and 3.9 work.
$\operatorname {HOD}^{M_n(x)[g]} $
. Analogous to [Reference Schlutzenberg and Trang17, Definition 5.32] we define the following requirement, which will be used in Definition 3.6 to make the proof of Lemmas 3.8 and 3.9 work.
Definition 3.4. Let
![]() $\mathcal {N}$
be an n-suitable premouse and let
$\mathcal {N}$
be an n-suitable premouse and let
![]() $\mathcal {T}$
be a normal iteration tree on
$\mathcal {T}$
be a normal iteration tree on
![]() $\mathcal {N}$
of length
$\mathcal {N}$
of length
![]() $< \omega _1^V$
. Then we say that
$< \omega _1^V$
. Then we say that
![]() $\mathcal {T}$
is suitability strict iff for all
$\mathcal {T}$
is suitability strict iff for all
![]() $\alpha < \operatorname {lh} (\mathcal {T})$
,
$\alpha < \operatorname {lh} (\mathcal {T})$
,
-
(i) if
 $[0, \alpha ]_T$
does not drop then
$[0, \alpha ]_T$
does not drop then
 $\mathcal {M}_{\alpha }^{\mathcal {T}}$
is n-suitable, and
$\mathcal {M}_{\alpha }^{\mathcal {T}}$
is n-suitable, and -
(ii) if
 $[0, \alpha ]_T$
drops then no
$[0, \alpha ]_T$
drops then no
 $\mathcal {R} \unlhd \mathcal {M}_{\alpha }^{\mathcal {T}}$
is n-suitable.
$\mathcal {R} \unlhd \mathcal {M}_{\alpha }^{\mathcal {T}}$
is n-suitable.
Definition 3.5. Let
![]() $\mathcal {N}$
be an n-suitable premouse and let
$\mathcal {N}$
be an n-suitable premouse and let
![]() $\mathcal {T}$
be a normal iteration tree on
$\mathcal {T}$
be a normal iteration tree on
![]() $\mathcal {N}$
of length
$\mathcal {N}$
of length
![]() $< \omega _1^V$
.
$< \omega _1^V$
.
-
(1)
 $\mathcal {T}$
is correctly guided iff for every limit ordinal
$\mathcal {T}$
is correctly guided iff for every limit ordinal
 $\lambda < \operatorname {lh} (\mathcal {T})$
, if b is the branch choosen for
$\lambda < \operatorname {lh} (\mathcal {T})$
, if b is the branch choosen for
 $\mathcal {T} \upharpoonright \lambda $
in
$\mathcal {T} \upharpoonright \lambda $
in
 $\mathcal {T}$
, then
$\mathcal {T}$
, then
 $\mathcal {Q}(b, \mathcal {T} \upharpoonright \lambda )$
exists and
$\mathcal {Q}(b, \mathcal {T} \upharpoonright \lambda )$
exists and
 $\mathcal {Q}(b, \mathcal {T} \upharpoonright \lambda ) \unlhd M_n(\mathcal {M}(\mathcal {T} \upharpoonright \lambda ))$
.
$\mathcal {Q}(b, \mathcal {T} \upharpoonright \lambda ) \unlhd M_n(\mathcal {M}(\mathcal {T} \upharpoonright \lambda ))$
. -
(2)
 $\mathcal {T}$
is short iff
$\mathcal {T}$
is short iff
 $\mathcal {T}$
is correctly guided and in case
$\mathcal {T}$
is correctly guided and in case
 $\mathcal {T}$
has limit length
$\mathcal {T}$
has limit length
 $\mathcal {Q}(\mathcal {T})$
exists and
$\mathcal {Q}(\mathcal {T})$
exists and
 $\mathcal {Q}(\mathcal {T}) \unlhd M_n(\mathcal {M}(\mathcal {T}))$
.
$\mathcal {Q}(\mathcal {T}) \unlhd M_n(\mathcal {M}(\mathcal {T}))$
. -
(3)
 $\mathcal {T}$
is maximal iff
$\mathcal {T}$
is maximal iff
 $\mathcal {T}$
is correctly guided and not short.
$\mathcal {T}$
is correctly guided and not short.
Definition 3.6. Let
![]() $\mathcal {N}$
be an n-suitable premouse. We say
$\mathcal {N}$
be an n-suitable premouse. We say
![]() $\mathcal {N}$
is short tree iterable iff whenever
$\mathcal {N}$
is short tree iterable iff whenever
![]() $\mathcal {T}$
is a short tree on
$\mathcal {T}$
is a short tree on
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
-
(i)
 $\mathcal {T}$
is suitability strict,
$\mathcal {T}$
is suitability strict, -
(ii) if
 $\mathcal {T}$
has a last model, then every putativeFootnote
4
iteration tree
$\mathcal {T}$
has a last model, then every putativeFootnote
4
iteration tree
 $\mathcal {U}$
extending
$\mathcal {U}$
extending
 $\mathcal {T}$
such that
$\mathcal {T}$
such that
 $\operatorname {lh} (\mathcal {U}) = \operatorname {lh} (\mathcal {T}) +1$
has a well-founded last model, and
$\operatorname {lh} (\mathcal {U}) = \operatorname {lh} (\mathcal {T}) +1$
has a well-founded last model, and -
(iii) if
 $\mathcal {T}$
has limit length, then there exists a cofinal well-founded branch b through
$\mathcal {T}$
has limit length, then there exists a cofinal well-founded branch b through
 $\mathcal {T}$
such that
$\mathcal {T}$
such that
 $\mathcal {Q}(b,\mathcal {T}) = \mathcal {Q}(\mathcal {T})$
.
$\mathcal {Q}(b,\mathcal {T}) = \mathcal {Q}(\mathcal {T})$
.
This can be generalized to stacks of correctly guided normal trees.
Definition 3.7. Let
![]() $\mathcal {N}$
be an n-suitable premouse and
$\mathcal {N}$
be an n-suitable premouse and
![]() $m < \omega $
. Then we say
$m < \omega $
. Then we say
![]() $(\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
is a correctly guided finite stack on
$(\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
is a correctly guided finite stack on
![]() $\mathcal {N}$
iff
$\mathcal {N}$
iff
-
(i)
 $\mathcal {N}_0 = \mathcal {N}$
,
$\mathcal {N}_0 = \mathcal {N}$
, -
(ii)
 $\mathcal {N}_i$
is n-suitable and
$\mathcal {N}_i$
is n-suitable and
 $\mathcal {T}_i$
is a correctly guided normal iteration tree on
$\mathcal {T}_i$
is a correctly guided normal iteration tree on
 $\mathcal {N}_i$
which acts below
$\mathcal {N}_i$
which acts below
 $\delta ^{\mathcal {N}_i}$
for all
$\delta ^{\mathcal {N}_i}$
for all
 $i \leq m$
, and
$i \leq m$
, and -
(iii) for every
 $i<m$
either
$i<m$
either
 $\mathcal {T}_i$
has a last model which is equal to
$\mathcal {T}_i$
has a last model which is equal to
 $\mathcal {N}_{i+1}$
and the iteration embedding
$\mathcal {N}_{i+1}$
and the iteration embedding
 $i^{\mathcal {T}_i}: \mathcal {N}_i \rightarrow \mathcal {N}_{i+1}$
exists or
$i^{\mathcal {T}_i}: \mathcal {N}_i \rightarrow \mathcal {N}_{i+1}$
exists or
 $\mathcal {T}_i$
is maximal and
$\mathcal {T}_i$
is maximal and
 $\mathcal {N}_{i+1} = M_n(\mathcal {M}(\mathcal {T}_i)) | (\delta (\mathcal {T}_i)^{+\omega })^{M_n(\mathcal {M}(\mathcal {T}_i))}$
.
$\mathcal {N}_{i+1} = M_n(\mathcal {M}(\mathcal {T}_i)) | (\delta (\mathcal {T}_i)^{+\omega })^{M_n(\mathcal {M}(\mathcal {T}_i))}$
.
Moreover, we say that
![]() $\mathcal {M}$
is the last model of
$\mathcal {M}$
is the last model of
![]() $(\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
iff either
$(\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
iff either
-
(i)
 $\mathcal {T}_m$
has a last model which is equal to
$\mathcal {T}_m$
has a last model which is equal to
 $\mathcal {M}$
and the iteration embedding
$\mathcal {M}$
and the iteration embedding
 $i^{\mathcal {T}_m}: \mathcal {N}_m \rightarrow \mathcal {M}$
exists,
$i^{\mathcal {T}_m}: \mathcal {N}_m \rightarrow \mathcal {M}$
exists, -
(ii)
 $\mathcal {T}_m$
is of limit length and short and there is a non-dropping cofinal well-founded branch b through
$\mathcal {T}_m$
is of limit length and short and there is a non-dropping cofinal well-founded branch b through
 $\mathcal {T}_m$
such that
$\mathcal {T}_m$
such that
 $\mathcal {Q}(b,\mathcal {T})$
exists,
$\mathcal {Q}(b,\mathcal {T})$
exists,
 $\mathcal {T}_m{}^\smallfrown b$
is correctly guided, and
$\mathcal {T}_m{}^\smallfrown b$
is correctly guided, and
 $\mathcal {M} = \mathcal {M}_b^{\mathcal {T}}$
, or
$\mathcal {M} = \mathcal {M}_b^{\mathcal {T}}$
, or -
(iii)
 $\mathcal {T}_m$
is maximal and
$\mathcal {T}_m$
is maximal and
 $\mathcal {M} = M_n(\mathcal {M}(\mathcal {T}_m)) | (\delta (\mathcal {T}_m)^{+\omega })^{M_n(\mathcal {M}(\mathcal {T}_m))}$
.
$\mathcal {M} = M_n(\mathcal {M}(\mathcal {T}_m)) | (\delta (\mathcal {T}_m)^{+\omega })^{M_n(\mathcal {M}(\mathcal {T}_m))}$
.
Finally, we say that
![]() $\mathcal {M}$
is a correct iterate of
$\mathcal {M}$
is a correct iterate of
![]() $\mathcal {N}$
iff there is a correctly guided finite stack on
$\mathcal {N}$
iff there is a correctly guided finite stack on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
. In case there is a correctly guided finite stack on
$\mathcal {M}$
. In case there is a correctly guided finite stack on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
of length 1, i.e., such that
$\mathcal {M}$
of length 1, i.e., such that
![]() $m=0$
, we say that
$m=0$
, we say that
![]() $\mathcal {M}$
is a pseudo-normal iterate (or just pseudo-iterate) of
$\mathcal {M}$
is a pseudo-normal iterate (or just pseudo-iterate) of
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
Analogous to Theorem 3.14 in [Reference Steel, Woodin, Kechris, Löwe and Steel23] we also have a version of the comparison lemma for short tree iterable premice and pseudo-normal iterates.
Lemma 3.8 (Pseudo-comparison lemma)
Let
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {M}$
be n-suitable premice which are short tree iterable. Then there is a common pseudo-normal iterate
$\mathcal {M}$
be n-suitable premice which are short tree iterable. Then there is a common pseudo-normal iterate
![]() $\mathcal {R} \in M_n(y)$
such that
$\mathcal {R} \in M_n(y)$
such that
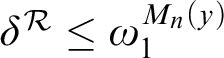 $\delta ^{\mathcal {R}} \leq \omega _1^{M_n(y)}$
, where y is a real coding
$\delta ^{\mathcal {R}} \leq \omega _1^{M_n(y)}$
, where y is a real coding
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
The proof of Lemma 3.8 is similar to the proof of Theorem 3.14 in [Reference Steel, Woodin, Kechris, Löwe and Steel23], so we omit it. Similarly, we have an analogue to the pseudo-genericity iteration (see Theorem 3.16 in [Reference Steel, Woodin, Kechris, Löwe and Steel23]).
Lemma 3.9 (Pseudo-genericity iterations)
Let
![]() $\mathcal {N}$
be an n-suitable premouse which is short tree iterable and let z be a real. Then there is a pseudo-normal iterate
$\mathcal {N}$
be an n-suitable premouse which is short tree iterable and let z be a real. Then there is a pseudo-normal iterate
![]() $\mathcal {R}$
of
$\mathcal {R}$
of
![]() $\mathcal {N}$
in
$\mathcal {N}$
in
![]() $M_n(y,z)$
such that z is
$M_n(y,z)$
such that z is
![]() $\mathbb {B}^{\mathcal {R}}$
-generic over
$\mathbb {B}^{\mathcal {R}}$
-generic over
![]() $\mathcal {R}$
and
$\mathcal {R}$
and
 $\delta ^{\mathcal {R}} \leq \omega _1^{M_n(y,z)}$
, where y is a real coding
$\delta ^{\mathcal {R}} \leq \omega _1^{M_n(y,z)}$
, where y is a real coding
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathbb {B}^{\mathcal {R}}$
denotes Woodin’s extender algebra inside
$\mathbb {B}^{\mathcal {R}}$
denotes Woodin’s extender algebra inside
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
For the definition of the direct limit system converging to
![]() $\operatorname {HOD} $
we need the notion of s-iterability. To define this, we first introduce some notation. For an n-suitable premouse
$\operatorname {HOD} $
we need the notion of s-iterability. To define this, we first introduce some notation. For an n-suitable premouse
![]() $\mathcal {N}$
, a finite sequence of ordinals s, and some
$\mathcal {N}$
, a finite sequence of ordinals s, and some
![]() $k < \omega $
let
$k < \omega $
let
 $$ \begin{align*} T_{s,k}^{\mathcal{N}} = \{ (t, \ulcorner \phi \urcorner) \in [((\delta^{\mathcal{N}})^{+k})^{\mathcal{N}}]^{<\omega} & \times \omega \mid \phi \text{ is a } \Sigma_1\text{-formula and }\\ & M_n(\mathcal{N} | \delta^{\mathcal{N}}) \vDash \phi[t,s] \}, \end{align*} $$
$$ \begin{align*} T_{s,k}^{\mathcal{N}} = \{ (t, \ulcorner \phi \urcorner) \in [((\delta^{\mathcal{N}})^{+k})^{\mathcal{N}}]^{<\omega} & \times \omega \mid \phi \text{ is a } \Sigma_1\text{-formula and }\\ & M_n(\mathcal{N} | \delta^{\mathcal{N}}) \vDash \phi[t,s] \}, \end{align*} $$
where
![]() $\ulcorner \phi \urcorner $
denotes the Gödel number of
$\ulcorner \phi \urcorner $
denotes the Gödel number of
![]() $\phi $
. Let
$\phi $
. Let
 $Hull_1^{\mathcal {N}}$
denote an uncollapsed
$Hull_1^{\mathcal {N}}$
denote an uncollapsed
![]() $\Sigma _1$
hull in
$\Sigma _1$
hull in
![]() $\mathcal {N}$
. Then we let
$\mathcal {N}$
. Then we let
 $$\begin{align*}\gamma_s^{\mathcal{N}} = \sup(Hull_1^{\mathcal{N}}(\{ T_{s,k}^{\mathcal{N}} \mid k < \omega \}) \cap \delta^{\mathcal{N}})\end{align*}$$
$$\begin{align*}\gamma_s^{\mathcal{N}} = \sup(Hull_1^{\mathcal{N}}(\{ T_{s,k}^{\mathcal{N}} \mid k < \omega \}) \cap \delta^{\mathcal{N}})\end{align*}$$
and
 $$\begin{align*}H_s^{\mathcal{N}} = Hull_1^{\mathcal{N}}( \gamma_s^{\mathcal{N}} \cup \{ T_{s,k}^{\mathcal{N}} \mid k < \omega \}). \end{align*}$$
$$\begin{align*}H_s^{\mathcal{N}} = Hull_1^{\mathcal{N}}( \gamma_s^{\mathcal{N}} \cup \{ T_{s,k}^{\mathcal{N}} \mid k < \omega \}). \end{align*}$$
Then
![]() $\gamma _s^{\mathcal {N}} = H_s^{\mathcal {N}} \cap \delta ^{\mathcal {N}}$
. For
$\gamma _s^{\mathcal {N}} = H_s^{\mathcal {N}} \cap \delta ^{\mathcal {N}}$
. For
![]() $s_m = (u_1, \dots , u_{m})$
the sequence of the first m uniform indiscernibles, we write
$s_m = (u_1, \dots , u_{m})$
the sequence of the first m uniform indiscernibles, we write
 $\gamma _m^{\mathcal {N}} = \gamma _{s_m}^{\mathcal {N}}$
and
$\gamma _m^{\mathcal {N}} = \gamma _{s_m}^{\mathcal {N}}$
and
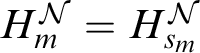 $H_m^{\mathcal {N}} = H_{s_m}^{\mathcal {N}}$
. Then we have that
$H_m^{\mathcal {N}} = H_{s_m}^{\mathcal {N}}$
. Then we have that
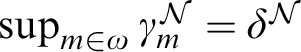 $\sup _{m \in \omega } \gamma _m^{\mathcal {N}} = \delta ^{\mathcal {N}}$
(see Lemma 5.3 in [Reference Sargsyan12]).
$\sup _{m \in \omega } \gamma _m^{\mathcal {N}} = \delta ^{\mathcal {N}}$
(see Lemma 5.3 in [Reference Sargsyan12]).
Definition 3.10. Let
![]() $\mathcal {N}$
be an n-suitable premouse and s a finite sequence of ordinals. Then
$\mathcal {N}$
be an n-suitable premouse and s a finite sequence of ordinals. Then
![]() $\mathcal {N}$
is s -iterable iff every correct iterate of
$\mathcal {N}$
is s -iterable iff every correct iterate of
![]() $\mathcal {N}$
is short tree iterable and for every correctly guided finite stack
$\mathcal {N}$
is short tree iterable and for every correctly guided finite stack
![]() $(\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
on
$(\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
there is a sequence of non-dropping branches
$\mathcal {M}$
there is a sequence of non-dropping branches
![]() $(b_i \mid i \leq m)$
and a sequence of embeddings
$(b_i \mid i \leq m)$
and a sequence of embeddings
![]() $(\pi _i \mid i \leq m)$
such that
$(\pi _i \mid i \leq m)$
such that
-
(i) if
 $\mathcal {T}_i$
has successor length
$\mathcal {T}_i$
has successor length
 $\alpha +1$
, then
$\alpha +1$
, then
 $b_i = [0,\alpha ]_{T_i}$
and
$b_i = [0,\alpha ]_{T_i}$
and
 $\pi _i = i_{0,\alpha }^{\mathcal {T}_i}$
is the corresponding iteration embedding for
$\pi _i = i_{0,\alpha }^{\mathcal {T}_i}$
is the corresponding iteration embedding for
 $i \leq m$
,
$i \leq m$
, -
(ii) if
 $\mathcal {T}_m$
is short, then
$\mathcal {T}_m$
is short, then
 $b_m$
is the unique cofinal well-founded branch through
$b_m$
is the unique cofinal well-founded branch through
 $\mathcal {T}_m$
such that
$\mathcal {T}_m$
such that
 $\mathcal {Q}(b_m,\mathcal {T}_m)$
exists and
$\mathcal {Q}(b_m,\mathcal {T}_m)$
exists and
 $\mathcal {T}_m{}^\smallfrown b_m$
is correctly guided and
$\mathcal {T}_m{}^\smallfrown b_m$
is correctly guided and
 $\pi _m = i^{\mathcal {T}_m}_{b_m}$
is the corresponding iteration embedding,
$\pi _m = i^{\mathcal {T}_m}_{b_m}$
is the corresponding iteration embedding, -
(iii) if
 $\mathcal {T}_i$
is maximal, then
$\mathcal {T}_i$
is maximal, then
 $b_i$
is a cofinal well-founded branch through
$b_i$
is a cofinal well-founded branch through
 $\mathcal {T}_i$
such that
$\mathcal {T}_i$
such that
 $\mathcal {M}_{b_i}^{\mathcal {T}_i} = \mathcal {N}_{i+1}$
if
$\mathcal {M}_{b_i}^{\mathcal {T}_i} = \mathcal {N}_{i+1}$
if
 $i<m$
or
$i<m$
or
 $\mathcal {M}_{b_i}^{\mathcal {T}_i} = \mathcal {M}$
if
$\mathcal {M}_{b_i}^{\mathcal {T}_i} = \mathcal {M}$
if
 $i =m$
, and
$i =m$
, and
 $\pi _i = i^{\mathcal {T}_i}_{b_i}$
is the corresponding iteration embedding for
$\pi _i = i^{\mathcal {T}_i}_{b_i}$
is the corresponding iteration embedding for
 $i \leq m$
, and
$i \leq m$
, and -
(iv) if we let
 $\pi = \pi _m \circ \pi _{m-1} \circ \dots \circ \pi _0$
then for every
$\pi = \pi _m \circ \pi _{m-1} \circ \dots \circ \pi _0$
then for every
 $k< \omega $
,
$k< \omega $
,  $$\begin{align*}\pi(T_{s,k}^{\mathcal{N}}) = T_{s,k}^{\mathcal{M}}.\end{align*}$$
$$\begin{align*}\pi(T_{s,k}^{\mathcal{N}}) = T_{s,k}^{\mathcal{M}}.\end{align*}$$
In this case we say that the sequence
 $\vec {b} = (b_i \mid i \leq m)$
witnesses s -iterability for
$\vec {b} = (b_i \mid i \leq m)$
witnesses s -iterability for
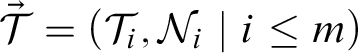 $\vec {\mathcal {T}} = (\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
or that
$\vec {\mathcal {T}} = (\mathcal {T}_i, \mathcal {N}_i \mid i \leq m)$
or that
![]() $\vec {b}$
is an s -iterability branch for
$\vec {b}$
is an s -iterability branch for
![]() $\vec {\mathcal {T}}$
and we write
$\vec {\mathcal {T}}$
and we write
![]() $\pi _{\vec {\mathcal {T}}, \vec {b}} = \pi $
.
$\pi _{\vec {\mathcal {T}}, \vec {b}} = \pi $
.
Now for every two s-iterability branches for
![]() $\vec {\mathcal {T}}$
on
$\vec {\mathcal {T}}$
on
![]() $\mathcal {N}$
their corresponding iteration embeddings agree on
$\mathcal {N}$
their corresponding iteration embeddings agree on
![]() $H_s^{\mathcal {N}}$
.
$H_s^{\mathcal {N}}$
.
Lemma 3.11 (Uniqueness of s-iterability embeddings, Lemma 5.5 in [Reference Sargsyan12])
Let
![]() $\mathcal {N}$
be an n-suitable premouse, s a finite sequence of ordinals, and
$\mathcal {N}$
be an n-suitable premouse, s a finite sequence of ordinals, and
![]() $\vec {\mathcal {T}}$
a correctly guided finite stack on
$\vec {\mathcal {T}}$
a correctly guided finite stack on
![]() $\mathcal {N}$
. Moreover let
$\mathcal {N}$
. Moreover let
![]() $\vec {b}$
and
$\vec {b}$
and
![]() $\vec {c}$
be s-iterability branches for
$\vec {c}$
be s-iterability branches for
![]() $\vec {\mathcal {T}}$
. Then
$\vec {\mathcal {T}}$
. Then
 $$\begin{align*}\pi_{\vec{\mathcal{T}}, \vec{b}} \upharpoonright H_s^{\mathcal{N}} = \pi_{\vec{\mathcal{T}}, \vec{c}} \upharpoonright H_s^{\mathcal{N}}. \end{align*}$$
$$\begin{align*}\pi_{\vec{\mathcal{T}}, \vec{b}} \upharpoonright H_s^{\mathcal{N}} = \pi_{\vec{\mathcal{T}}, \vec{c}} \upharpoonright H_s^{\mathcal{N}}. \end{align*}$$
The uniqueness of s-iterability embeddings yields that for every n-suitable, s-iterable
![]() $\mathcal {N}$
, every correctly guided finite stack
$\mathcal {N}$
, every correctly guided finite stack
![]() $\vec {\mathcal {T}}$
on
$\vec {\mathcal {T}}$
on
![]() $\mathcal {N}$
and every s-iterability branch
$\mathcal {N}$
and every s-iterability branch
![]() $\vec {b}$
for
$\vec {b}$
for
![]() $\vec {\mathcal {T}}$
, the embedding
$\vec {\mathcal {T}}$
, the embedding
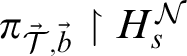 $\pi _{\vec {\mathcal {T}}, \vec {b}} \upharpoonright H_s^{\mathcal {N}}$
is independent of the choice of
$\pi _{\vec {\mathcal {T}}, \vec {b}} \upharpoonright H_s^{\mathcal {N}}$
is independent of the choice of
![]() $\vec {b}$
, but it might still depend on
$\vec {b}$
, but it might still depend on
![]() $\vec {\mathcal {T}}$
. This motivates the following definition.
$\vec {\mathcal {T}}$
. This motivates the following definition.
Definition 3.12. Let
![]() $\mathcal {N}$
be an n-suitable premouse and s a finite sequence of ordinals. Then
$\mathcal {N}$
be an n-suitable premouse and s a finite sequence of ordinals. Then
![]() $\mathcal {N}$
is strongly s -iterable iff for every correct iterate
$\mathcal {N}$
is strongly s -iterable iff for every correct iterate
![]() $\mathcal {R}$
of
$\mathcal {R}$
of
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $\mathcal {R}$
is s-iterable and for every two correctly guided finite stacks
$\mathcal {R}$
is s-iterable and for every two correctly guided finite stacks
![]() $\vec {\mathcal {T}}$
and
$\vec {\mathcal {T}}$
and
![]() $\vec {\mathcal {U}}$
on
$\vec {\mathcal {U}}$
on
![]() $\mathcal {R}$
with common last model
$\mathcal {R}$
with common last model
![]() $\mathcal {M}$
and s-iterability witnesses
$\mathcal {M}$
and s-iterability witnesses
![]() $\vec {b}$
and
$\vec {b}$
and
![]() $\vec {c}$
for
$\vec {c}$
for
![]() $\vec {\mathcal {T}}$
and
$\vec {\mathcal {T}}$
and
![]() $\vec {\mathcal {U}}$
respectively, we have that
$\vec {\mathcal {U}}$
respectively, we have that
 $$\begin{align*}\pi_{\vec{\mathcal{T}}, \vec{b}} \upharpoonright H_s^{\mathcal{R}} = \pi_{\vec{\mathcal{U}}, \vec{c}} \upharpoonright H_s^{\mathcal{R}}. \end{align*}$$
$$\begin{align*}\pi_{\vec{\mathcal{T}}, \vec{b}} \upharpoonright H_s^{\mathcal{R}} = \pi_{\vec{\mathcal{U}}, \vec{c}} \upharpoonright H_s^{\mathcal{R}}. \end{align*}$$
A so-called bad sequence argument shows the following lemma, which yields the existence of strongly s-iterable premice.
Lemma 3.13 (Lemma 5.9 in [Reference Sargsyan12])
For every finite sequence of ordinals s and any short tree iterable n-suitable premouse
![]() $\mathcal {N}$
there is a pseudo-normal iterate
$\mathcal {N}$
there is a pseudo-normal iterate
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $\mathcal {M}$
is strongly s-iterable.
$\mathcal {M}$
is strongly s-iterable.
If
![]() $\mathcal {N}$
is strongly s-iterable and
$\mathcal {N}$
is strongly s-iterable and
![]() $\vec {\mathcal {T}}$
is a correctly guided finite stack on
$\vec {\mathcal {T}}$
is a correctly guided finite stack on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
, let
$\mathcal {M}$
, let
![]() $\pi _{\mathcal {N},\mathcal {M},s} : H_s^{\mathcal {N}} \rightarrow H_s^{\mathcal {M}}$
denote the embedding given by any s-iterability branch
$\pi _{\mathcal {N},\mathcal {M},s} : H_s^{\mathcal {N}} \rightarrow H_s^{\mathcal {M}}$
denote the embedding given by any s-iterability branch
![]() $\vec {b}$
for
$\vec {b}$
for
![]() $\vec {\mathcal {T}}$
. As
$\vec {\mathcal {T}}$
. As
![]() $\mathcal {N}$
is strongly s-iterable, the embedding
$\mathcal {N}$
is strongly s-iterable, the embedding
![]() $\pi _{\mathcal {N},\mathcal {M},s}$
does not depend on the choice of
$\pi _{\mathcal {N},\mathcal {M},s}$
does not depend on the choice of
![]() $\vec {\mathcal {T}}$
and
$\vec {\mathcal {T}}$
and
![]() $\vec {b}$
.
$\vec {b}$
.
Recall that we write
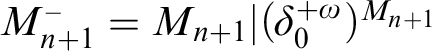 $M_{n+1}^- = M_{n+1} | (\delta _0^{+\omega })^{M_{n+1}}$
, where
$M_{n+1}^- = M_{n+1} | (\delta _0^{+\omega })^{M_{n+1}}$
, where
![]() $\delta _0$
is the least Woodin cardinal in
$\delta _0$
is the least Woodin cardinal in
![]() $M_{n+1}$
, and
$M_{n+1}$
, and
 $\Sigma _{M_{n+1}^-}$
for the canonical iteration strategy for
$\Sigma _{M_{n+1}^-}$
for the canonical iteration strategy for
![]() $M_{n+1}^-$
induced by
$M_{n+1}^-$
induced by
![]() $\Sigma _{M_{n+1}}$
. Moreover, recall that for
$\Sigma _{M_{n+1}}$
. Moreover, recall that for
![]() $m<\omega $
, we write
$m<\omega $
, we write
![]() $s_m$
for the set of the first m uniform indiscernibles. Then
$s_m$
for the set of the first m uniform indiscernibles. Then
![]() $M_{n+1}^-$
is n-suitable and strongly
$M_{n+1}^-$
is n-suitable and strongly
![]() $s_m$
-iterable for every m. Moreover, if
$s_m$
-iterable for every m. Moreover, if
![]() $\vec {\mathcal {T}}$
is a correctly guided finite stack on
$\vec {\mathcal {T}}$
is a correctly guided finite stack on
![]() $M_{n+1}^-$
with last model
$M_{n+1}^-$
with last model
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\pi _{M_{n+1}^-, \mathcal {M},s_m}$
agrees with the iteration embedding according to
$\pi _{M_{n+1}^-, \mathcal {M},s_m}$
agrees with the iteration embedding according to
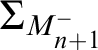 $\Sigma _{M_{n+1}^-}$
on
$\Sigma _{M_{n+1}^-}$
on
 $H_{s_m}^{M_{n+1}^-}$
. The first direct limit system we define will consist of iterates of
$H_{s_m}^{M_{n+1}^-}$
. The first direct limit system we define will consist of iterates of
![]() $M_{n+1}^-$
.
$M_{n+1}^-$
.
Definition 3.14. Let
 $$ \begin{align*} \tilde{\mathcal{F}}^{+} = \{ \mathcal{N} \mid \mathcal{N} \text{ is} & \text{ a non-dropping iterate of } M_{n+1}^- \text{ via } \Sigma_{M_{n+1}^{-}} \\ & \text{ by a finite stack of countable trees} \} \end{align*} $$
$$ \begin{align*} \tilde{\mathcal{F}}^{+} = \{ \mathcal{N} \mid \mathcal{N} \text{ is} & \text{ a non-dropping iterate of } M_{n+1}^- \text{ via } \Sigma_{M_{n+1}^{-}} \\ & \text{ by a finite stack of countable trees} \} \end{align*} $$
and for
![]() $\mathcal {N}, \mathcal {M} \in \tilde {\mathcal {F}}^+$
let
$\mathcal {N}, \mathcal {M} \in \tilde {\mathcal {F}}^+$
let
![]() $\mathcal {N} \leq ^+ \mathcal {M}$
iff
$\mathcal {N} \leq ^+ \mathcal {M}$
iff
![]() $\mathcal {M}$
is an iterate of
$\mathcal {M}$
is an iterate of
![]() $\mathcal {N}$
via the tail strategy
$\mathcal {N}$
via the tail strategy
![]() $\Sigma _{\mathcal {N}}$
as witnessed by some finite stack of countable iteration trees. Then we let
$\Sigma _{\mathcal {N}}$
as witnessed by some finite stack of countable iteration trees. Then we let
![]() $\tilde {\mathcal {M}}_{\infty }^+$
be the direct limit of
$\tilde {\mathcal {M}}_{\infty }^+$
be the direct limit of
![]() $(\tilde {\mathcal {F}}^+, \leq ^+)$
under the iteration maps.
$(\tilde {\mathcal {F}}^+, \leq ^+)$
under the iteration maps.
Remark. The prewellordering
![]() $\leq ^+$
on
$\leq ^+$
on
![]() $\tilde {\mathcal {F}}^+$
is directed and the direct limit
$\tilde {\mathcal {F}}^+$
is directed and the direct limit
![]() $\tilde {\mathcal {M}}_{\infty }^+$
is well-founded as the limit system
$\tilde {\mathcal {M}}_{\infty }^+$
is well-founded as the limit system
![]() $(\tilde {\mathcal {F}}^+, \leq ^+)$
only consists of iterates of
$(\tilde {\mathcal {F}}^+, \leq ^+)$
only consists of iterates of
![]() $M_{n+1}^-$
via the canonical iteration strategy
$M_{n+1}^-$
via the canonical iteration strategy
 $\Sigma _{M_{n+1}^-}$
.
$\Sigma _{M_{n+1}^-}$
.
Since
![]() $\tilde {\mathcal {F}}^+$
is not definable enough for our purposes, we now introduce another direct limit system which has the same direct limit
$\tilde {\mathcal {F}}^+$
is not definable enough for our purposes, we now introduce another direct limit system which has the same direct limit
![]() $\tilde {\mathcal {M}}_{\infty }^+$
.
$\tilde {\mathcal {M}}_{\infty }^+$
.
Definition 3.15. Let
 $$\begin{align*}\tilde{\mathcal{I}} = \{ (\mathcal{N}, s) \mid \mathcal{N} \text{ is } n\text{-suitable}, s \in [\operatorname{Ord} ]^{<\omega}, \text{ and } \mathcal{N} \text{ is strongly } s\text{-iterable} \} \end{align*}$$
$$\begin{align*}\tilde{\mathcal{I}} = \{ (\mathcal{N}, s) \mid \mathcal{N} \text{ is } n\text{-suitable}, s \in [\operatorname{Ord} ]^{<\omega}, \text{ and } \mathcal{N} \text{ is strongly } s\text{-iterable} \} \end{align*}$$
and
 $$\begin{align*}\tilde{\mathcal{F}} = \{ H_s^{\mathcal{N}} \mid (\mathcal{N},s) \in \tilde{\mathcal{I}} \}. \end{align*}$$
$$\begin{align*}\tilde{\mathcal{F}} = \{ H_s^{\mathcal{N}} \mid (\mathcal{N},s) \in \tilde{\mathcal{I}} \}. \end{align*}$$
For
![]() $(\mathcal {N},s), (\mathcal {M},t) \in \tilde {\mathcal {I}}$
we let
$(\mathcal {N},s), (\mathcal {M},t) \in \tilde {\mathcal {I}}$
we let
![]() $(\mathcal {N},s) \leq _{\tilde {\mathcal {I}}} (\mathcal {M},t)$
iff there is a correctly guided finite stack on
$(\mathcal {N},s) \leq _{\tilde {\mathcal {I}}} (\mathcal {M},t)$
iff there is a correctly guided finite stack on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $s \subseteq t$
. In this case we let
$s \subseteq t$
. In this case we let
 $\pi _{(\mathcal {N},s), (\mathcal {M},t)}:H_s^{\mathcal {N}} \rightarrow H_t^{\mathcal {M}}$
denote the canonical corresponding embedding.
$\pi _{(\mathcal {N},s), (\mathcal {M},t)}:H_s^{\mathcal {N}} \rightarrow H_t^{\mathcal {M}}$
denote the canonical corresponding embedding.
Remark. The prewellordering
![]() $\leq _{\tilde {\mathcal {I}}}$
on
$\leq _{\tilde {\mathcal {I}}}$
on
![]() $\tilde {\mathcal {I}}$
is directed: Let
$\tilde {\mathcal {I}}$
is directed: Let
![]() $(\mathcal {N},s), (\mathcal {M},t) \in \tilde {\mathcal {I}}$
. By Lemma 3.13 there exists an n-suitable premouse
$(\mathcal {N},s), (\mathcal {M},t) \in \tilde {\mathcal {I}}$
. By Lemma 3.13 there exists an n-suitable premouse
![]() $\mathcal {R}$
which is strongly
$\mathcal {R}$
which is strongly
![]() $(s \cup t)$
-iterable. Let
$(s \cup t)$
-iterable. Let
![]() $\mathcal {S}$
be the result of simultaneously comparing
$\mathcal {S}$
be the result of simultaneously comparing
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {R}$
in the sense of Lemma 3.8. Then
$\mathcal {R}$
in the sense of Lemma 3.8. Then
![]() $(\mathcal {S}, s \cup t) \in \tilde {\mathcal {I}}$
,
$(\mathcal {S}, s \cup t) \in \tilde {\mathcal {I}}$
,
![]() $(\mathcal {N}, s) \leq _{\tilde {\mathcal {I}}} (\mathcal {S}, s \cup t)$
, and
$(\mathcal {N}, s) \leq _{\tilde {\mathcal {I}}} (\mathcal {S}, s \cup t)$
, and
![]() $(\mathcal {M}, t) \leq _{\tilde {\mathcal {I}}} (\mathcal {S}, s \cup t)$
, as desired.
$(\mathcal {M}, t) \leq _{\tilde {\mathcal {I}}} (\mathcal {S}, s \cup t)$
, as desired.
Definition 3.16. Let
![]() $\tilde {\mathcal {M}}_{\infty }$
be the direct limit of
$\tilde {\mathcal {M}}_{\infty }$
be the direct limit of
 $(\tilde {\mathcal {F}}, \leq _{\tilde {\mathcal {I}}})$
under the embeddings
$(\tilde {\mathcal {F}}, \leq _{\tilde {\mathcal {I}}})$
under the embeddings
![]() $\pi _{(\mathcal {N},s), (\mathcal {M},t)}$
. For
$\pi _{(\mathcal {N},s), (\mathcal {M},t)}$
. For
![]() $(\mathcal {N}, s) \in \tilde {\mathcal {I}}$
let
$(\mathcal {N}, s) \in \tilde {\mathcal {I}}$
let
 $\pi _{(\mathcal {N},s),\infty } : H_s^{\mathcal {N}} \rightarrow \tilde {\mathcal {M}}_{\infty }$
denote the corresponding direct limit embedding.
$\pi _{(\mathcal {N},s),\infty } : H_s^{\mathcal {N}} \rightarrow \tilde {\mathcal {M}}_{\infty }$
denote the corresponding direct limit embedding.
The fact that
![]() $\tilde {\mathcal {M}}_{\infty }$
is well-founded follows from the next lemma.
$\tilde {\mathcal {M}}_{\infty }$
is well-founded follows from the next lemma.
Lemma 3.17 (Lemma 5.10 in [Reference Sargsyan12])
![]() $\tilde {\mathcal {M}}_{\infty } = {\tilde {\mathcal {M}}_{\infty }}^+$
.
$\tilde {\mathcal {M}}_{\infty } = {\tilde {\mathcal {M}}_{\infty }}^+$
.
The second direct limit system
To obtain
![]() $\operatorname {HOD} $
of some inner model from the direct limit, we in particular need to show that the direct limit is in fact contained in
$\operatorname {HOD} $
of some inner model from the direct limit, we in particular need to show that the direct limit is in fact contained in
![]() $\operatorname {HOD} $
of that inner model. In our setting we therefore need to internalize the direct limit system into the inner model
$\operatorname {HOD} $
of that inner model. In our setting we therefore need to internalize the direct limit system into the inner model
![]() $M_n(x)[g]$
fixed above. We first aim to define a direct limit system similar to
$M_n(x)[g]$
fixed above. We first aim to define a direct limit system similar to
 $(\tilde {\mathcal {F}}, \leq _{\tilde {\mathcal {I}}})$
in
$(\tilde {\mathcal {F}}, \leq _{\tilde {\mathcal {I}}})$
in
![]() $M_n(x)$
analogous to [Reference Sargsyan12]. In a second step, we then modify the system to obtain direct limit systems with the same direct limit which are definable in
$M_n(x)$
analogous to [Reference Sargsyan12]. In a second step, we then modify the system to obtain direct limit systems with the same direct limit which are definable in
![]() $M_n(x)[g]$
.
$M_n(x)[g]$
.
The notion of n-suitability from Definition 3.2 is already internal to
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $M_n(x)[g]$
, i.e., if
$M_n(x)[g]$
, i.e., if
![]() $\mathcal {N} \in M_n(x)|\kappa $
then
$\mathcal {N} \in M_n(x)|\kappa $
then
![]() $\mathcal {N}$
is n-suitable in V iff
$\mathcal {N}$
is n-suitable in V iff
![]() $\mathcal {N}$
is n-suitable in
$\mathcal {N}$
is n-suitable in
![]() $M_n(x)$
by the following lemma.
$M_n(x)$
by the following lemma.
Lemma 3.18. Let
![]() $\delta _0$
denote the least Woodin cardinal in
$\delta _0$
denote the least Woodin cardinal in
![]() $M_n(x)$
.
$M_n(x)$
.
-
(1) For all
 $y \in V^{M_n(x)[g]}_{\delta _0}$
,
$y \in V^{M_n(x)[g]}_{\delta _0}$
,
 $Lp^n(y) \in \operatorname {HOD} _y^{M_n(x)[g]}$
.
$Lp^n(y) \in \operatorname {HOD} _y^{M_n(x)[g]}$
. -
(2)
 $V^{M_n(x)}_{\delta _0}$
and
$V^{M_n(x)}_{\delta _0}$
and
 $V^{M_n(x)[g]}_{\delta _0}$
are closed under the operation
$V^{M_n(x)[g]}_{\delta _0}$
are closed under the operation
 $y \mapsto Lp^n(y)$
.
$y \mapsto Lp^n(y)$
.
Proof. Let
 $y \in V^{M_n(x)[g]}_{\delta _0}$
be arbitrary. The model
$y \in V^{M_n(x)[g]}_{\delta _0}$
be arbitrary. The model
![]() $M_n(x)[g]$
can be organized as a
$M_n(x)[g]$
can be organized as a
 $V_{\kappa }^{M_n(x)[g]}$
-premouse and as such it inherits the iterability from
$V_{\kappa }^{M_n(x)[g]}$
-premouse and as such it inherits the iterability from
![]() $M_n(x)$
and is in fact equal to
$M_n(x)$
and is in fact equal to
 $M_n(V_{\kappa }^{M_n(x)[g]})$
. Consider
$M_n(V_{\kappa }^{M_n(x)[g]})$
. Consider
![]() $L[E](y)^{M_n(x)[g]}$
, the result of a fully backgrounded extender construction above y using extenders from the sequence of
$L[E](y)^{M_n(x)[g]}$
, the result of a fully backgrounded extender construction above y using extenders from the sequence of
![]() $M_n(x)[g]$
organized as a
$M_n(x)[g]$
organized as a
 $V_{\kappa }^{M_n(x)[g]}$
-premouse, and compare it with
$V_{\kappa }^{M_n(x)[g]}$
-premouse, and compare it with
![]() $Lp^n(y)$
. First, we argue that
$Lp^n(y)$
. First, we argue that
![]() $Lp^n(y)$
does not move. If it would move, the
$Lp^n(y)$
does not move. If it would move, the
![]() $Lp^n(y)$
-side of the coiteration would have to drop because
$Lp^n(y)$
-side of the coiteration would have to drop because
![]() $Lp^n(y)$
does not have any total extenders. Moreover, it would have to iterate to a proper class model which is equal to an iterate of
$Lp^n(y)$
does not have any total extenders. Moreover, it would have to iterate to a proper class model which is equal to an iterate of
![]() $L[E](y)^{M_n(x)[g]}$
. As
$L[E](y)^{M_n(x)[g]}$
. As
![]() $L[E](y)^{M_n(x)[g]}$
has n Woodin cardinals, this would imply that
$L[E](y)^{M_n(x)[g]}$
has n Woodin cardinals, this would imply that
![]() $Lp^n(y)$
has a level which is not n-small, contradicting the definition of
$Lp^n(y)$
has a level which is not n-small, contradicting the definition of
![]() $Lp^n(y)$
.
$Lp^n(y)$
.
Therefore,
![]() $Lp^n(y) \lhd \mathcal {R}$
for some iterate
$Lp^n(y) \lhd \mathcal {R}$
for some iterate
![]() $\mathcal {R}$
of
$\mathcal {R}$
of
![]() $L[E](y)^{M_n(x)[g]}$
.Footnote
5
The iteration from
$L[E](y)^{M_n(x)[g]}$
.Footnote
5
The iteration from
![]() $L[E](y)^{M_n(x)[g]}$
to
$L[E](y)^{M_n(x)[g]}$
to
![]() $\mathcal {R}$
resulting from the comparison process can be defined over
$\mathcal {R}$
resulting from the comparison process can be defined over
![]() $L[E](y)^{M_n(x)[g]}$
from the extender sequence of
$L[E](y)^{M_n(x)[g]}$
from the extender sequence of
![]() $L[E](y)^{M_n(x)[g]}$
and a finite sequence of ordinals as it cannot leave any total measures behind and thus can only use measures of order 0. Let
$L[E](y)^{M_n(x)[g]}$
and a finite sequence of ordinals as it cannot leave any total measures behind and thus can only use measures of order 0. Let
 $K(V_{\kappa }^{M_n(x)[g]})^{M_n(V_{\kappa }^{M_n(x)[g]})}$
denote the core model constructed above
$K(V_{\kappa }^{M_n(x)[g]})^{M_n(V_{\kappa }^{M_n(x)[g]})}$
denote the core model constructed above
 $V_{\kappa }^{M_n(x)[g]}$
inside
$V_{\kappa }^{M_n(x)[g]}$
inside
 $M_n(V_{\kappa }^{M_n(x)[g]})$
, an n-small premouse with n Woodin cardinals, in the sense of [Reference Schindler14]. Then
$M_n(V_{\kappa }^{M_n(x)[g]})$
, an n-small premouse with n Woodin cardinals, in the sense of [Reference Schindler14]. Then
 $K(V_{\kappa }^{M_n(x)[g]})^{M_n(V_{\kappa }^{M_n(x)[g]})} = M_n(V_{\kappa }^{M_n(x)[g]})$
by [Reference Schindler14, Lemma 1.1 (due to Steel)]. Recall that the reorganization of
$K(V_{\kappa }^{M_n(x)[g]})^{M_n(V_{\kappa }^{M_n(x)[g]})} = M_n(V_{\kappa }^{M_n(x)[g]})$
by [Reference Schindler14, Lemma 1.1 (due to Steel)]. Recall that the reorganization of
![]() $M_n(x)[g]$
as a
$M_n(x)[g]$
as a
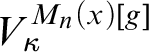 $V_{\kappa }^{M_n(x)[g]}$
-premouse is equal to
$V_{\kappa }^{M_n(x)[g]}$
-premouse is equal to
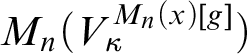 $M_n(V_{\kappa }^{M_n(x)[g]})$
. Hence, the extender sequence of the
$M_n(V_{\kappa }^{M_n(x)[g]})$
. Hence, the extender sequence of the
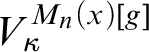 $V_{\kappa }^{M_n(x)[g]}$
-premouse
$V_{\kappa }^{M_n(x)[g]}$
-premouse
![]() $M_n(x)[g]$
is in
$M_n(x)[g]$
is in
 $\operatorname {OD} ^{M_n(x)[g]}_{V_{\kappa }^{M_n(x)[g]}} = \operatorname {OD} ^{M_n(x)[g]}$
. Therefore
$\operatorname {OD} ^{M_n(x)[g]}_{V_{\kappa }^{M_n(x)[g]}} = \operatorname {OD} ^{M_n(x)[g]}$
. Therefore
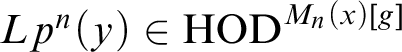 $Lp^n(y) \in \operatorname {HOD} ^{M_n(x)[g]}$
by the definability of the
$Lp^n(y) \in \operatorname {HOD} ^{M_n(x)[g]}$
by the definability of the
![]() $L[E]$
-construction.
$L[E]$
-construction.
For (2), the closure of
 $V^{M_n(x)[g]}_{\delta _0}$
follows immediately from (1). For
$V^{M_n(x)[g]}_{\delta _0}$
follows immediately from (1). For
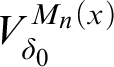 $V^{M_n(x)}_{\delta _0}$
notice that for
$V^{M_n(x)}_{\delta _0}$
notice that for
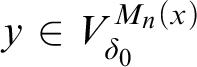 $y \in V^{M_n(x)}_{\delta _0}$
,
$y \in V^{M_n(x)}_{\delta _0}$
,
 $Lp^n(y) \in \operatorname {HOD} _y^{M_n(x)[g]} \subseteq \operatorname {HOD} _y^{M_n(x)}$
by homogeneity of the forcing.⊣
$Lp^n(y) \in \operatorname {HOD} _y^{M_n(x)[g]} \subseteq \operatorname {HOD} _y^{M_n(x)}$
by homogeneity of the forcing.⊣
By stacking the
![]() $Lp^n$
-operation, the uniform proof of Lemma 3.18 in fact shows that for all
$Lp^n$
-operation, the uniform proof of Lemma 3.18 in fact shows that for all
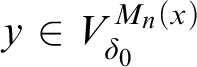 $y \in V_{\delta _0}^{M_n(x)}$
,
$y \in V_{\delta _0}^{M_n(x)}$
,
 $M_n(y)|\kappa _0 \in \operatorname {HOD}^{M_n(x)[g]} _y$
, where
$M_n(y)|\kappa _0 \in \operatorname {HOD}^{M_n(x)[g]} _y$
, where
![]() $\kappa _0$
denotes the least measurable cardinal in
$\kappa _0$
denotes the least measurable cardinal in
![]() $M_n(y)$
.
$M_n(y)$
.
The definitions of short tree, maximal tree, and correctly guided finite stack we gave above are internal to
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $M_n(x)[g]$
as well, as they can be defined only using the
$M_n(x)[g]$
as well, as they can be defined only using the
![]() $Lp^n$
-operation. The only notion we have to take care of is s-iterability since it is not even clear how the sets
$Lp^n$
-operation. The only notion we have to take care of is s-iterability since it is not even clear how the sets
 $T_{s,k}^{\mathcal {N}}$
can be identified inside
$T_{s,k}^{\mathcal {N}}$
can be identified inside
![]() $M_n(x)$
. This obstacle is solved by shrinking the direct limit system
$M_n(x)$
. This obstacle is solved by shrinking the direct limit system
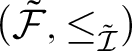 $(\tilde {\mathcal {F}}, \leq _{\tilde {\mathcal {I}}})$
to a dense subset as follows.
$(\tilde {\mathcal {F}}, \leq _{\tilde {\mathcal {I}}})$
to a dense subset as follows.
Definition 3.19. Let

See for example Section 4.1 in [Reference Fuchs, Hamkins and Reitz2] for an introduction to the
![]() $\delta $
-generator version of the extender algebra at some Woodin cardinal
$\delta $
-generator version of the extender algebra at some Woodin cardinal
![]() $\delta $
. The following lemma shows how we can use the fact that
$\delta $
. The following lemma shows how we can use the fact that
![]() $\mathcal {N} \in \mathcal {G}$
to detect
$\mathcal {N} \in \mathcal {G}$
to detect
![]() $M_n(\mathcal {N} | \delta ^{\mathcal {N}})$
inside
$M_n(\mathcal {N} | \delta ^{\mathcal {N}})$
inside
![]() $M_n(x)$
. For some premouse
$M_n(x)$
. For some premouse
![]() $\mathcal {R} \in \mathcal {G}$
we denote the last model of a
$\mathcal {R} \in \mathcal {G}$
we denote the last model of a
![]() $\mathcal {P}$
-construction above
$\mathcal {P}$
-construction above
![]() $\mathcal {R}|\delta ^{\mathcal {R}}$
performed inside
$\mathcal {R}|\delta ^{\mathcal {R}}$
performed inside
![]() $M_n(x)$
as introduced in [Reference Schindler and Steel15] (see also Proposition 2.3 and Definition 2.4 in [Reference Sargsyan12]) by
$M_n(x)$
as introduced in [Reference Schindler and Steel15] (see also Proposition 2.3 and Definition 2.4 in [Reference Sargsyan12]) by
 $\mathcal {P}^{M_n(x)}(\mathcal {R}|\delta ^{\mathcal {R}})$
.
$\mathcal {P}^{M_n(x)}(\mathcal {R}|\delta ^{\mathcal {R}})$
.
Lemma 3.20 (Lemma 5.11 in [Reference Sargsyan12])
Let
![]() $\mathcal {N} \in M_n(x)|\kappa $
be an n-suitable premouse such that for some cardinal cutpoint
$\mathcal {N} \in M_n(x)|\kappa $
be an n-suitable premouse such that for some cardinal cutpoint
![]() $\eta < \delta ^{\mathcal {N}}$
of
$\eta < \delta ^{\mathcal {N}}$
of
![]() $M_n(x)$
, we have that
$M_n(x)$
, we have that
![]() $\mathcal {N} | \delta ^{\mathcal {N}} \in \mathcal {P}(M_n(x) | \eta ^+) \cap M_n(x) | (\eta ^+ + \omega )$
and
$\mathcal {N} | \delta ^{\mathcal {N}} \in \mathcal {P}(M_n(x) | \eta ^+) \cap M_n(x) | (\eta ^+ + \omega )$
and
![]() $M_n(x) | \eta $
is generic over
$M_n(x) | \eta $
is generic over
![]() $\mathcal {N}$
for the
$\mathcal {N}$
for the
![]() $\delta ^{\mathcal {N}}$
-generator version of the extender algebra at
$\delta ^{\mathcal {N}}$
-generator version of the extender algebra at
![]() $\delta ^{\mathcal {N}}$
. Then
$\delta ^{\mathcal {N}}$
. Then
![]() $\mathcal {N} \in \mathcal {G}$
and
$\mathcal {N} \in \mathcal {G}$
and
 $$\begin{align*}\mathcal{P}^{M_n(x)}(\mathcal{N} | \delta^{\mathcal{N}}) = M_n(\mathcal{N} | \delta^{\mathcal{N}}). \end{align*}$$
$$\begin{align*}\mathcal{P}^{M_n(x)}(\mathcal{N} | \delta^{\mathcal{N}}) = M_n(\mathcal{N} | \delta^{\mathcal{N}}). \end{align*}$$
In particular,
![]() $M_n(\mathcal {N}|\delta ^{\mathcal {N}})[M_n(x)|\eta ] = M_n(x)$
.
$M_n(\mathcal {N}|\delta ^{\mathcal {N}})[M_n(x)|\eta ] = M_n(x)$
.
Using pseudo-genericity iterations (see Lemma 3.9) we can obtain the following corollary.
Corollary 3.21. Let
![]() $\mathcal {N}$
be a short tree iterable n-suitable premouse such that
$\mathcal {N}$
be a short tree iterable n-suitable premouse such that
![]() $\mathcal {N} \in M_n(x) | \kappa $
. Then there is a correctly guided finite stack on
$\mathcal {N} \in M_n(x) | \kappa $
. Then there is a correctly guided finite stack on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M} \in \mathcal {G}$
and
$\mathcal {M} \in \mathcal {G}$
and
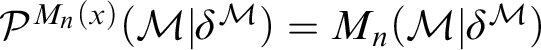 $\mathcal {P}^{M_n(x)}(\mathcal {M} | \delta ^{\mathcal {M}}) = M_n(\mathcal {M} | \delta ^{\mathcal {M}})$
.
$\mathcal {P}^{M_n(x)}(\mathcal {M} | \delta ^{\mathcal {M}}) = M_n(\mathcal {M} | \delta ^{\mathcal {M}})$
.
Now the following definition of s-iterability agrees with the previous one given in Definition 3.10 for n-suitable premice in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Definition 3.22. For
![]() $\mathcal {N} \in \mathcal {G}$
,
$\mathcal {N} \in \mathcal {G}$
,
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
, and
$s \in [\operatorname {Ord} ]^{<\omega }$
, and
![]() $k < \omega $
let
$k < \omega $
let
 $$ \begin{align*} T_{s,k}^{\mathcal{N},*} = \{ (t, \ulcorner\phi\urcorner) \in [((\delta^{\mathcal{N}})^{+k})^{\mathcal{N}}]^{<\omega} & \times \omega \mid \phi \text{ is a } \Sigma_1\text{-formula and } \\ & \mathcal{P}^{M_n(x)}(\mathcal{N} | \delta^{\mathcal{N}}) \vDash \phi[t,s] \}. \end{align*} $$
$$ \begin{align*} T_{s,k}^{\mathcal{N},*} = \{ (t, \ulcorner\phi\urcorner) \in [((\delta^{\mathcal{N}})^{+k})^{\mathcal{N}}]^{<\omega} & \times \omega \mid \phi \text{ is a } \Sigma_1\text{-formula and } \\ & \mathcal{P}^{M_n(x)}(\mathcal{N} | \delta^{\mathcal{N}}) \vDash \phi[t,s] \}. \end{align*} $$
Then we say for
![]() $\mathcal {N} \in \mathcal {G}$
and
$\mathcal {N} \in \mathcal {G}$
and
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
that
$s \in [\operatorname {Ord} ]^{<\omega }$
that
![]() $M_n(x) \vDash $
“
$M_n(x) \vDash $
“
![]() $\mathcal {N}$
is s-iterable below
$\mathcal {N}$
is s-iterable below
![]() $\kappa $
” iff for every
$\kappa $
” iff for every
![]() $\operatorname {Col} (\omega , {<}\kappa )$
-generic G over
$\operatorname {Col} (\omega , {<}\kappa )$
-generic G over
![]() $M_n(x)$
and every correctly guided finite stack
$M_n(x)$
and every correctly guided finite stack
 $\vec {\mathcal {T}} = (\mathcal {T}_i, \mathcal {N}_i \mid i \leq m) \in \operatorname {HC} ^{M_n(x)[G]}$
on
$\vec {\mathcal {T}} = (\mathcal {T}_i, \mathcal {N}_i \mid i \leq m) \in \operatorname {HC} ^{M_n(x)[G]}$
on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M} \in \mathcal {G}$
, there is a sequence of branches
$\mathcal {M} \in \mathcal {G}$
, there is a sequence of branches
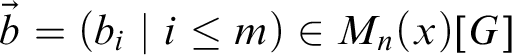 $\vec {b} = (b_i \mid i \leq m) \in M_n(x)[G]$
and a sequence of embeddings
$\vec {b} = (b_i \mid i \leq m) \in M_n(x)[G]$
and a sequence of embeddings
![]() $(\pi _i \mid i \leq m)$
satisfying
$(\pi _i \mid i \leq m)$
satisfying
![]() $(i)-(iii)$
in Definition 3.10 such that if we let
$(i)-(iii)$
in Definition 3.10 such that if we let
![]() $\pi _{\vec {\mathcal {T}},\vec {b}} = \pi _m \circ \pi _{m-1} \circ \dots \circ \pi _0$
, then for every
$\pi _{\vec {\mathcal {T}},\vec {b}} = \pi _m \circ \pi _{m-1} \circ \dots \circ \pi _0$
, then for every
![]() $k<\omega $
,
$k<\omega $
,
 $$\begin{align*}\pi_{\vec{\mathcal{T}},\vec{b}}(T_{s,k}^{\mathcal{N},*}) = T_{s,k}^{\mathcal{M},*}. \end{align*}$$
$$\begin{align*}\pi_{\vec{\mathcal{T}},\vec{b}}(T_{s,k}^{\mathcal{N},*}) = T_{s,k}^{\mathcal{M},*}. \end{align*}$$
In addition, we define
![]() $M_n(x) \vDash $
“
$M_n(x) \vDash $
“
![]() $\mathcal {N}$
is strongly s-iterable below
$\mathcal {N}$
is strongly s-iterable below
![]() $\kappa $
” analogous to Definition 3.12 for all
$\kappa $
” analogous to Definition 3.12 for all
![]() $\operatorname {Col} (\omega ,{<}\kappa )$
-generic G and stacks
$\operatorname {Col} (\omega ,{<}\kappa )$
-generic G and stacks
 $\vec {\mathcal {T}}, \vec {\mathcal {U}} \kern1.2pt{\in}\kern1.2pt M_n(x)[G]$
. For
$\vec {\mathcal {T}}, \vec {\mathcal {U}} \kern1.2pt{\in}\kern1.2pt M_n(x)[G]$
. For
![]() $\mathcal {N} \kern1.2pt{\in}\kern1.2pt \mathcal {G}$
,
$\mathcal {N} \kern1.2pt{\in}\kern1.2pt \mathcal {G}$
,
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
, and
$s \in [\operatorname {Ord} ]^{<\omega }$
, and
![]() $k < \omega $
, we have
$k < \omega $
, we have
 $T_{s,k}^{\mathcal {N},*} = T_{s,k}^{\mathcal {N}}$
, so we will omit the
$T_{s,k}^{\mathcal {N},*} = T_{s,k}^{\mathcal {N}}$
, so we will omit the
![]() $*$
for
$*$
for
![]() $\mathcal {N} \in \mathcal {G}$
. Using this,
$\mathcal {N} \in \mathcal {G}$
. Using this,
![]() $\gamma _s^{\mathcal {N}}$
and
$\gamma _s^{\mathcal {N}}$
and
![]() $H_s^{\mathcal {N}}$
are defined as before. Then we can define the internal direct limit system as follows.
$H_s^{\mathcal {N}}$
are defined as before. Then we can define the internal direct limit system as follows.
Definition 3.23. Let

and
 $$\begin{align*}\mathcal{F} = \{ H_s^{\mathcal{N}} \mid (\mathcal{N},s) \in \mathcal{I} \}. \end{align*}$$
$$\begin{align*}\mathcal{F} = \{ H_s^{\mathcal{N}} \mid (\mathcal{N},s) \in \mathcal{I} \}. \end{align*}$$
Moreover, for
![]() $(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}$
we let
$(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}$
we let
![]() $(\mathcal {N},s) \leq (\mathcal {M},t)$
iff there is a correctly guided finite stack on
$(\mathcal {N},s) \leq (\mathcal {M},t)$
iff there is a correctly guided finite stack on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $s \subseteq t$
. In this case we let as before
$s \subseteq t$
. In this case we let as before
 $\pi _{(\mathcal {N},s), (\mathcal {M},t)}:H_s^{\mathcal {N}} \rightarrow H_t^{\mathcal {M}}$
denote the canonical corresponding embedding.
$\pi _{(\mathcal {N},s), (\mathcal {M},t)}:H_s^{\mathcal {N}} \rightarrow H_t^{\mathcal {M}}$
denote the canonical corresponding embedding.
For clarity, we sometimes write
![]() $\leq _{\mathcal {I}}$
for
$\leq _{\mathcal {I}}$
for
![]() $\leq $
. Similar as before we have that for every
$\leq $
. Similar as before we have that for every
![]() $\mathcal {N} \in \mathcal {G}$
and
$\mathcal {N} \in \mathcal {G}$
and
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
there is a normal correct iterate
$s \in [\operatorname {Ord} ]^{<\omega }$
there is a normal correct iterate
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {N}$
such that
$\mathcal {N}$
such that
![]() $(\mathcal {M},s) \in \mathcal {I}$
. Using the fact that
$(\mathcal {M},s) \in \mathcal {I}$
. Using the fact that
![]() $\kappa $
is inaccessible and a limit of cutpoints in
$\kappa $
is inaccessible and a limit of cutpoints in
![]() $M_n(x)$
we can obtain the following lemma.
$M_n(x)$
we can obtain the following lemma.
Lemma 3.24 (Lemma 5.14 in [Reference Sargsyan12])
![]() $\leq $
is directed.
$\leq $
is directed.
Therefore we can again define the direct limit.
Definition 3.25. Let
![]() $\mathcal {M}_{\infty }$
be the direct limit of
$\mathcal {M}_{\infty }$
be the direct limit of
![]() $(\mathcal {F}, \leq )$
under the embeddings
$(\mathcal {F}, \leq )$
under the embeddings
![]() $\pi _{(\mathcal {N},s),(\mathcal {M},t)}$
. Moreover, let
$\pi _{(\mathcal {N},s),(\mathcal {M},t)}$
. Moreover, let
![]() $\delta _{\infty } = \delta ^{\mathcal {M}_{\infty }}$
be the Woodin cardinal in
$\delta _{\infty } = \delta ^{\mathcal {M}_{\infty }}$
be the Woodin cardinal in
![]() $\mathcal {M}_{\infty }$
and
$\mathcal {M}_{\infty }$
and
 $\pi _{(\mathcal {N},s), \infty } : H_s^{\mathcal {N}} \rightarrow \mathcal {M}_{\infty }$
be the direct limit embedding for all
$\pi _{(\mathcal {N},s), \infty } : H_s^{\mathcal {N}} \rightarrow \mathcal {M}_{\infty }$
be the direct limit embedding for all
![]() $(\mathcal {N}, s) \in \mathcal {I}$
.
$(\mathcal {N}, s) \in \mathcal {I}$
.
An argument similar to the one for Lemma 3.17 shows that this direct limit is well-founded as well. As we will use ideas from this proof in the next section, we will give some details here. We again first define another direct limit system which consists of iterates of
![]() $M_{n+1}^-$
and then show that its direct limit
$M_{n+1}^-$
and then show that its direct limit
![]() $\mathcal {M}_{\infty }^+$
is equal to
$\mathcal {M}_{\infty }^+$
is equal to
![]() $\mathcal {M}_{\infty }$
.
$\mathcal {M}_{\infty }$
.
Definition 3.26. Let
 $$ \begin{align*} \mathcal{F}^+ = \{ \mathcal{Q} \in \mathcal{G} \mid \mathcal{Q} & \text{ is the last model of a correctly guided} \\ & \text{finite stack on } M_{n+1}^- \text{ via } \Sigma_{M_{n+1}^-} \}. \end{align*} $$
$$ \begin{align*} \mathcal{F}^+ = \{ \mathcal{Q} \in \mathcal{G} \mid \mathcal{Q} & \text{ is the last model of a correctly guided} \\ & \text{finite stack on } M_{n+1}^- \text{ via } \Sigma_{M_{n+1}^-} \}. \end{align*} $$
Moreover, let
![]() $\mathcal {P} \leq ^+ \mathcal {Q}$
for
$\mathcal {P} \leq ^+ \mathcal {Q}$
for
![]() $\mathcal {P}, \mathcal {Q} \in \mathcal {F}^+$
iff there is a correctly guided finite stack on
$\mathcal {P}, \mathcal {Q} \in \mathcal {F}^+$
iff there is a correctly guided finite stack on
![]() $\mathcal {P}$
according to the tail strategy
$\mathcal {P}$
according to the tail strategy
![]() $\Sigma _{\mathcal {P}}$
with last model
$\Sigma _{\mathcal {P}}$
with last model
![]() $\mathcal {Q}$
. In this case we let
$\mathcal {Q}$
. In this case we let
![]() $i_{\mathcal {P}, \mathcal {Q}}: \mathcal {P} \rightarrow \mathcal {Q}$
denote the corresponding iteration embedding.
$i_{\mathcal {P}, \mathcal {Q}}: \mathcal {P} \rightarrow \mathcal {Q}$
denote the corresponding iteration embedding.
Then
![]() $\leq ^+$
on
$\leq ^+$
on
![]() $\mathcal {F}^+$
is directed, so we can define the direct limit.
$\mathcal {F}^+$
is directed, so we can define the direct limit.
Definition 3.27. Let
![]() $\mathcal {M}_{\infty }^+$
be the direct limit of
$\mathcal {M}_{\infty }^+$
be the direct limit of
![]() $(\mathcal {F}^+, \leq ^+)$
under the embeddings
$(\mathcal {F}^+, \leq ^+)$
under the embeddings
![]() $i_{\mathcal {P}, \mathcal {Q}}$
. Moreover, let
$i_{\mathcal {P}, \mathcal {Q}}$
. Moreover, let
![]() $i_{\mathcal {Q},\infty }: \mathcal {Q} \rightarrow \mathcal {M}_{\infty }^+$
denote the direct limit embedding for all
$i_{\mathcal {Q},\infty }: \mathcal {Q} \rightarrow \mathcal {M}_{\infty }^+$
denote the direct limit embedding for all
![]() $\mathcal {Q} \in \mathcal {F}^+$
.
$\mathcal {Q} \in \mathcal {F}^+$
.
Then it is easy to see that
![]() $\mathcal {M}_{\infty }^+$
is well-founded as
$\mathcal {M}_{\infty }^+$
is well-founded as
![]() $\mathcal {F}^+$
only consists of iterates of
$\mathcal {F}^+$
only consists of iterates of
![]() $M_{n+1}^-$
according to the canonical iteration strategy
$M_{n+1}^-$
according to the canonical iteration strategy
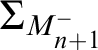 $\Sigma _{M_{n+1}^-}$
.
$\Sigma _{M_{n+1}^-}$
.
Lemma 3.28 (Lemma 5.15 in [Reference Sargsyan12])
![]() $\mathcal {M}_{\infty }^+ = \mathcal {M}_{\infty }$
and hence
$\mathcal {M}_{\infty }^+ = \mathcal {M}_{\infty }$
and hence
![]() $\mathcal {M}_{\infty }$
is well-founded.
$\mathcal {M}_{\infty }$
is well-founded.
Proof. We construct a sequence
![]() $(\mathcal {Q}_i \mid i < \omega )$
of iterates of
$(\mathcal {Q}_i \mid i < \omega )$
of iterates of
![]() $M_{n+1}^-$
such that
$M_{n+1}^-$
such that
![]() $\mathcal {Q}_i \in \mathcal {F}^+$
for every
$\mathcal {Q}_i \in \mathcal {F}^+$
for every
![]() $i < \omega $
and
$i < \omega $
and
![]() $(\mathcal {Q}_i \mid i < \omega )$
is cofinal in
$(\mathcal {Q}_i \mid i < \omega )$
is cofinal in
![]() $\mathcal {G}$
, i.e., for every
$\mathcal {G}$
, i.e., for every
![]() $\mathcal {N} \in \mathcal {G}$
there is an
$\mathcal {N} \in \mathcal {G}$
there is an
![]() $i<\omega $
such that
$i<\omega $
such that
![]() $\mathcal {Q}_i$
is the last model of a correctly guided finite stack on
$\mathcal {Q}_i$
is the last model of a correctly guided finite stack on
![]() $\mathcal {N}$
.
$\mathcal {N}$
.
In V, fix some sequence
![]() $(\xi _i \mid i < \omega )$
of ordinals cofinal in
$(\xi _i \mid i < \omega )$
of ordinals cofinal in
![]() $\kappa $
. We define
$\kappa $
. We define
![]() $(\mathcal {Q}_i \mid i < \omega )$
together with a strictly increasing sequence
$(\mathcal {Q}_i \mid i < \omega )$
together with a strictly increasing sequence
![]() $(\eta _i \mid i < \omega )$
of cardinal cutpoints of
$(\eta _i \mid i < \omega )$
of cardinal cutpoints of
![]() $M_n(x)|\kappa $
by induction on
$M_n(x)|\kappa $
by induction on
![]() $i < \omega $
. So let
$i < \omega $
. So let
![]() $\mathcal {Q}_0 = M_{n+1}^-$
and let
$\mathcal {Q}_0 = M_{n+1}^-$
and let
![]() $\eta _0 < \kappa $
be a cardinal cutpoint of
$\eta _0 < \kappa $
be a cardinal cutpoint of
![]() $M_n(x)$
. Moreover assume that we already constructed
$M_n(x)$
. Moreover assume that we already constructed
![]() $(\mathcal {Q}_i \mid i \leq j)$
and
$(\mathcal {Q}_i \mid i \leq j)$
and
![]() $(\eta _i \mid i \leq j)$
with the above mentioned properties such that in addition
$(\eta _i \mid i \leq j)$
with the above mentioned properties such that in addition
![]() $(\mathcal {Q}_i \mid i \leq j) \in M_n(x) | \eta _j$
. Let
$(\mathcal {Q}_i \mid i \leq j) \in M_n(x) | \eta _j$
. Let
![]() $\mathcal {Q}_{j+1}^*$
be the result of simultaneously pseudo-comparing (in the sense of Lemma 3.8) all n-suitable premice
$\mathcal {Q}_{j+1}^*$
be the result of simultaneously pseudo-comparing (in the sense of Lemma 3.8) all n-suitable premice
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M} \in \mathcal {G} \cap M_n(x) | \eta _j$
. Then in particular
$\mathcal {M} \in \mathcal {G} \cap M_n(x) | \eta _j$
. Then in particular
![]() $\mathcal {Q}_{j+1}^*$
is a normal iterate of
$\mathcal {Q}_{j+1}^*$
is a normal iterate of
![]() $\mathcal {Q}_{j}$
according to the canonical tail iteration strategy
$\mathcal {Q}_{j}$
according to the canonical tail iteration strategy
![]() $\Sigma _{\mathcal {Q}_j}$
, but
$\Sigma _{\mathcal {Q}_j}$
, but
![]() $\mathcal {Q}_{j+1}^*$
might not be in
$\mathcal {Q}_{j+1}^*$
might not be in
![]() $\mathcal {G}$
. Let
$\mathcal {G}$
. Let
![]() $\nu $
be a cardinal cutpoint of
$\nu $
be a cardinal cutpoint of
![]() $M_n(x)$
such that
$M_n(x)$
such that
![]() $\eta _j < \nu < \kappa $
and
$\eta _j < \nu < \kappa $
and
 $\mathcal {Q}_{j+1}^* \in M_n(x) | \nu $
. Note that such a
$\mathcal {Q}_{j+1}^* \in M_n(x) | \nu $
. Note that such a
![]() $\nu $
exists as
$\nu $
exists as
![]() $\kappa $
is inaccessible and a limit of cardinal cutpoints in
$\kappa $
is inaccessible and a limit of cardinal cutpoints in
![]() $M_n(x)$
. Let
$M_n(x)$
. Let
![]() $\mathcal {Q}_{j+1}$
be the normal iterate of
$\mathcal {Q}_{j+1}$
be the normal iterate of
![]() $\mathcal {Q}_{j+1}^*$
according to the canonical tail strategy
$\mathcal {Q}_{j+1}^*$
according to the canonical tail strategy
 $\Sigma _{\mathcal {Q}_{j+1}^*}$
of
$\Sigma _{\mathcal {Q}_{j+1}^*}$
of
![]() $\Sigma _{\mathcal {Q}_j}$
obtained by Woodin’s genericity iteration such that
$\Sigma _{\mathcal {Q}_j}$
obtained by Woodin’s genericity iteration such that
![]() $M_n(x) | \nu $
is generic over
$M_n(x) | \nu $
is generic over
![]() $\mathcal {Q}_{j+1}$
for the
$\mathcal {Q}_{j+1}$
for the
![]() $\delta ^{\mathcal {Q}_{j+1}}$
-generator version of the extender algebra (see for example Section 4.1 in [Reference Fuchs, Hamkins and Reitz2]). Then
$\delta ^{\mathcal {Q}_{j+1}}$
-generator version of the extender algebra (see for example Section 4.1 in [Reference Fuchs, Hamkins and Reitz2]). Then
![]() $\mathcal {Q}_{j+1} \in \mathcal {G}$
is as desired. Finally choose
$\mathcal {Q}_{j+1} \in \mathcal {G}$
is as desired. Finally choose
![]() $\eta _{j+1} < \kappa $
such that
$\eta _{j+1} < \kappa $
such that
![]() $\eta _{j+1}> \max (\eta _j, \xi _j)$
,
$\eta _{j+1}> \max (\eta _j, \xi _j)$
,
![]() $\eta _{j+1}$
is a cardinal cutpoint in
$\eta _{j+1}$
is a cardinal cutpoint in
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $(\mathcal {Q}_i \mid i \leq j+1) \in M_n(x) | \eta _{j+1}$
.
$(\mathcal {Q}_i \mid i \leq j+1) \in M_n(x) | \eta _{j+1}$
.
Now we define an embedding
![]() $\sigma : \mathcal {M}_{\infty } \rightarrow \mathcal {M}_{\infty }^+$
as follows. Let
$\sigma : \mathcal {M}_{\infty } \rightarrow \mathcal {M}_{\infty }^+$
as follows. Let
![]() $x \in \mathcal {M}_{\infty }$
. Since
$x \in \mathcal {M}_{\infty }$
. Since
![]() $(\mathcal {Q}_i \mid i < \omega )$
is cofinal in
$(\mathcal {Q}_i \mid i < \omega )$
is cofinal in
![]() $\mathcal {G}$
, there are
$\mathcal {G}$
, there are
![]() $i,m<\omega $
such that
$i,m<\omega $
such that
![]() $(\mathcal {Q}_i,s_m) \in \mathcal {I}$
and
$(\mathcal {Q}_i,s_m) \in \mathcal {I}$
and
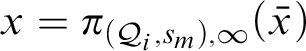 $x = \pi _{(\mathcal {Q}_i,s_m),\infty }(\bar {x})$
for some
$x = \pi _{(\mathcal {Q}_i,s_m),\infty }(\bar {x})$
for some
 $\bar {x} \in H_{s_m}^{\mathcal {Q}_i} \subseteq \mathcal {Q}_i$
. Then we let
$\bar {x} \in H_{s_m}^{\mathcal {Q}_i} \subseteq \mathcal {Q}_i$
. Then we let
![]() $\sigma (x) = i_{\mathcal {Q}_i,\infty }(\bar {x})$
.
$\sigma (x) = i_{\mathcal {Q}_i,\infty }(\bar {x})$
.
It follows as in the proof of Lemma 5.10 in [Reference Sargsyan12] that the definition of
![]() $\sigma $
does not depend on the choice of
$\sigma $
does not depend on the choice of
![]() $i,m < \omega $
and in fact
$i,m < \omega $
and in fact
![]() $\sigma = \operatorname {id}$
.⊣
$\sigma = \operatorname {id}$
.⊣
Moreover, it is possible to compute
![]() $\delta _{\infty }$
.
$\delta _{\infty }$
.
Lemma 3.29 (Lemma 5.16 in [Reference Sargsyan12])
![]() $\delta _{\infty } = (\kappa ^+)^{M_n(x)}$
.
$\delta _{\infty } = (\kappa ^+)^{M_n(x)}$
.
Direct limit systems in
 $\operatorname {HOD}^{M_n(x)[g]} $
$\operatorname {HOD}^{M_n(x)[g]} $
Finally, we will argue that
 $\mathcal {M}_{\infty } \in \operatorname {HOD}^{M_n(x)[g]} $
by first defining direct limit systems in various premice
$\mathcal {M}_{\infty } \in \operatorname {HOD}^{M_n(x)[g]} $
by first defining direct limit systems in various premice
![]() $M(y)$
satisfying certain properties definable in
$M(y)$
satisfying certain properties definable in
![]() $M_n(x)[g]$
and then showing that the direct limits
$M_n(x)[g]$
and then showing that the direct limits
 $\mathcal {M}_{\infty }^{M(y)}$
are equal to
$\mathcal {M}_{\infty }^{M(y)}$
are equal to
![]() $\mathcal {M}_{\infty }$
. A similar approach but in a completely different setting can be found in [Reference Sargsyan and Schindler13].
$\mathcal {M}_{\infty }$
. A similar approach but in a completely different setting can be found in [Reference Sargsyan and Schindler13].
In what follows, we will let
![]() $(K(z))^N$
denote the core model constructed above a real z inside some n-small model N with n Woodin cardinals in the sense of [Reference Schindler14], i.e., the core model
$(K(z))^N$
denote the core model constructed above a real z inside some n-small model N with n Woodin cardinals in the sense of [Reference Schindler14], i.e., the core model
![]() $K(z)$
is constructed between consecutive Woodin cardinals. Lemma 1.1 in [Reference Schindler14] (due to Steel) implies that
$K(z)$
is constructed between consecutive Woodin cardinals. Lemma 1.1 in [Reference Schindler14] (due to Steel) implies that
![]() $(K(x))^{M_n(x)} = M_n(x)$
. We will use this fact and consider more arbitrary premice with this property in what follows. We state the following definitions in V, but we will later apply them inside
$(K(x))^{M_n(x)} = M_n(x)$
. We will use this fact and consider more arbitrary premice with this property in what follows. We state the following definitions in V, but we will later apply them inside
![]() $M_n(x)[g]$
.
$M_n(x)[g]$
.
Definition 3.30. Let
![]() $y \in {}^\omega \omega \cap M_n(x)[g]$
. Then we say y is pre-dlm-suitable iff there is a proper class y-premouse
$y \in {}^\omega \omega \cap M_n(x)[g]$
. Then we say y is pre-dlm-suitable iff there is a proper class y-premouse
![]() $M(y)$
satisfying the following properties.
$M(y)$
satisfying the following properties.
-
(i)
 $M(y)$
is n-small and has n Woodin cardinals,
$M(y)$
is n-small and has n Woodin cardinals, -
(ii) the least inaccessible cardinal in
 $M(y)$
is
$M(y)$
is
 $\kappa $
,
$\kappa $
, -
(iii)
 $M(y) = (K(y))^{M(y)}$
, and
$M(y) = (K(y))^{M(y)}$
, and -
(iv) there is a
 $\operatorname {Col} (\omega , {<}\kappa )$
-generic h over
$\operatorname {Col} (\omega , {<}\kappa )$
-generic h over
 $M(y)$
such that
$M(y)$
such that  $$\begin{align*}M(y)[h] = M_n(x)[g]. \end{align*}$$
$$\begin{align*}M(y)[h] = M_n(x)[g]. \end{align*}$$
We also call such a y-premouse
![]() $M(y)$
pre-dlm-suitable and say that
$M(y)$
pre-dlm-suitable and say that
![]() $M(y)$
witnesses that y is pre-dlm-suitable.
$M(y)$
witnesses that y is pre-dlm-suitable.
Using this, we can define a version of the direct limit system
![]() $\mathcal {F}$
inside arbitrary pre-dlm-suitable y-premice
$\mathcal {F}$
inside arbitrary pre-dlm-suitable y-premice
![]() $M(y)$
.
$M(y)$
.
Definition 3.31. Let
![]() $y \in {}^\omega \omega $
be pre-dlm-suitable as witnessed by
$y \in {}^\omega \omega $
be pre-dlm-suitable as witnessed by
![]() $M(y)$
. Then we let
$M(y)$
. Then we let

Analogous as before, we can now define when for an n-suitable premouse
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() is strongly s-iterable below
is strongly s-iterable below
![]() $\kappa $
” by referring to
$\kappa $
” by referring to
 $\mathcal {P}^{M(y)}(\mathcal {N}|\delta ^{\mathcal {N}})$
in the definition of
$\mathcal {P}^{M(y)}(\mathcal {N}|\delta ^{\mathcal {N}})$
in the definition of
 $(T_{s,k}^{\mathcal {N},*})^{M(y)}$
. Let
$(T_{s,k}^{\mathcal {N},*})^{M(y)}$
. Let
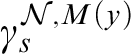 $\gamma _s^{\mathcal {N},M(y)}$
and
$\gamma _s^{\mathcal {N},M(y)}$
and
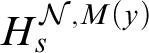 $H_s^{\mathcal {N},M(y)}$
be defined analogous to
$H_s^{\mathcal {N},M(y)}$
be defined analogous to
![]() $\gamma _s^{\mathcal {N}}$
and
$\gamma _s^{\mathcal {N}}$
and
![]() $H_s^{\mathcal {N}}$
inside
$H_s^{\mathcal {N}}$
inside
![]() $M(y)$
using
$M(y)$
using
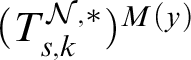 $(T_{s,k}^{\mathcal {N},*})^{M(y)}$
. For
$(T_{s,k}^{\mathcal {N},*})^{M(y)}$
. For
![]() $M(y) = M_n(x)$
and
$M(y) = M_n(x)$
and
![]() $\mathcal {N} \in \mathcal {G}$
this agrees with our previous definition of strong s-iterability.
$\mathcal {N} \in \mathcal {G}$
this agrees with our previous definition of strong s-iterability.
Definition 3.32. Let
![]() $y \in {}^\omega \omega $
be pre-dlm-suitable as witnessed by
$y \in {}^\omega \omega $
be pre-dlm-suitable as witnessed by
![]() $M(y)$
. Then we let
$M(y)$
. Then we let

and
 $$\begin{align*}\mathcal{F}^{M(y)} = \{ H_s^{\mathcal{N},M(y)} \mid (\mathcal{N},s) \in \mathcal{I}^{M(y)} \}. \end{align*}$$
$$\begin{align*}\mathcal{F}^{M(y)} = \{ H_s^{\mathcal{N},M(y)} \mid (\mathcal{N},s) \in \mathcal{I}^{M(y)} \}. \end{align*}$$
Moreover, for
![]() $(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}^{M(y)}$
we let
$(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}^{M(y)}$
we let
![]() $(\mathcal {N},s) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
iff there is a correctly guided finite stack on
$(\mathcal {N},s) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
iff there is a correctly guided finite stack on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $s \subseteq t$
. In this case we let
$s \subseteq t$
. In this case we let
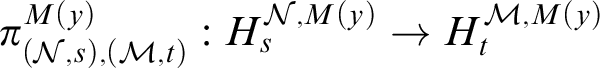 $\pi ^{M(y)}_{(\mathcal {N},s), (\mathcal {M},t)}:H_s^{\mathcal {N},M(y)} \rightarrow H_t^{\mathcal {M},M(y)}$
denote the canonical corresponding embedding. Finally, let
$\pi ^{M(y)}_{(\mathcal {N},s), (\mathcal {M},t)}:H_s^{\mathcal {N},M(y)} \rightarrow H_t^{\mathcal {M},M(y)}$
denote the canonical corresponding embedding. Finally, let
 $\mathcal {M}_{\infty }^{M(y)}$
denote the direct limit of
$\mathcal {M}_{\infty }^{M(y)}$
denote the direct limit of
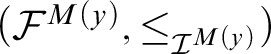 $(\mathcal {F}^{M(y)}, \leq _{\mathcal {I}^{M(y)}})$
under these embeddings.
$(\mathcal {F}^{M(y)}, \leq _{\mathcal {I}^{M(y)}})$
under these embeddings.
We will now strengthen this and define when a real
![]() $y \in {}^\omega \omega $
(or a y-premouse
$y \in {}^\omega \omega $
(or a y-premouse
![]() $M(y)$
) is dlm-suitable.
$M(y)$
) is dlm-suitable.
Definition 3.33. Let
![]() $y \in {}^\omega \omega \cap M_n(x)[g]$
be pre-dlm-suitable as witnessed by some y-premouse
$y \in {}^\omega \omega \cap M_n(x)[g]$
be pre-dlm-suitable as witnessed by some y-premouse
![]() $M(y)$
. We say that y is dlm-suitable (witnessed by
$M(y)$
. We say that y is dlm-suitable (witnessed by
![]() $M(y)$
) iff
$M(y)$
) iff
-
(i) for every
 $s \in [\operatorname {Ord} ]^{<\omega }$
there is a premouse
$s \in [\operatorname {Ord} ]^{<\omega }$
there is a premouse
 $\mathcal {N}$
such that
$\mathcal {N}$
such that
 $(\mathcal {N},s) \in \mathcal {I}^{M(y)}$
and
$(\mathcal {N},s) \in \mathcal {I}^{M(y)}$
and -
(ii) for every
 $\mathcal {N} \in \mathcal {G}^{M(y)}$
,
$\mathcal {N} \in \mathcal {G}^{M(y)}$
,  $$\begin{align*}\mathcal{P}^{M(y)}(\mathcal{N}|\delta^{\mathcal{N}}) = K^{M_n(x)[g]}(\mathcal{N}|\delta^{\mathcal{N}}).\end{align*}$$
$$\begin{align*}\mathcal{P}^{M(y)}(\mathcal{N}|\delta^{\mathcal{N}}) = K^{M_n(x)[g]}(\mathcal{N}|\delta^{\mathcal{N}}).\end{align*}$$
Lemma 3.34.
![]() $M_n(x)$
witnesses that x is dlm-suitable.
$M_n(x)$
witnesses that x is dlm-suitable.
Proof. The fact that
![]() $M_n(x)$
satisfies (i) follows from Lemma 3.13 and Corollary 3.21, so we only have to show (ii). Let
$M_n(x)$
satisfies (i) follows from Lemma 3.13 and Corollary 3.21, so we only have to show (ii). Let
![]() $\mathcal {N} \in \mathcal {G}$
. Then
$\mathcal {N} \in \mathcal {G}$
. Then
 $\mathcal {P}^{M_n(x)}(\mathcal {N}|\delta ^{\mathcal {N}}) = M_n(\mathcal {N}|\delta ^{\mathcal {N}})$
by Lemma 3.20. Moreover, there is some G generic over the result of the
$\mathcal {P}^{M_n(x)}(\mathcal {N}|\delta ^{\mathcal {N}}) = M_n(\mathcal {N}|\delta ^{\mathcal {N}})$
by Lemma 3.20. Moreover, there is some G generic over the result of the
![]() $\mathcal {P}$
-construction
$\mathcal {P}$
-construction
 $\mathcal {P}^{M_n(x)}(\mathcal {N}|\delta ^{\mathcal {N}})$
for the
$\mathcal {P}^{M_n(x)}(\mathcal {N}|\delta ^{\mathcal {N}})$
for the
![]() $\delta ^{\mathcal {N}}$
-generator version of the extender algebra at
$\delta ^{\mathcal {N}}$
-generator version of the extender algebra at
![]() $\delta ^{\mathcal {N}}$
with
$\delta ^{\mathcal {N}}$
with
 $\mathcal {P}^{M_n(x)}(\mathcal {N}|\delta ^{\mathcal {N}})[G] = M_n(x)$
. That means
$\mathcal {P}^{M_n(x)}(\mathcal {N}|\delta ^{\mathcal {N}})[G] = M_n(x)$
. That means
 $$\begin{align*}M_n(\mathcal{N}|\delta^{\mathcal{N}})[G] = M_n(x). \end{align*}$$
$$\begin{align*}M_n(\mathcal{N}|\delta^{\mathcal{N}})[G] = M_n(x). \end{align*}$$
Now,
 $$ \begin{align*} K^{M_n(x)[g]}(\mathcal{N}|\delta^{\mathcal{N}}) & = K^{M_n(\mathcal{N}|\delta^{\mathcal{N}})[G][g]}(\mathcal{N}|\delta^{\mathcal{N}}) = K^{M_n(\mathcal{N}|\delta^{\mathcal{N}})}(\mathcal{N}|\delta^{\mathcal{N}}) \\ & = M_n(\mathcal{N}|\delta^{\mathcal{N}}) = \mathcal{P}^{M_n(x)}(\mathcal{N}|\delta^{\mathcal{N}}), \end{align*} $$
$$ \begin{align*} K^{M_n(x)[g]}(\mathcal{N}|\delta^{\mathcal{N}}) & = K^{M_n(\mathcal{N}|\delta^{\mathcal{N}})[G][g]}(\mathcal{N}|\delta^{\mathcal{N}}) = K^{M_n(\mathcal{N}|\delta^{\mathcal{N}})}(\mathcal{N}|\delta^{\mathcal{N}}) \\ & = M_n(\mathcal{N}|\delta^{\mathcal{N}}) = \mathcal{P}^{M_n(x)}(\mathcal{N}|\delta^{\mathcal{N}}), \end{align*} $$
by generic absoluteness of the core model and Lemma 1.1 in [Reference Schindler14] (due to Steel).⊣
Condition
![]() $(ii)$
in Definition 3.33 will ensure that for any dlm-suitable y-premouse
$(ii)$
in Definition 3.33 will ensure that for any dlm-suitable y-premouse
![]() $M(y)$
and
$M(y)$
and
![]() $(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I} \cap \mathcal {I}^{M(y)}$
with
$(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I} \cap \mathcal {I}^{M(y)}$
with
![]() $(\mathcal {N},s) \leq _{\mathcal {I}} (\mathcal {M},t)$
and
$(\mathcal {N},s) \leq _{\mathcal {I}} (\mathcal {M},t)$
and
![]() $(\mathcal {N},s) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
, the induced embeddings
$(\mathcal {N},s) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
, the induced embeddings
![]() $\pi _{(\mathcal {N},s), (\mathcal {M},t)}$
and
$\pi _{(\mathcal {N},s), (\mathcal {M},t)}$
and
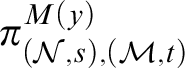 $\pi ^{M(y)}_{(\mathcal {N},s), (\mathcal {M},t)}$
agree. Hence we can show in the following lemma that the direct limit
$\pi ^{M(y)}_{(\mathcal {N},s), (\mathcal {M},t)}$
agree. Hence we can show in the following lemma that the direct limit
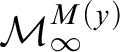 $\mathcal {M}_{\infty }^{M(y)}$
defined inside some dlm-suitable
$\mathcal {M}_{\infty }^{M(y)}$
defined inside some dlm-suitable
![]() $M(y)$
will in fact be the same as the direct limit
$M(y)$
will in fact be the same as the direct limit
![]() $\mathcal {M}_{\infty }$
defined inside
$\mathcal {M}_{\infty }$
defined inside
![]() $M_n(x)$
.
$M_n(x)$
.
Lemma 3.35. Let
![]() $y \in {}^\omega \omega $
be dlm-suitable as witnessed by
$y \in {}^\omega \omega $
be dlm-suitable as witnessed by
![]() $M(y)$
. Then
$M(y)$
. Then
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {F}^{M(y)}$
have cofinally many points in common and
$\mathcal {F}^{M(y)}$
have cofinally many points in common and
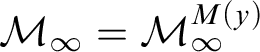 $\mathcal {M}_{\infty } = \mathcal {M}_{\infty }^{M(y)}$
.
$\mathcal {M}_{\infty } = \mathcal {M}_{\infty }^{M(y)}$
.
Proof. Let h be
![]() $\operatorname {Col} (\omega , {<}\kappa )$
-generic over
$\operatorname {Col} (\omega , {<}\kappa )$
-generic over
![]() $M(y)$
such that
$M(y)$
such that
![]() $M(y)[h] = M_n(x)[g]$
. Let
$M(y)[h] = M_n(x)[g]$
. Let
![]() $(\mathcal {N},s) \in \mathcal {I}$
and
$(\mathcal {N},s) \in \mathcal {I}$
and
![]() $(\mathcal {N}^{\prime },s^{\prime }) \in \mathcal {I}^{M(y)}$
. We aim to show that there is some
$(\mathcal {N}^{\prime },s^{\prime }) \in \mathcal {I}^{M(y)}$
. We aim to show that there is some
![]() $(\mathcal {M}, t) \in \mathcal {I} \cap \mathcal {I}^{M(y)}$
such that
$(\mathcal {M}, t) \in \mathcal {I} \cap \mathcal {I}^{M(y)}$
such that
![]() $(\mathcal {N},s) \leq _{\mathcal {I}} (\mathcal {M},t)$
and
$(\mathcal {N},s) \leq _{\mathcal {I}} (\mathcal {M},t)$
and
![]() $(\mathcal {N}^{\prime }, s^{\prime }) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
. As condition (ii) in Definition 3.33 yields that the embeddings associated to
$(\mathcal {N}^{\prime }, s^{\prime }) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
. As condition (ii) in Definition 3.33 yields that the embeddings associated to
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {F}^{M(y)}$
agree, this suffices to show that
$\mathcal {F}^{M(y)}$
agree, this suffices to show that
 $\mathcal {M}_{\infty } = \mathcal {M}_{\infty }^{M(y)}$
.
$\mathcal {M}_{\infty } = \mathcal {M}_{\infty }^{M(y)}$
.
Let
![]() $t = s \cup s^{\prime }$
. By assumption, there is a t-iterable premouse
$t = s \cup s^{\prime }$
. By assumption, there is a t-iterable premouse
![]() $\mathcal {R}$
in
$\mathcal {R}$
in
![]() $M_n(x)$
and a t-iterable premouse
$M_n(x)$
and a t-iterable premouse
![]() $\mathcal {R}^{\prime }$
in
$\mathcal {R}^{\prime }$
in
![]() $M(y)$
. Therefore we can assume that
$M(y)$
. Therefore we can assume that
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {N}^{\prime }$
are both t-iterable in
$\mathcal {N}^{\prime }$
are both t-iterable in
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $M(y)$
respectively as we can replace them by the result of their coiteration with
$M(y)$
respectively as we can replace them by the result of their coiteration with
![]() $\mathcal {R}$
and
$\mathcal {R}$
and
![]() $\mathcal {R}^{\prime }$
respectively.
$\mathcal {R}^{\prime }$
respectively.
By the choice of
![]() $M(y)$
and generic absoluteness of the core model we have
$M(y)$
and generic absoluteness of the core model we have
 $$ \begin{align} M(y) & = (K(y))^{M(y)} = (K(y))^{M(y)[h]} \\ & = (K(y))^{M_n(x)[g]} = (K(y))^{M_n(x)[g \upharpoonright \xi]}, \nonumber \end{align} $$
$$ \begin{align} M(y) & = (K(y))^{M(y)} = (K(y))^{M(y)[h]} \\ & = (K(y))^{M_n(x)[g]} = (K(y))^{M_n(x)[g \upharpoonright \xi]}, \nonumber \end{align} $$
where
![]() $\xi < \kappa $
is such that
$\xi < \kappa $
is such that
![]() $y \in M_n(x)[g \upharpoonright \xi ]$
. Analogously, using Lemma 1.1 in [Reference Schindler14] due to Steel and generic absoluteness of the core model again,
$y \in M_n(x)[g \upharpoonright \xi ]$
. Analogously, using Lemma 1.1 in [Reference Schindler14] due to Steel and generic absoluteness of the core model again,
 $$ \begin{align} M_n(x) & = (K(x))^{M_n(x)} = (K(x))^{M_n(x)[g]} \\ & = (K(x))^{M(y)[h]} = (K(x))^{M(y)[h \upharpoonright \xi^{\prime}]}, \nonumber \end{align} $$
$$ \begin{align} M_n(x) & = (K(x))^{M_n(x)} = (K(x))^{M_n(x)[g]} \\ & = (K(x))^{M(y)[h]} = (K(x))^{M(y)[h \upharpoonright \xi^{\prime}]}, \nonumber \end{align} $$
where
![]() $\xi ^{\prime } < \kappa $
is such that
$\xi ^{\prime } < \kappa $
is such that
![]() $x \in M(y)[h \upharpoonright \xi ^{\prime }]$
. Now we can obtain the following claim.
$x \in M(y)[h \upharpoonright \xi ^{\prime }]$
. Now we can obtain the following claim.
Claim 1.
![]() $M(y)$
and
$M(y)$
and
![]() $M_n(x)$
have cofinally many common cardinal cutpoints below
$M_n(x)$
have cofinally many common cardinal cutpoints below
![]() $\kappa $
.
$\kappa $
.
Proof. As
![]() $M(y) = K(y)^{M_n(x)[g \upharpoonright \xi ]}$
is an inner model of
$M(y) = K(y)^{M_n(x)[g \upharpoonright \xi ]}$
is an inner model of
![]() $M_n(x)[g \upharpoonright \xi ]$
, every cardinal above
$M_n(x)[g \upharpoonright \xi ]$
, every cardinal above
![]() $\xi $
in
$\xi $
in
![]() $M_n(x)$
is a cardinal in
$M_n(x)$
is a cardinal in
![]() $M(y)$
, so it is easy to find cofinally many common cardinals of
$M(y)$
, so it is easy to find cofinally many common cardinals of
![]() $M(y)$
and
$M(y)$
and
![]() $M_n(x)$
below
$M_n(x)$
below
![]() $\kappa $
. Recall that
$\kappa $
. Recall that
![]() $\kappa $
is the least inaccessible cardinal of both
$\kappa $
is the least inaccessible cardinal of both
![]() $M(y)$
and
$M(y)$
and
![]() $M_n(x)$
. Therefore, every common cardinal of
$M_n(x)$
. Therefore, every common cardinal of
![]() $M(y)$
and
$M(y)$
and
![]() $M_n(x)$
below
$M_n(x)$
below
![]() $\kappa $
is also a cutpoint of both models.⊣
$\kappa $
is also a cutpoint of both models.⊣
Moreover, Equations (1) and (2) yield
where
![]() $\xi ^{\prime } < \zeta < \kappa $
is such that
$\xi ^{\prime } < \zeta < \kappa $
is such that
![]() $g \upharpoonright \xi \in M(y)[h \upharpoonright \zeta ]$
. By the intermediate model theorem (see for example Lemma 15.43 in [Reference Jech4]) this implies that
$g \upharpoonright \xi \in M(y)[h \upharpoonright \zeta ]$
. By the intermediate model theorem (see for example Lemma 15.43 in [Reference Jech4]) this implies that
![]() $M_n(x)[g \upharpoonright \xi ]$
is a generic extension of
$M_n(x)[g \upharpoonright \xi ]$
is a generic extension of
![]() $M(y)$
for a forcing of size less than
$M(y)$
for a forcing of size less than
![]() $\kappa $
.Footnote
6
Since
$\kappa $
.Footnote
6
Since
![]() $M_n(x)[g \upharpoonright \xi ]$
is a generic extension of
$M_n(x)[g \upharpoonright \xi ]$
is a generic extension of
![]() $M_n(x)$
for a forcing of size less than
$M_n(x)$
for a forcing of size less than
![]() $\kappa $
as well, this implies by Theorem 1.3 in [Reference Usuba24] that there is some common inner model
$\kappa $
as well, this implies by Theorem 1.3 in [Reference Usuba24] that there is some common inner model
![]() $W \subseteq M_n(x) \cap M(y)$
such that
$W \subseteq M_n(x) \cap M(y)$
such that
![]() $M_n(x)[g \upharpoonright \xi ]$
is a generic extension of W for a forcing of size less than
$M_n(x)[g \upharpoonright \xi ]$
is a generic extension of W for a forcing of size less than
![]() $\kappa $
.
$\kappa $
.
As every generic extension via a forcing of size less than
![]() $\kappa $
can be absorbed by the collapse of some ordinal
$\kappa $
can be absorbed by the collapse of some ordinal
![]() $\beta < \kappa $
, this yields that we can fix some ordinal
$\beta < \kappa $
, this yields that we can fix some ordinal
![]() $\beta < \kappa $
and some
$\beta < \kappa $
and some
![]() $\operatorname {Col} (\omega ,\beta )$
-generic
$\operatorname {Col} (\omega ,\beta )$
-generic
![]() $b \in M_n(x)[g]$
over W such that
$b \in M_n(x)[g]$
over W such that
![]() $x,y,\mathcal {N},\mathcal {N}^{\prime } \in W[b]$
. Then
$x,y,\mathcal {N},\mathcal {N}^{\prime } \in W[b]$
. Then
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $M(y)$
exist in
$M(y)$
exist in
![]() $W[b]$
as definable subclasses because
$W[b]$
as definable subclasses because
 $$\begin{align*}(K(x))^{W[b]} = (K(x))^{M_n(x)[g \upharpoonright \xi]} = (K(x))^{M_n(x)} = M_n(x)\end{align*}$$
$$\begin{align*}(K(x))^{W[b]} = (K(x))^{M_n(x)[g \upharpoonright \xi]} = (K(x))^{M_n(x)} = M_n(x)\end{align*}$$
and similarly
 $$\begin{align*}(K(y))^{W[b]} = (K(y))^{M_n(x)[g \upharpoonright \xi]} = (K(y))^{M_n(x)[g]} = (K(y))^{M(y)[h]}= M(y)\end{align*}$$
$$\begin{align*}(K(y))^{W[b]} = (K(y))^{M_n(x)[g \upharpoonright \xi]} = (K(y))^{M_n(x)[g]} = (K(y))^{M(y)[h]}= M(y)\end{align*}$$
by generic absoluteness of the core model again. Let
![]() $\dot {x},\dot {y},\dot {\mathcal {N}}$
and
$\dot {x},\dot {y},\dot {\mathcal {N}}$
and
![]() $\dot {\mathcal {N}^{\prime }}$
be
$\dot {\mathcal {N}^{\prime }}$
be
![]() $\operatorname {Col} (\omega ,\beta )$
-names for
$\operatorname {Col} (\omega ,\beta )$
-names for
![]() $x,y,\mathcal {N}$
and
$x,y,\mathcal {N}$
and
![]() $\mathcal {N}^{\prime }$
in W. Moreover, let
$\mathcal {N}^{\prime }$
in W. Moreover, let
![]() $p \in \operatorname {Col} (\omega ,\beta )$
force all properties we need about
$p \in \operatorname {Col} (\omega ,\beta )$
force all properties we need about
![]() $\dot {x},\dot {y},\dot {\mathcal {N}}$
and
$\dot {x},\dot {y},\dot {\mathcal {N}}$
and
![]() $\dot {\mathcal {N}^{\prime }}$
. For
$\dot {\mathcal {N}^{\prime }}$
. For
![]() $q \leq _{\operatorname {Col} (\omega ,\beta )} p$
let
$q \leq _{\operatorname {Col} (\omega ,\beta )} p$
let
![]() $b_q$
be the
$b_q$
be the
![]() $\operatorname {Col} (\omega ,\beta )$
-generic filter over W such that
$\operatorname {Col} (\omega ,\beta )$
-generic filter over W such that
![]() $\bigcup b_q$
agrees with q on
$\bigcup b_q$
agrees with q on
![]() $\operatorname {dom}(q)$
and with
$\operatorname {dom}(q)$
and with
![]() $\bigcup b$
everywhere else.
$\bigcup b$
everywhere else.
Now we construct
![]() $(\mathcal {M}, t) \in \mathcal {I} \cap \mathcal {I}^{M(y)}$
. Let
$(\mathcal {M}, t) \in \mathcal {I} \cap \mathcal {I}^{M(y)}$
. Let
![]() $\eta < \kappa $
be a cardinal cutpoint of both
$\eta < \kappa $
be a cardinal cutpoint of both
![]() $M(y)$
and
$M(y)$
and
![]() $M_n(x)$
such that
$M_n(x)$
such that
![]() $\xi , \xi ^{\prime } < \eta $
, which exists by Claim 1. Then in fact
$\xi , \xi ^{\prime } < \eta $
, which exists by Claim 1. Then in fact
![]() $(\eta ^+)^{M_n(x)} = (\eta ^+)^{M(y)}$
as by Equations (1) and (2) at the beginning of the proof
$(\eta ^+)^{M_n(x)} = (\eta ^+)^{M(y)}$
as by Equations (1) and (2) at the beginning of the proof
 $$\begin{align*}(\eta^+)^{M(y)} \leq (\eta^+)^{M_n(x)[g \upharpoonright \xi]} = (\eta^+)^{M_n(x)} \leq (\eta^+)^{M(y)[h \upharpoonright \xi^{\prime}]} = (\eta^+)^{M(y)}. \end{align*}$$
$$\begin{align*}(\eta^+)^{M(y)} \leq (\eta^+)^{M_n(x)[g \upharpoonright \xi]} = (\eta^+)^{M_n(x)} \leq (\eta^+)^{M(y)[h \upharpoonright \xi^{\prime}]} = (\eta^+)^{M(y)}. \end{align*}$$
By the same argument,
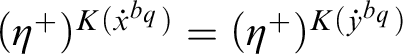 $(\eta ^+)^{K(\dot {x}^{b_q})} = (\eta ^+)^{K(\dot {y}^{b_q})}$
for all
$(\eta ^+)^{K(\dot {x}^{b_q})} = (\eta ^+)^{K(\dot {y}^{b_q})}$
for all
![]() $q \leq _{\operatorname {Col} (\omega ,\beta )} p$
.
$q \leq _{\operatorname {Col} (\omega ,\beta )} p$
.
Work in
![]() $W[b]$
. Using Lemmas 3.8 and 3.9, we obtain an inner model
$W[b]$
. Using Lemmas 3.8 and 3.9, we obtain an inner model
![]() $\mathcal {M}$
by pseudo-comparing all
$\mathcal {M}$
by pseudo-comparing all
![]() $(\dot {\mathcal {N}})^{b_q}$
and
$(\dot {\mathcal {N}})^{b_q}$
and
![]() $(\dot {\mathcal {N}^{\prime }})^{b_q}$
for
$(\dot {\mathcal {N}^{\prime }})^{b_q}$
for
![]() $q \leq _{\operatorname {Col} (\omega ,\beta )} p$
and simultaneously pseudo-genericity iterating such that
$q \leq _{\operatorname {Col} (\omega ,\beta )} p$
and simultaneously pseudo-genericity iterating such that
![]() $K(\dot {x}^{b_q}) | \eta $
and
$K(\dot {x}^{b_q}) | \eta $
and
![]() $K(\dot {y}^{b_q}) | \eta $
are generic over
$K(\dot {y}^{b_q}) | \eta $
are generic over
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
 $\delta ^{\mathcal {M}} = (\eta ^+)^{K(\dot {x}^{b_q})} = (\eta ^+)^{K(\dot {y}^{b_q})}$
. Since
$\delta ^{\mathcal {M}} = (\eta ^+)^{K(\dot {x}^{b_q})} = (\eta ^+)^{K(\dot {y}^{b_q})}$
. Since
![]() $\mathcal {M}$
is definable in
$\mathcal {M}$
is definable in
![]() $W[b]$
from
$W[b]$
from
![]() $\{b_q \mid q \leq _{\operatorname {Col} (\omega ,\beta )} p \}$
and parameters from W, we have that in fact
$\{b_q \mid q \leq _{\operatorname {Col} (\omega ,\beta )} p \}$
and parameters from W, we have that in fact
![]() $\mathcal {M} \in W \subseteq M_n(x) \cap M(y)$
, as
$\mathcal {M} \in W \subseteq M_n(x) \cap M(y)$
, as
![]() $\mathcal {M}$
does not depend on the choice of the generic b. Moreover,
$\mathcal {M}$
does not depend on the choice of the generic b. Moreover,
![]() $\mathcal {M}$
is a correct iterate of
$\mathcal {M}$
is a correct iterate of
![]() $\mathcal {N}$
in
$\mathcal {N}$
in
![]() $M_n(x)$
and a correct iterate of
$M_n(x)$
and a correct iterate of
![]() $\mathcal {N}^{\prime }$
in
$\mathcal {N}^{\prime }$
in
![]() $M(y)$
.
$M(y)$
.
As argued above, we can assume that
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {N}^{\prime }$
are t-iterable in
$\mathcal {N}^{\prime }$
are t-iterable in
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $M(y)$
respectively for
$M(y)$
respectively for
![]() $t = s \cup s^{\prime }$
. Therefore
$t = s \cup s^{\prime }$
. Therefore
![]() $\mathcal {M}$
is t-iterable in both,
$\mathcal {M}$
is t-iterable in both,
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $M(y)$
. Hence,
$M(y)$
. Hence,
![]() $(\mathcal {M},t) \kern1.2pt{\in}\kern1.2pt \mathcal {I} \kern1.2pt{\cap}\kern1.2pt \mathcal {I}^{M(y)}$
,
$(\mathcal {M},t) \kern1.2pt{\in}\kern1.2pt \mathcal {I} \kern1.2pt{\cap}\kern1.2pt \mathcal {I}^{M(y)}$
,
![]() $(\mathcal {N},s) \kern1.2pt{\leq _{\mathcal {I}}}\kern1.2pt (\mathcal {M},t)$
, and
$(\mathcal {N},s) \kern1.2pt{\leq _{\mathcal {I}}}\kern1.2pt (\mathcal {M},t)$
, and
![]() $(\mathcal {N}^{\prime }, s^{\prime }) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
, as desired.⊣
$(\mathcal {N}^{\prime }, s^{\prime }) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
, as desired.⊣
This yields that
 $\mathcal {M}_{\infty } \in \operatorname {HOD}^{M_n(x)[g]} $
.
$\mathcal {M}_{\infty } \in \operatorname {HOD}^{M_n(x)[g]} $
.
4
 $\operatorname {HOD} $
below
$\operatorname {HOD} $
below
 $\delta_{\infty }$
$\delta_{\infty }$
In this section we will show that
![]() $\operatorname {HOD}^{M_n(x)[g]} $
and
$\operatorname {HOD}^{M_n(x)[g]} $
and
![]() $\mathcal {M}_{\infty }$
agree up to
$\mathcal {M}_{\infty }$
agree up to
![]() $\delta _{\infty }$
by generalizing the arguments in Section 3.4 in [Reference Steel, Woodin, Kechris, Löwe and Steel23]. We show a version of Woodin’s derived model resemblance for our setting. For this, we do not need to talk about generic extensions such as
$\delta _{\infty }$
by generalizing the arguments in Section 3.4 in [Reference Steel, Woodin, Kechris, Löwe and Steel23]. We show a version of Woodin’s derived model resemblance for our setting. For this, we do not need to talk about generic extensions such as
![]() $M(y)[h]$
and work with
$M(y)[h]$
and work with
![]() $M(y)$
directly instead.
$M(y)$
directly instead.
We start with expanding our direct limit
![]() $\mathcal {M}_{\infty }$
to the proper class premouse
$\mathcal {M}_{\infty }$
to the proper class premouse
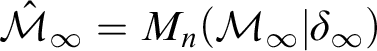 $\hat {\mathcal {M}}_{\infty } = M_n(\mathcal {M}_{\infty } | \delta _{\infty })$
and define a direct limit system
$\hat {\mathcal {M}}_{\infty } = M_n(\mathcal {M}_{\infty } | \delta _{\infty })$
and define a direct limit system
![]() $\hat {\mathcal {F}}$
of expansions of the elements of
$\hat {\mathcal {F}}$
of expansions of the elements of
![]() $\mathcal {F}$
that converges to
$\mathcal {F}$
that converges to
![]() $\hat {\mathcal {M}}_{\infty }$
. For an n-suitable premouse
$\hat {\mathcal {M}}_{\infty }$
. For an n-suitable premouse
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
with
$s \in [\operatorname {Ord} ]^{<\omega }$
with
![]() $max(s)$
a uniform indiscernible above the Woodin cardinals in
$max(s)$
a uniform indiscernible above the Woodin cardinals in
![]() $M_n(\mathcal {N}|\delta ^{\mathcal {N}})$
, we let
$M_n(\mathcal {N}|\delta ^{\mathcal {N}})$
, we let
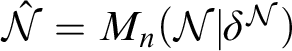 $\hat {\mathcal {N}} = M_n(\mathcal {N} | \delta ^{\mathcal {N}})$
be the proper class expansion of
$\hat {\mathcal {N}} = M_n(\mathcal {N} | \delta ^{\mathcal {N}})$
be the proper class expansion of
![]() $\mathcal {N}$
,
$\mathcal {N}$
,
![]() $s^- = s \setminus max(s)$
,
$s^- = s \setminus max(s)$
,
 $$\begin{align*}\gamma_s^{\hat{\mathcal{N}}} = \sup(Hull_1^{\hat{\mathcal{N}} | max(s)}(s^-) \cap \delta^{\mathcal{N}}), \end{align*}$$
$$\begin{align*}\gamma_s^{\hat{\mathcal{N}}} = \sup(Hull_1^{\hat{\mathcal{N}} | max(s)}(s^-) \cap \delta^{\mathcal{N}}), \end{align*}$$
and
 $$\begin{align*}H_s^{\hat{\mathcal{N}}} = Hull_1^{\hat{\mathcal{N}} | max(s)}(\gamma_s^{\hat{\mathcal{N}}} \cup s^-). \end{align*}$$
$$\begin{align*}H_s^{\hat{\mathcal{N}}} = Hull_1^{\hat{\mathcal{N}} | max(s)}(\gamma_s^{\hat{\mathcal{N}}} \cup s^-). \end{align*}$$
Now we let
 $$\begin{align*}\hat{\mathcal{F}} = \{ H_s^{\hat{\mathcal{N}}} \mid (\mathcal{N},s) \in \mathcal{I} \} \end{align*}$$
$$\begin{align*}\hat{\mathcal{F}} = \{ H_s^{\hat{\mathcal{N}}} \mid (\mathcal{N},s) \in \mathcal{I} \} \end{align*}$$
and for
![]() $(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}$
with
$(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}$
with
![]() $(\mathcal {N},s) \leq (\mathcal {M},t)$
we let
$(\mathcal {N},s) \leq (\mathcal {M},t)$
we let
 $\hat {\pi }_{(\mathcal {N},s),(\mathcal {M},t)} : H_s^{\hat {\mathcal {N}}} \rightarrow H_t^{\hat {\mathcal {M}}}$
denote the canonical corresponding embedding extending
$\hat {\pi }_{(\mathcal {N},s),(\mathcal {M},t)} : H_s^{\hat {\mathcal {N}}} \rightarrow H_t^{\hat {\mathcal {M}}}$
denote the canonical corresponding embedding extending
![]() $\pi _{(\mathcal {N},s^-),(\mathcal {M},t^-)}$
.
$\pi _{(\mathcal {N},s^-),(\mathcal {M},t^-)}$
.
Finally, let
![]() $\hat {\mathcal {M}}_{\infty }$
be the direct limit of
$\hat {\mathcal {M}}_{\infty }$
be the direct limit of
![]() $(\hat {\mathcal {F}}, \leq )$
under the embeddings
$(\hat {\mathcal {F}}, \leq )$
under the embeddings
![]() $\hat {\pi }_{(\mathcal {N},s),(\mathcal {M},t)}$
and let
$\hat {\pi }_{(\mathcal {N},s),(\mathcal {M},t)}$
and let
 $\hat {\pi }_{(\mathcal {N},s),\infty } : H_s^{\hat {\mathcal {N}}} \rightarrow \hat {\mathcal {M}}_{\infty }$
for
$\hat {\pi }_{(\mathcal {N},s),\infty } : H_s^{\hat {\mathcal {N}}} \rightarrow \hat {\mathcal {M}}_{\infty }$
for
![]() $(\mathcal {N},s) \in \mathcal {I}$
denote the direct limit embedding. Then it is easy to see that
$(\mathcal {N},s) \in \mathcal {I}$
denote the direct limit embedding. Then it is easy to see that
 $M_n(\mathcal {M}_{\infty } | \delta _{\infty }) = \hat {\mathcal {M}}_{\infty }$
as we can define a similar direct limit system
$M_n(\mathcal {M}_{\infty } | \delta _{\infty }) = \hat {\mathcal {M}}_{\infty }$
as we can define a similar direct limit system
![]() $\hat {\mathcal {F}}^+$
of premice expanding the n-suitable premice in
$\hat {\mathcal {F}}^+$
of premice expanding the n-suitable premice in
![]() $\mathcal {F}^+$
.
$\mathcal {F}^+$
.
Choose for any ordinal
![]() $\alpha $
an arbitrary
$\alpha $
an arbitrary
![]() $(\mathcal {N},s) \in \mathcal {I}$
such that
$(\mathcal {N},s) \in \mathcal {I}$
such that
![]() $\alpha \in s \setminus max(s)$
and let
$\alpha \in s \setminus max(s)$
and let
![]() $\alpha ^* = \hat {\pi }_{(\mathcal {N},s),\infty }(\alpha )$
. Note that the value of
$\alpha ^* = \hat {\pi }_{(\mathcal {N},s),\infty }(\alpha )$
. Note that the value of
![]() $\alpha ^*$
does not depend on the choice of
$\alpha ^*$
does not depend on the choice of
![]() $(\mathcal {N},s)$
. We also let
$(\mathcal {N},s)$
. We also let
![]() $t^* = \{ \alpha ^* \mid \alpha \in t \}$
for
$t^* = \{ \alpha ^* \mid \alpha \in t \}$
for
![]() $t \in [\operatorname {Ord} ]^{<\omega }$
.
$t \in [\operatorname {Ord} ]^{<\omega }$
.
Lemma 4.1. Let
![]() $\mathcal {N}$
be an n-suitable premouse and
$\mathcal {N}$
be an n-suitable premouse and
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
such that
$s \in [\operatorname {Ord} ]^{<\omega }$
such that
![]() $(\mathcal {N}, s) \in \mathcal {I}$
. Let
$(\mathcal {N}, s) \in \mathcal {I}$
. Let
 $\bar {\xi } < \gamma _s^{\mathcal {N}}$
,
$\bar {\xi } < \gamma _s^{\mathcal {N}}$
,
 $\xi = \pi _{(\mathcal {N},s),\infty }(\bar {\xi })$
and
$\xi = \pi _{(\mathcal {N},s),\infty }(\bar {\xi })$
and
![]() $t \in [\operatorname {Ord} ]^{<\omega }$
. Moreover, let
$t \in [\operatorname {Ord} ]^{<\omega }$
. Moreover, let
![]() $\varphi (v_0,v_1)$
be a formula in the language of premice, i.e., we allow the extender sequence as a predicate. Then the following are equivalent.
$\varphi (v_0,v_1)$
be a formula in the language of premice, i.e., we allow the extender sequence as a predicate. Then the following are equivalent.
-
(a)
 $M_n(\mathcal {M}_{\infty } | \delta _{\infty }) \vDash \varphi (\xi , t^*)$
and
$M_n(\mathcal {M}_{\infty } | \delta _{\infty }) \vDash \varphi (\xi , t^*)$
and -
(b) in
 $M_n(x)[g]$
, there is some dlm-suitable
$M_n(x)[g]$
, there is some dlm-suitable
 $y \in {}^\omega \omega $
witnessed by
$y \in {}^\omega \omega $
witnessed by
 $M(y)$
with
$M(y)$
with
 $(\mathcal {N},s) \in \mathcal {I}^{M(y)}$
and a correctly guided finite stack on
$(\mathcal {N},s) \in \mathcal {I}^{M(y)}$
and a correctly guided finite stack on
 $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
 $\mathcal {M} \in M(y)$
such that whenever
$\mathcal {M} \in M(y)$
such that whenever
 $\mathcal {R} \in \mathcal {G}^{M(y)}$
is the last model of a correctly guided finite stack on
$\mathcal {R} \in \mathcal {G}^{M(y)}$
is the last model of a correctly guided finite stack on
 $\mathcal {M}$
, then
$\mathcal {M}$
, then
 $\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \varphi (\pi ^{M(y)}_{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi }), t)$
.
$\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \varphi (\pi ^{M(y)}_{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi }), t)$
.
Proof. To prove that
![]() $(a)$
implies
$(a)$
implies
![]() $(b)$
we assume toward a contradiction that
$(b)$
we assume toward a contradiction that
![]() $(b)$
is false. So in
$(b)$
is false. So in
![]() $M_n(x)[g]$
for all dlm-suitable
$M_n(x)[g]$
for all dlm-suitable
![]() $y \in {}^\omega \omega $
and
$y \in {}^\omega \omega $
and
![]() $M(y)$
witnessing this with
$M(y)$
witnessing this with
![]() $(\mathcal {N}, s) \in \mathcal {I}^{M(y)}$
and all correctly guided finite stacks on
$(\mathcal {N}, s) \in \mathcal {I}^{M(y)}$
and all correctly guided finite stacks on
![]() $\mathcal {N}$
with last model
$\mathcal {N}$
with last model
![]() $\mathcal {M} \in M(y)$
, there is a correctly guided finite stack on
$\mathcal {M} \in M(y)$
, there is a correctly guided finite stack on
![]() $\mathcal {M}$
with last model
$\mathcal {M}$
with last model
![]() $\mathcal {R} \in \mathcal {G}^{M(y)}$
such that
$\mathcal {R} \in \mathcal {G}^{M(y)}$
such that
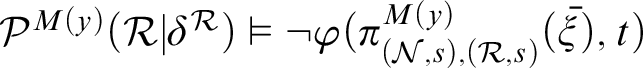 $\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \neg \varphi (\pi ^{M(y)}_{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi }), t)$
.
$\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \neg \varphi (\pi ^{M(y)}_{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi }), t)$
.
We can assume without loss of generality that
![]() $\mathcal {N} \in M_n(x)$
is the last model of a correctly guided finite stack on
$\mathcal {N} \in M_n(x)$
is the last model of a correctly guided finite stack on
![]() $M_{n+1}^-$
via the canonical iteration strategy
$M_{n+1}^-$
via the canonical iteration strategy
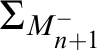 $\Sigma _{M_{n+1}^-}$
and strongly s-iterable below
$\Sigma _{M_{n+1}^-}$
and strongly s-iterable below
![]() $\kappa $
. Moreover, we can assume that
$\kappa $
. Moreover, we can assume that
![]() $max(s)$
is a uniform indiscernible. If this is not already the case, we replace
$max(s)$
is a uniform indiscernible. If this is not already the case, we replace
![]() $\mathcal {N}$
by a pseudo-iterate of the result of the pseudo-comparison of
$\mathcal {N}$
by a pseudo-iterate of the result of the pseudo-comparison of
![]() $\mathcal {N}$
with
$\mathcal {N}$
with
![]() $M_{n+1}^-$
using Lemma 3.8 and Corollary 3.21.
$M_{n+1}^-$
using Lemma 3.8 and Corollary 3.21.
Claim 1. There are n-suitable premice
![]() $\mathcal {N}_k \in \mathcal {F}^+$
for
$\mathcal {N}_k \in \mathcal {F}^+$
for
![]() $k < \omega $
which are cofinal in
$k < \omega $
which are cofinal in
![]() $\mathcal {F}^+$
such that
$\mathcal {F}^+$
such that
![]() $\mathcal {N}_0 = \mathcal {N}$
and for all
$\mathcal {N}_0 = \mathcal {N}$
and for all
![]() $k<\omega $
,
$k<\omega $
,
 $$\begin{align*}M_n(\mathcal{N}_k|\delta^{\mathcal{N}_k}) \vDash \neg\varphi(\bar{\xi}_k,t), \end{align*}$$
$$\begin{align*}M_n(\mathcal{N}_k|\delta^{\mathcal{N}_k}) \vDash \neg\varphi(\bar{\xi}_k,t), \end{align*}$$
where
 $\bar {\xi }_k = i_{\mathcal {N}_0,\mathcal {N}_k}(\bar {\xi })$
is the image of
$\bar {\xi }_k = i_{\mathcal {N}_0,\mathcal {N}_k}(\bar {\xi })$
is the image of
![]() $\bar {\xi }$
under the iteration map induced by
$\bar {\xi }$
under the iteration map induced by
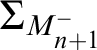 $\Sigma _{M_{n+1}^-}$
.
$\Sigma _{M_{n+1}^-}$
.
Proof. Let
![]() $(\mathcal {Q}_i \mid i < \omega )$
be an enumeration of
$(\mathcal {Q}_i \mid i < \omega )$
be an enumeration of
![]() $\mathcal {F}^+$
and
$\mathcal {F}^+$
and
![]() $\mathcal {N}_0 = \mathcal {N}$
. Then we construct
$\mathcal {N}_0 = \mathcal {N}$
. Then we construct
![]() $\mathcal {N}_{k+1}$
inductively. So assume that we already constructed
$\mathcal {N}_{k+1}$
inductively. So assume that we already constructed
![]() $\mathcal {N}_k$
and pseudo-coiterate
$\mathcal {N}_k$
and pseudo-coiterate
![]() $\mathcal {N}_k$
with
$\mathcal {N}_k$
with
![]() $\mathcal {Q}_k$
to some model
$\mathcal {Q}_k$
to some model
![]() $\mathcal {N}_k^*$
(see Lemma 3.8). By assumption
$\mathcal {N}_k^*$
(see Lemma 3.8). By assumption
![]() $(b)$
is false, so let
$(b)$
is false, so let
![]() $\mathcal {R}$
be a counterexample witnessing this for
$\mathcal {R}$
be a counterexample witnessing this for
![]() $\mathcal {N}_k^*$
and the dlm-suitable premouse
$\mathcal {N}_k^*$
and the dlm-suitable premouse
![]() $M_n(x)$
. That means
$M_n(x)$
. That means
![]() $\mathcal {R} \in \mathcal {G}$
is the last model of a correctly guided finite stack on
$\mathcal {R} \in \mathcal {G}$
is the last model of a correctly guided finite stack on
![]() $\mathcal {N}_k^*$
such that
$\mathcal {N}_k^*$
such that
 $M_n(\mathcal {R}|\delta ^{\mathcal {R}}) = \mathcal {P}^{M_n(x)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \neg \varphi (i_{\mathcal {N},\mathcal {R}}(\bar {\xi }),t)$
as
$M_n(\mathcal {R}|\delta ^{\mathcal {R}}) = \mathcal {P}^{M_n(x)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \neg \varphi (i_{\mathcal {N},\mathcal {R}}(\bar {\xi }),t)$
as
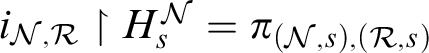 $i_{\mathcal {N},\mathcal {R}} \upharpoonright H_s^{\mathcal {N}} = \pi _{(\mathcal {N},s),(\mathcal {R},s)}$
. But
$i_{\mathcal {N},\mathcal {R}} \upharpoonright H_s^{\mathcal {N}} = \pi _{(\mathcal {N},s),(\mathcal {R},s)}$
. But
![]() $\mathcal {R} \in \mathcal {F}^+$
since
$\mathcal {R} \in \mathcal {F}^+$
since
![]() $\mathcal {R} \in \mathcal {G}$
and it is a correct iterate of
$\mathcal {R} \in \mathcal {G}$
and it is a correct iterate of
![]() $\mathcal {Q}_k$
. Thus we can let
$\mathcal {Q}_k$
. Thus we can let
![]() $\mathcal {N}_{k+1} = \mathcal {R}$
.⊣
$\mathcal {N}_{k+1} = \mathcal {R}$
.⊣
Since
![]() $(\mathcal {N}_k \mid k < \omega )$
is cofinal in
$(\mathcal {N}_k \mid k < \omega )$
is cofinal in
![]() $\mathcal {F}^+$
, it follows that the direct limit of
$\mathcal {F}^+$
, it follows that the direct limit of
![]() $(\mathcal {N}_k, i_{\mathcal {N}_k,\mathcal {N}_l} \mid k<l<\omega )$
is equal to
$(\mathcal {N}_k, i_{\mathcal {N}_k,\mathcal {N}_l} \mid k<l<\omega )$
is equal to
![]() $\mathcal {M}_{\infty }^+$
. Let
$\mathcal {M}_{\infty }^+$
. Let
 $\hat {\mathcal {N}_k} = M_n(\mathcal {N}_k | \delta ^{\mathcal {N}_k})$
and let
$\hat {\mathcal {N}_k} = M_n(\mathcal {N}_k | \delta ^{\mathcal {N}_k})$
and let
 $\hat {i}_{\hat {\mathcal {N}}_k,\infty } : \hat {\mathcal {N}_k} \rightarrow M_n(\mathcal {M}_{\infty }^+ | \delta ^{\mathcal {M}_{\infty }^+}) = \hat {\mathcal {M}}_{\infty }^+$
be the corresponding extension of the direct limit map
$\hat {i}_{\hat {\mathcal {N}}_k,\infty } : \hat {\mathcal {N}_k} \rightarrow M_n(\mathcal {M}_{\infty }^+ | \delta ^{\mathcal {M}_{\infty }^+}) = \hat {\mathcal {M}}_{\infty }^+$
be the corresponding extension of the direct limit map
![]() $i_{\mathcal {N}_k, \infty }$
. Then we have for all sufficiently large k that
$i_{\mathcal {N}_k, \infty }$
. Then we have for all sufficiently large k that
 $$\begin{align*}M_n(\mathcal{M}_{\infty}^+ | \delta^{\mathcal{M}_{\infty}^+}) \vDash \neg\varphi(i_{\mathcal{N}_k, \infty}(\bar{\xi}_k), \hat{i}_{\hat{\mathcal{N}}_k,\infty}[t]). \end{align*}$$
$$\begin{align*}M_n(\mathcal{M}_{\infty}^+ | \delta^{\mathcal{M}_{\infty}^+}) \vDash \neg\varphi(i_{\mathcal{N}_k, \infty}(\bar{\xi}_k), \hat{i}_{\hat{\mathcal{N}}_k,\infty}[t]). \end{align*}$$
Since we assumed that
![]() $\mathcal {N}$
is strongly s-iterable below
$\mathcal {N}$
is strongly s-iterable below
![]() $\kappa $
and
$\kappa $
and
 $\bar {\xi } < \gamma _s^{\mathcal {N}}$
, it follows that
$\bar {\xi } < \gamma _s^{\mathcal {N}}$
, it follows that
 $i_{\mathcal {N}_k, \infty }(\bar {\xi }_k) = i_{\mathcal {N},\infty }(\bar {\xi }) = \pi _{(\mathcal {N},s),\infty }(\bar {\xi }) = \xi $
as
$i_{\mathcal {N}_k, \infty }(\bar {\xi }_k) = i_{\mathcal {N},\infty }(\bar {\xi }) = \pi _{(\mathcal {N},s),\infty }(\bar {\xi }) = \xi $
as
 $\bar {\xi }_k = i_{\mathcal {N},\mathcal {N}_k}(\bar {\xi })$
.
$\bar {\xi }_k = i_{\mathcal {N},\mathcal {N}_k}(\bar {\xi })$
.
Let
![]() $k<\omega $
be large enough such that
$k<\omega $
be large enough such that
![]() $(\mathcal {N}_k, s \cup t) \in \mathcal {I}$
and
$(\mathcal {N}_k, s \cup t) \in \mathcal {I}$
and
 $\hat {i}_{\hat {\mathcal {N}}_l,\hat {\mathcal {N}}_{l+1}}(s \cup t) = s \cup t$
for all
$\hat {i}_{\hat {\mathcal {N}}_l,\hat {\mathcal {N}}_{l+1}}(s \cup t) = s \cup t$
for all
![]() $l \geq k$
. Such a k exists by a so-called bad sequence argument similar to the one in the proof of Lemma 5.8 in [Reference Sargsyan12].
$l \geq k$
. Such a k exists by a so-called bad sequence argument similar to the one in the proof of Lemma 5.8 in [Reference Sargsyan12].
Consider the map
 $$\begin{align*}\hat{\sigma}: M_n(\mathcal{M}_{\infty}|\delta_{\infty}) = \hat{\mathcal{M}}_{\infty} \rightarrow \hat{\mathcal{M}}_{\infty}^+ = M_n(\mathcal{M}_{\infty}^+|\delta^{\mathcal{M}_{\infty}^+}) \end{align*}$$
$$\begin{align*}\hat{\sigma}: M_n(\mathcal{M}_{\infty}|\delta_{\infty}) = \hat{\mathcal{M}}_{\infty} \rightarrow \hat{\mathcal{M}}_{\infty}^+ = M_n(\mathcal{M}_{\infty}^+|\delta^{\mathcal{M}_{\infty}^+}) \end{align*}$$
which is the canonical extension of the map
![]() $\sigma : \mathcal {M}_{\infty } \rightarrow \mathcal {M}_{\infty }^+$
defined in the proof of Lemma 3.28. That means, for
$\sigma : \mathcal {M}_{\infty } \rightarrow \mathcal {M}_{\infty }^+$
defined in the proof of Lemma 3.28. That means, for
![]() $x \in \hat {\mathcal {M}}_{\infty }$
, say
$x \in \hat {\mathcal {M}}_{\infty }$
, say
 $x = \hat {\pi }_{(\mathcal {N}_l,r),\infty }(\bar {x})$
for some
$x = \hat {\pi }_{(\mathcal {N}_l,r),\infty }(\bar {x})$
for some
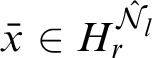 $\bar {x} \in H_r^{\hat {\mathcal {N}}_l}$
, we may assume similar as above that
$\bar {x} \in H_r^{\hat {\mathcal {N}}_l}$
, we may assume similar as above that
![]() $l \geq k$
is large enough such that
$l \geq k$
is large enough such that
![]() $(\mathcal {N}_l,r) \in \mathcal {I}$
and
$(\mathcal {N}_l,r) \in \mathcal {I}$
and
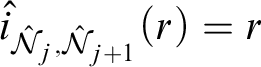 $\hat {i}_{\hat {\mathcal {N}}_j,\hat {\mathcal {N}}_{j+1}}(r) = r$
for all
$\hat {i}_{\hat {\mathcal {N}}_j,\hat {\mathcal {N}}_{j+1}}(r) = r$
for all
![]() $j \geq l$
. Then we let
$j \geq l$
. Then we let
 $\hat {\sigma }(x) = \hat {i}_{\hat {\mathcal {N}}_l,\infty }(\bar {x})$
. Now it follows from a generalization of the proof of [Reference Schlutzenberg16, Claim 2] that
$\hat {\sigma }(x) = \hat {i}_{\hat {\mathcal {N}}_l,\infty }(\bar {x})$
. Now it follows from a generalization of the proof of [Reference Schlutzenberg16, Claim 2] that
![]() $\hat {\sigma } = \operatorname {id}$
. Moreover, we have that
$\hat {\sigma } = \operatorname {id}$
. Moreover, we have that
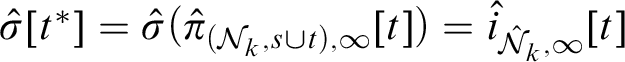 $\hat {\sigma }[t^*] = \hat {\sigma }(\hat {\pi }_{(\mathcal {N}_k,s \cup t),\infty }[t]) = \hat {i}_{\hat {\mathcal {N}}_k,\infty }[t]$
. Therefore pulling back under
$\hat {\sigma }[t^*] = \hat {\sigma }(\hat {\pi }_{(\mathcal {N}_k,s \cup t),\infty }[t]) = \hat {i}_{\hat {\mathcal {N}}_k,\infty }[t]$
. Therefore pulling back under
![]() $\hat {\sigma }$
yields that
$\hat {\sigma }$
yields that
This is the desired contradiction to
![]() $(a)$
.
$(a)$
.
To show that
![]() $(b)$
implies
$(b)$
implies
![]() $(a)$
we now assume that
$(a)$
we now assume that
![]() $(b)$
is true. Let
$(b)$
is true. Let
![]() $M(y)$
be the dlm-suitable premouse with
$M(y)$
be the dlm-suitable premouse with
![]() $(\mathcal {N},s) \in \mathcal {I}^{M(y)}$
given by
$(\mathcal {N},s) \in \mathcal {I}^{M(y)}$
given by
![]() $(b)$
. As before we can assume without loss of generality that
$(b)$
. As before we can assume without loss of generality that
![]() $\mathcal {N}$
is the last model of a correctly guided finite stack on
$\mathcal {N}$
is the last model of a correctly guided finite stack on
![]() $M_{n+1}^-$
via the canonical iteration strategy
$M_{n+1}^-$
via the canonical iteration strategy
 $\Sigma _{M_{n+1}^-}$
, that
$\Sigma _{M_{n+1}^-}$
, that
![]() $\mathcal {N}$
is strongly s-iterable below
$\mathcal {N}$
is strongly s-iterable below
![]() $\kappa $
with respect to branches chosen by
$\kappa $
with respect to branches chosen by
 $\Sigma _{M_{n+1}^-}$
, that
$\Sigma _{M_{n+1}^-}$
, that
![]() $max(s)$
is a uniform indiscernible, and that
$max(s)$
is a uniform indiscernible, and that
![]() $\mathcal {N} \in \mathcal {G} \cap \mathcal {G}^{M(y)}$
using Lemma 3.35.
$\mathcal {N} \in \mathcal {G} \cap \mathcal {G}^{M(y)}$
using Lemma 3.35.
Claim 2. There are n-suitable premice
![]() $\mathcal {N}_k \in \mathcal {F}^+$
for
$\mathcal {N}_k \in \mathcal {F}^+$
for
![]() $k < \omega $
which are cofinal in
$k < \omega $
which are cofinal in
![]() $\mathcal {F}^+$
such that
$\mathcal {F}^+$
such that
![]() $\mathcal {N}_0 = \mathcal {N}$
and for all
$\mathcal {N}_0 = \mathcal {N}$
and for all
![]() $k<\omega $
,
$k<\omega $
,
 $$\begin{align*}M_n(\mathcal{N}_k|\delta^{\mathcal{N}_k}) \vDash \varphi(\bar{\xi}_k,t), \end{align*}$$
$$\begin{align*}M_n(\mathcal{N}_k|\delta^{\mathcal{N}_k}) \vDash \varphi(\bar{\xi}_k,t), \end{align*}$$
where
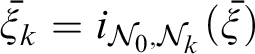 $\bar {\xi }_k = i_{\mathcal {N}_0,\mathcal {N}_k}(\bar {\xi })$
is the image of
$\bar {\xi }_k = i_{\mathcal {N}_0,\mathcal {N}_k}(\bar {\xi })$
is the image of
![]() $\bar {\xi }$
under the iteration map induced by
$\bar {\xi }$
under the iteration map induced by
 $\Sigma _{M_{n+1}^-}$
.
$\Sigma _{M_{n+1}^-}$
.
Proof. By the proof of Lemma 3.35, we can pick a sequence
![]() $(\mathcal {Q}_i \mid i < \omega )$
of premice cofinal in
$(\mathcal {Q}_i \mid i < \omega )$
of premice cofinal in
![]() $\mathcal {F}^+$
such that
$\mathcal {F}^+$
such that
![]() $\mathcal {Q}_i \in \mathcal {F}^{M(y)}$
for all
$\mathcal {Q}_i \in \mathcal {F}^{M(y)}$
for all
![]() $i < \omega $
. Let
$i < \omega $
. Let
![]() $\mathcal {N}_0 = \mathcal {N}$
and construct
$\mathcal {N}_0 = \mathcal {N}$
and construct
![]() $\mathcal {N}_{k+1} \in M(y)$
inductively. Assume that we already constructed
$\mathcal {N}_{k+1} \in M(y)$
inductively. Assume that we already constructed
![]() $\mathcal {N}_k$
and let
$\mathcal {N}_k$
and let
![]() $\mathcal {M} \in M(y)$
be the last model of a correctly guided finite stack on
$\mathcal {M} \in M(y)$
be the last model of a correctly guided finite stack on
![]() $\mathcal {N}$
witnessing that
$\mathcal {N}$
witnessing that
![]() $(b)$
is true. Simultaneously pseudo-coiterate
$(b)$
is true. Simultaneously pseudo-coiterate
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $\mathcal {N}_k$
and
$\mathcal {N}_k$
and
![]() $\mathcal {Q}_k$
to some premouse
$\mathcal {Q}_k$
to some premouse
![]() $\mathcal {N}_k^*$
. Using genericity iterations and Lemma 3.35, there is a pseudo-iterate
$\mathcal {N}_k^*$
. Using genericity iterations and Lemma 3.35, there is a pseudo-iterate
![]() $\mathcal {R}$
of
$\mathcal {R}$
of
![]() $\mathcal {N}_k^*$
such that
$\mathcal {N}_k^*$
such that
![]() $\mathcal {R} \in \mathcal {G} \cap \mathcal {G}^{M(y)}$
(see also Corollary 3.21). In particular, we have by dlm-suitability of
$\mathcal {R} \in \mathcal {G} \cap \mathcal {G}^{M(y)}$
(see also Corollary 3.21). In particular, we have by dlm-suitability of
![]() $M(y)$
that
$M(y)$
that
 $$ \begin{align*} \mathcal{P}^{M(y)}(\mathcal{R}|\delta^{\mathcal{R}}) & = K^{M_n(x)[g]}(\mathcal{R}|\delta^{\mathcal{R}}) = K^{M_n(\mathcal{R}|\delta^{\mathcal{R}})[G][g]}(\mathcal{R}|\delta^{\mathcal{R}}) \\ & = K^{M_n(\mathcal{R}|\delta^{\mathcal{R}})}(\mathcal{R}|\delta^{\mathcal{R}}) = M_n(\mathcal{R}|\delta^{\mathcal{R}}) \end{align*} $$
$$ \begin{align*} \mathcal{P}^{M(y)}(\mathcal{R}|\delta^{\mathcal{R}}) & = K^{M_n(x)[g]}(\mathcal{R}|\delta^{\mathcal{R}}) = K^{M_n(\mathcal{R}|\delta^{\mathcal{R}})[G][g]}(\mathcal{R}|\delta^{\mathcal{R}}) \\ & = K^{M_n(\mathcal{R}|\delta^{\mathcal{R}})}(\mathcal{R}|\delta^{\mathcal{R}}) = M_n(\mathcal{R}|\delta^{\mathcal{R}}) \end{align*} $$
for some G generic over
![]() $M_n(\mathcal {R}|\delta ^{\mathcal {R}})$
for the extender algebra and therefore
$M_n(\mathcal {R}|\delta ^{\mathcal {R}})$
for the extender algebra and therefore
![]() $M_n(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \varphi (i_{\mathcal {N},\mathcal {R}}(\bar {\xi }),t)$
using
$M_n(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \varphi (i_{\mathcal {N},\mathcal {R}}(\bar {\xi }),t)$
using
![]() $(b)$
as
$(b)$
as
 $i_{\mathcal {N},\mathcal {R}}(\bar {\xi }) = \pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi }) = \pi ^{M(y)}_{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi })$
. Moreover,
$i_{\mathcal {N},\mathcal {R}}(\bar {\xi }) = \pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi }) = \pi ^{M(y)}_{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\xi })$
. Moreover,
![]() $\mathcal {R}$
is the last model of a correctly guided finite stack on
$\mathcal {R}$
is the last model of a correctly guided finite stack on
![]() $\mathcal {Q}_k$
and thus
$\mathcal {Q}_k$
and thus
![]() $\mathcal {R} \in \mathcal {F}^+$
, so we can let
$\mathcal {R} \in \mathcal {F}^+$
, so we can let
![]() $\mathcal {N}_{k+1} = \mathcal {R}$
.⊣
$\mathcal {N}_{k+1} = \mathcal {R}$
.⊣
As before we can use this claim to obtain that
which proves
![]() $(a)$
.⊣
$(a)$
.⊣
Let
![]() $\kappa _{\infty }$
be the least inaccessible cardinal above
$\kappa _{\infty }$
be the least inaccessible cardinal above
![]() $\delta _{\infty }$
in
$\delta _{\infty }$
in
 $\hat {\mathcal {M}}_{\infty } = M_n(\mathcal {M}_{\infty }|\delta _{\infty })$
and fix some H which is
$\hat {\mathcal {M}}_{\infty } = M_n(\mathcal {M}_{\infty }|\delta _{\infty })$
and fix some H which is
![]() $\operatorname {Col} (\omega , {<}\kappa _{\infty })$
-generic over
$\operatorname {Col} (\omega , {<}\kappa _{\infty })$
-generic over
![]() $\hat {\mathcal {M}}_{\infty }$
. Then Lemma 4.1 implies for example that
$\hat {\mathcal {M}}_{\infty }$
. Then Lemma 4.1 implies for example that
![]() $\hat {\mathcal {M}}_{\infty }[H]$
and
$\hat {\mathcal {M}}_{\infty }[H]$
and
![]() $M_n(x)[g]$
are elementary equivalent (for formulae in the language of set theory) as for
$M_n(x)[g]$
are elementary equivalent (for formulae in the language of set theory) as for
![]() $\mathcal {R}$
as in the statement of Lemma 4.1, there is some
$\mathcal {R}$
as in the statement of Lemma 4.1, there is some
![]() $\operatorname {Col} (\omega , {<}\kappa ^{\mathcal {R}})$
-generic G, where
$\operatorname {Col} (\omega , {<}\kappa ^{\mathcal {R}})$
-generic G, where
![]() $\kappa ^{\mathcal {R}}$
is the least inaccessible cardinal above
$\kappa ^{\mathcal {R}}$
is the least inaccessible cardinal above
![]() $\delta ^{\mathcal {R}}$
in
$\delta ^{\mathcal {R}}$
in
 $\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}})$
, such that
$\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}})$
, such that
 $\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}})[G] = M_n(x)[g]$
.
$\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}})[G] = M_n(x)[g]$
.
We defined a direct limit system
![]() $\mathcal {F}^{M(y)}$
for all dlm-suitable
$\mathcal {F}^{M(y)}$
for all dlm-suitable
![]() $M(y)$
in
$M(y)$
in
![]() $M_n(x)[g]$
. Therefore, there is a direct limit system
$M_n(x)[g]$
. Therefore, there is a direct limit system
![]() $\mathcal {F}^{*, M(y)}$
with the same properties for each dlm-suitable
$\mathcal {F}^{*, M(y)}$
with the same properties for each dlm-suitable
![]() $M(y)$
in
$M(y)$
in
![]() $\hat {\mathcal {M}}_{\infty }[H]$
(adapting the definition of dlm-suitable to
$\hat {\mathcal {M}}_{\infty }[H]$
(adapting the definition of dlm-suitable to
![]() $\hat {\mathcal {M}}_{\infty }[H]$
). It is easy to see that Lemma 4.1 implies that for each
$\hat {\mathcal {M}}_{\infty }[H]$
). It is easy to see that Lemma 4.1 implies that for each
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
there is a
$s \in [\operatorname {Ord} ]^{<\omega }$
there is a
![]() $y_s$
such that
$y_s$
such that
![]() $\mathcal {M}_{\infty } \in \mathcal {G}^{M(y_s)}$
and
$\mathcal {M}_{\infty } \in \mathcal {G}^{M(y_s)}$
and
![]() $\mathcal {M}_{\infty }$
is strongly
$\mathcal {M}_{\infty }$
is strongly
![]() $s^*$
-iterable in
$s^*$
-iterable in
![]() $M(y_s)$
in
$M(y_s)$
in
![]() $\hat {\mathcal {M}}_{\infty }[H]$
. In fact, the direct limit embedding
$\hat {\mathcal {M}}_{\infty }[H]$
. In fact, the direct limit embedding
 $(\pi _{(\mathcal {M}_{\infty },s^*),\infty }^{M(y_s)})^{\mathcal {F}^{*, M(y_s)}}$
in the system
$(\pi _{(\mathcal {M}_{\infty },s^*),\infty }^{M(y_s)})^{\mathcal {F}^{*, M(y_s)}}$
in the system
![]() $\mathcal {F}^{*, M(y_s)}$
is independent of the choice of
$\mathcal {F}^{*, M(y_s)}$
is independent of the choice of
![]() $y_s$
and we can consider
$y_s$
and we can consider
 $$ \begin{align*} \pi_{\infty} & = \bigcup \left\{ \left(\pi_{(\mathcal{M}_{\infty},s^*),\infty}^{M(y_s)}\right)^{\mathcal{F}^{*, M(y_s)}} \mid s \in [\operatorname{Ord} ]^{<\omega} \text{ and } y_s \text{ is such that } \right.\\ & \left.\mathcal{M}_{\infty} \in \mathcal{G}^{M(y_s)} \text{ and } \mathcal{M}_{\infty} \text{ is strongly } s^*\text{-iterable in } M(y_s) \text{ in } \hat{\mathcal{M}}_{\infty}[H] \vphantom{\left(\pi_{(\mathcal{M}_{\infty},s^*),\infty}^{M(y_s)}\right)^{\mathcal{F}^{*, M(y_s)}}}\right\}. \end{align*} $$
$$ \begin{align*} \pi_{\infty} & = \bigcup \left\{ \left(\pi_{(\mathcal{M}_{\infty},s^*),\infty}^{M(y_s)}\right)^{\mathcal{F}^{*, M(y_s)}} \mid s \in [\operatorname{Ord} ]^{<\omega} \text{ and } y_s \text{ is such that } \right.\\ & \left.\mathcal{M}_{\infty} \in \mathcal{G}^{M(y_s)} \text{ and } \mathcal{M}_{\infty} \text{ is strongly } s^*\text{-iterable in } M(y_s) \text{ in } \hat{\mathcal{M}}_{\infty}[H] \vphantom{\left(\pi_{(\mathcal{M}_{\infty},s^*),\infty}^{M(y_s)}\right)^{\mathcal{F}^{*, M(y_s)}}}\right\}. \end{align*} $$
Lemma 4.2. For all
![]() $\eta < \delta _{\infty }$
we have that
$\eta < \delta _{\infty }$
we have that
![]() $\pi _{\infty }(\eta ) = \eta ^*$
.
$\pi _{\infty }(\eta ) = \eta ^*$
.
Proof. This is again a consequence of Lemma 4.1. Consider the dlm-suitable premouse
![]() $M_n(x)$
. Let
$M_n(x)$
. Let
![]() $\eta = \pi _{(\mathcal {N},s),\infty }(\bar {\eta })$
for some
$\eta = \pi _{(\mathcal {N},s),\infty }(\bar {\eta })$
for some
![]() $(\mathcal {N},s) \in \mathcal {I}$
and
$(\mathcal {N},s) \in \mathcal {I}$
and
![]() $\bar {\eta } < \gamma _s^{\mathcal {N}}$
and consider the formula
$\bar {\eta } < \gamma _s^{\mathcal {N}}$
and consider the formula

where
![]() $\kappa ^*$
refers to the least inaccessible cardinal above the least Woodin cardinal of the current model. Recall that for any dlm-suitable y and z witnessed by
$\kappa ^*$
refers to the least inaccessible cardinal above the least Woodin cardinal of the current model. Recall that for any dlm-suitable y and z witnessed by
![]() $M(y)$
and
$M(y)$
and
![]() $M(z)$
, for any
$M(z)$
, for any
![]() $(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}^{M(y)} \cap \mathcal {I}^{M(z)}$
with
$(\mathcal {N},s), (\mathcal {M},t) \in \mathcal {I}^{M(y)} \cap \mathcal {I}^{M(z)}$
with
![]() $(\mathcal {N},s) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
and
$(\mathcal {N},s) \leq _{\mathcal {I}^{M(y)}} (\mathcal {M},t)$
and
![]() $(\mathcal {N},s) \leq _{\mathcal {I}^{M(z)}} (\mathcal {M},t)$
the induced embeddings
$(\mathcal {N},s) \leq _{\mathcal {I}^{M(z)}} (\mathcal {M},t)$
the induced embeddings
 $\pi _{(\mathcal {N},s),(\mathcal {M},t)}^{M(y)}$
and
$\pi _{(\mathcal {N},s),(\mathcal {M},t)}^{M(y)}$
and
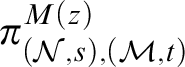 $\pi _{(\mathcal {N},s),(\mathcal {M},t)}^{M(z)}$
agree. Hence, in
$\pi _{(\mathcal {N},s),(\mathcal {M},t)}^{M(z)}$
agree. Hence, in
![]() $M_n(x)[g]$
, we have for every
$M_n(x)[g]$
, we have for every
![]() $\mathcal {R} \in \mathcal {G}$
which is the last model of a correctly guided finite stack on
$\mathcal {R} \in \mathcal {G}$
which is the last model of a correctly guided finite stack on
![]() $\mathcal {N}$
that for all dlm-suitable y such that
$\mathcal {N}$
that for all dlm-suitable y such that
![]() $\mathcal {R} \in \mathcal {G}^{M(y)}$
, in fact
$\mathcal {R} \in \mathcal {G}^{M(y)}$
, in fact
![]() $(\mathcal {R},s) \in \mathcal {I}^{M(y)}$
,
$(\mathcal {R},s) \in \mathcal {I}^{M(y)}$
,
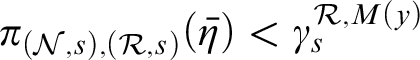 $\pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\eta }) < \gamma _{s}^{\mathcal {R}, M(y)}$
, and
$\pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\eta }) < \gamma _{s}^{\mathcal {R}, M(y)}$
, and
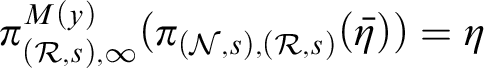 $\pi _{(\mathcal {R},s),\infty }^{M(y)}(\pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\eta })) = \eta $
. Therefore,
$\pi _{(\mathcal {R},s),\infty }^{M(y)}(\pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\eta })) = \eta $
. Therefore,
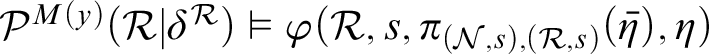 $\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \varphi (\mathcal {R}, s, \pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\eta }), \eta )$
. So Lemma 4.1 yields that
$\mathcal {P}^{M(y)}(\mathcal {R}|\delta ^{\mathcal {R}}) \vDash \varphi (\mathcal {R}, s, \pi _{(\mathcal {N},s),(\mathcal {R},s)}(\bar {\eta }), \eta )$
. So Lemma 4.1 yields that
![]() $\hat {\mathcal {M}}_{\infty } \vDash \varphi (\mathcal {M}_{\infty }, s^*, \eta , \eta ^*)$
. So in
$\hat {\mathcal {M}}_{\infty } \vDash \varphi (\mathcal {M}_{\infty }, s^*, \eta , \eta ^*)$
. So in
![]() $\hat {\mathcal {M}}_{\infty }[H]$
, for all dlm-suitable y with
$\hat {\mathcal {M}}_{\infty }[H]$
, for all dlm-suitable y with
![]() $\mathcal {M}_{\infty } \in \mathcal {G}^{M(y)}$
, we have
$\mathcal {M}_{\infty } \in \mathcal {G}^{M(y)}$
, we have
![]() $(\mathcal {M}_{\infty },s^*) \in \mathcal {I}^{M(y)}$
and
$(\mathcal {M}_{\infty },s^*) \in \mathcal {I}^{M(y)}$
and
 $(\pi ^{M(y)}_{(\mathcal {M}_{\infty },s^*),\infty })^{\mathcal {F}^*, M(y)}(\eta ) = \eta ^*$
, as desired.⊣
$(\pi ^{M(y)}_{(\mathcal {M}_{\infty },s^*),\infty })^{\mathcal {F}^*, M(y)}(\eta ) = \eta ^*$
, as desired.⊣
Theorem 4.3.
 $V_{\delta _{\infty }}^{\operatorname {HOD}^{M_n(x)[g]} } = V_{\delta _{\infty }}^{\mathcal {M}_{\infty }}$
.
$V_{\delta _{\infty }}^{\operatorname {HOD}^{M_n(x)[g]} } = V_{\delta _{\infty }}^{\mathcal {M}_{\infty }}$
.
Proof. By the internal definition of
![]() $\mathcal {M}_{\infty }$
from Lemma 3.35 we have that
$\mathcal {M}_{\infty }$
from Lemma 3.35 we have that
 $V_{\delta _{\infty }}^{\mathcal {M}_{\infty }} \subseteq V_{\delta _{\infty }}^{\operatorname {HOD}^{M_n(x)[g]} }$
. For the other inclusion we first show the following claim.
$V_{\delta _{\infty }}^{\mathcal {M}_{\infty }} \subseteq V_{\delta _{\infty }}^{\operatorname {HOD}^{M_n(x)[g]} }$
. For the other inclusion we first show the following claim.
Claim 1.
![]() $\pi _{\infty } \upharpoonright \alpha \in \hat {\mathcal {M}}_{\infty }$
for all
$\pi _{\infty } \upharpoonright \alpha \in \hat {\mathcal {M}}_{\infty }$
for all
![]() $\alpha < \delta _{\infty }$
.
$\alpha < \delta _{\infty }$
.
Proof. As
![]() $\alpha < \delta _{\infty }$
, there exists an
$\alpha < \delta _{\infty }$
, there exists an
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
and a dlm-suitable
$s \in [\operatorname {Ord} ]^{<\omega }$
and a dlm-suitable
![]() $y_s$
such that, in
$y_s$
such that, in
![]() $\hat {\mathcal {M}}_{\infty }[H]$
,
$\hat {\mathcal {M}}_{\infty }[H]$
,
![]() $\mathcal {M}_{\infty } \in \mathcal {G}^{M(y)}$
and
$\mathcal {M}_{\infty } \in \mathcal {G}^{M(y)}$
and
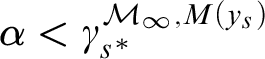 $\alpha < \gamma _{s^*}^{\mathcal {M}_{\infty }, M(y_s)}$
. We have by definition that
$\alpha < \gamma _{s^*}^{\mathcal {M}_{\infty }, M(y_s)}$
. We have by definition that
 $\pi _{\infty } \upharpoonright \alpha = (\pi ^{M(y_s)}_{(\mathcal {M}_{\infty },s^*),\infty })^{\mathcal {F}^*, M(y_s)} \upharpoonright \alpha $
. As
$\pi _{\infty } \upharpoonright \alpha = (\pi ^{M(y_s)}_{(\mathcal {M}_{\infty },s^*),\infty })^{\mathcal {F}^*, M(y_s)} \upharpoonright \alpha $
. As
 $ (\pi ^{M(y_s)}_{(\mathcal {M}_{\infty },s^*),\infty })^{\mathcal {F}^*, M(y_s)} \upharpoonright \alpha $
does not depend on the choice of
$ (\pi ^{M(y_s)}_{(\mathcal {M}_{\infty },s^*),\infty })^{\mathcal {F}^*, M(y_s)} \upharpoonright \alpha $
does not depend on the choice of
![]() $y_s$
, this implies
$y_s$
, this implies
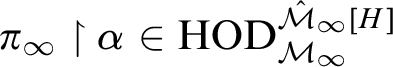 $\pi _{\infty } \upharpoonright \alpha \in \operatorname {HOD} ^{\hat {\mathcal {M}}_{\infty }[H]}_{\mathcal {M}_{\infty }}$
and thus
$\pi _{\infty } \upharpoonright \alpha \in \operatorname {HOD} ^{\hat {\mathcal {M}}_{\infty }[H]}_{\mathcal {M}_{\infty }}$
and thus
![]() $\pi _{\infty } \upharpoonright \alpha \in \hat {\mathcal {M}}_{\infty }$
by homogeneity of the forcing
$\pi _{\infty } \upharpoonright \alpha \in \hat {\mathcal {M}}_{\infty }$
by homogeneity of the forcing
![]() $\mathbb {P} = \operatorname {Col} (\omega , {<}\kappa _{\infty })$
.⊣
$\mathbb {P} = \operatorname {Col} (\omega , {<}\kappa _{\infty })$
.⊣
Now let
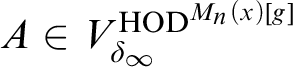 $A \in V_{\delta _{\infty }}^{\operatorname {HOD}^{M_n(x)[g]} }$
be arbitrary. Let
$A \in V_{\delta _{\infty }}^{\operatorname {HOD}^{M_n(x)[g]} }$
be arbitrary. Let
![]() $\alpha < \delta _{\infty }$
be such that
$\alpha < \delta _{\infty }$
be such that
![]() $A \subset \alpha $
is defined over
$A \subset \alpha $
is defined over
![]() $M_n(x)[g]$
by a formula
$M_n(x)[g]$
by a formula
![]() $\varphi $
with ordinal parameters from
$\varphi $
with ordinal parameters from
![]() $t \in [\operatorname {Ord} ]^{<\omega }$
and let
$t \in [\operatorname {Ord} ]^{<\omega }$
and let
![]() $\beta < \alpha $
be arbitrary. That means
$\beta < \alpha $
be arbitrary. That means
![]() $\beta \in A$
iff
$\beta \in A$
iff
![]() $M_n(x)[g] \vDash \varphi (\beta ,t)$
. Lemma 4.1 yields that this is the case iff
$M_n(x)[g] \vDash \varphi (\beta ,t)$
. Lemma 4.1 yields that this is the case iff
![]() $\hat {\mathcal {M}}_{\infty }[H] \vDash \varphi (\beta ^*, t^*)$
. Since
$\hat {\mathcal {M}}_{\infty }[H] \vDash \varphi (\beta ^*, t^*)$
. Since
![]() $\beta < \alpha < \delta _{\infty }$
, we have that
$\beta < \alpha < \delta _{\infty }$
, we have that
![]() $\beta ^* = \pi _{\infty }(\beta )$
by Lemma 4.2. Moreover, we have by Claim 1 that
$\beta ^* = \pi _{\infty }(\beta )$
by Lemma 4.2. Moreover, we have by Claim 1 that
![]() $\pi _{\infty } \upharpoonright \alpha \in \hat {\mathcal {M}}_{\infty }$
. Therefore, it follows by homogeneity of the forcing
$\pi _{\infty } \upharpoonright \alpha \in \hat {\mathcal {M}}_{\infty }$
. Therefore, it follows by homogeneity of the forcing
![]() $\mathbb {P} = \operatorname {Col} (\omega , {<}\kappa _{\infty })$
that
$\mathbb {P} = \operatorname {Col} (\omega , {<}\kappa _{\infty })$
that
![]() $A \in \hat {\mathcal {M}}_{\infty }$
since
$A \in \hat {\mathcal {M}}_{\infty }$
since
![]() $t^*$
is a fixed parameter in
$t^*$
is a fixed parameter in
![]() $\hat {\mathcal {M}}_{\infty }$
. Thus
$\hat {\mathcal {M}}_{\infty }$
. Thus
 $A \in V_{\delta _{\infty }}^{\mathcal {M}_{\infty }}$
, as desired.⊣
$A \in V_{\delta _{\infty }}^{\mathcal {M}_{\infty }}$
, as desired.⊣
5 The full
 $\operatorname {HOD} $
in
$\operatorname {HOD} $
in
 $M_n(x)[g]$
$M_n(x)[g]$
To compute the full model
![]() $\operatorname {HOD}^{M_n(x)[g]} $
, i.e., prove Theorem 1.1, we first show the following lemma. Recall that
$\operatorname {HOD}^{M_n(x)[g]} $
, i.e., prove Theorem 1.1, we first show the following lemma. Recall that
 $\omega _2^{M_n(x)[g]} = \delta _{\infty }$
.
$\omega _2^{M_n(x)[g]} = \delta _{\infty }$
.
Lemma 5.1.
 $\operatorname {HOD}^{M_n(x)[g]} = M_n(A)$
for some set
$\operatorname {HOD}^{M_n(x)[g]} = M_n(A)$
for some set
 $A \subseteq \omega _2^{M_n(x)[g]}$
with
$A \subseteq \omega _2^{M_n(x)[g]}$
with
![]() $A \in \operatorname {HOD}^{M_n(x)[g]} $
.
$A \in \operatorname {HOD}^{M_n(x)[g]} $
.
Proof. Let
![]() $\mathbb {V}$
denote the Vopěnka algebra in
$\mathbb {V}$
denote the Vopěnka algebra in
![]() $M_n(x)[g]$
for making a real generic over
$M_n(x)[g]$
for making a real generic over
![]() $\operatorname {HOD}^{M_n(x)[g]} $
. By Vopěnka’s theorem (see for example Theorem 15.46 in [Reference Jech4] or Theorem 9.0.1 in [Reference Larson6]) there is a
$\operatorname {HOD}^{M_n(x)[g]} $
. By Vopěnka’s theorem (see for example Theorem 15.46 in [Reference Jech4] or Theorem 9.0.1 in [Reference Larson6]) there is a
![]() $\mathbb {V}$
-generic
$\mathbb {V}$
-generic
![]() $G_x$
over
$G_x$
over
![]() $\operatorname {HOD}^{M_n(x)[g]} $
such that
$\operatorname {HOD}^{M_n(x)[g]} $
such that
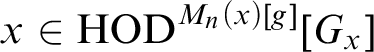 $x \in \operatorname {HOD}^{M_n(x)[g]} [G_x]$
and in fact
$x \in \operatorname {HOD}^{M_n(x)[g]} [G_x]$
and in fact
 $\operatorname {HOD}^{M_n(x)[g]} [G_x] = \operatorname {HOD}^{M_n(x)[g]} _x$
.
$\operatorname {HOD}^{M_n(x)[g]} [G_x] = \operatorname {HOD}^{M_n(x)[g]} _x$
.
Claim 1. There is some
![]() $\tilde {\mathbb {V}} \in \operatorname {HOD}^{M_n(x)[g]} $
which is isomorphic to
$\tilde {\mathbb {V}} \in \operatorname {HOD}^{M_n(x)[g]} $
which is isomorphic to
![]() $\mathbb {V}$
and a subset of
$\mathbb {V}$
and a subset of
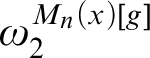 $\omega _2^{M_n(x)[g]}$
.Footnote
7
$\omega _2^{M_n(x)[g]}$
.Footnote
7
Proof. Work in
![]() $M_n(x)[g]$
. Each real, i.e., element of
$M_n(x)[g]$
. Each real, i.e., element of
![]() $\mathcal {P}(\omega )$
, can be coded by a countable ordinal and each set of reals can be coded by an ordinal
$\mathcal {P}(\omega )$
, can be coded by a countable ordinal and each set of reals can be coded by an ordinal
![]() $< \omega _2$
. Forcing with the Vopěnka algebra
$< \omega _2$
. Forcing with the Vopěnka algebra
![]() $\mathbb {V}$
is
$\mathbb {V}$
is
![]() $\omega _2$
-c.c. in
$\omega _2$
-c.c. in
![]() $M_n(x)[g]$
as otherwise there would be an
$M_n(x)[g]$
as otherwise there would be an
![]() $\omega _2$
sequence of pairwise distinct non-empty sets of reals, contradicting
$\omega _2$
sequence of pairwise distinct non-empty sets of reals, contradicting
![]() $\operatorname {CH} $
. The Vopěnka algebra is in
$\operatorname {CH} $
. The Vopěnka algebra is in
![]() $\operatorname {HOD}^{M_n(x)[g]} $
and when considering
$\operatorname {HOD}^{M_n(x)[g]} $
and when considering
 $\operatorname {HOD}^{M_n(x)[g]} [G_x]$
cardinals
$\operatorname {HOD}^{M_n(x)[g]} [G_x]$
cardinals
![]() $\geq (\kappa ^+)^{M_n(x)}$
are preserved. Since
$\geq (\kappa ^+)^{M_n(x)}$
are preserved. Since
![]() $(\kappa ^{+\omega })^{M_n(x)}$
is below the least measurable cardinal of
$(\kappa ^{+\omega })^{M_n(x)}$
is below the least measurable cardinal of
![]() $M_n(x)$
,
$M_n(x)$
,
 $M_n(x)|(\kappa ^{+\omega })^{M_n(x)}$
can be written as the
$M_n(x)|(\kappa ^{+\omega })^{M_n(x)}$
can be written as the
![]() $Lp^n$
-stack of height
$Lp^n$
-stack of height
![]() $(\kappa ^{+\omega })^{M_n(x)}$
above x and is therefore by the argument in Lemma 3.18 an element of
$(\kappa ^{+\omega })^{M_n(x)}$
above x and is therefore by the argument in Lemma 3.18 an element of
 $\operatorname {HOD}^{M_n(x)[g]} _x = \operatorname {HOD}^{M_n(x)[g]} [G_x]$
. But the Vopěnka algebra is a subset of some ordinal
$\operatorname {HOD}^{M_n(x)[g]} _x = \operatorname {HOD}^{M_n(x)[g]} [G_x]$
. But the Vopěnka algebra is a subset of some ordinal
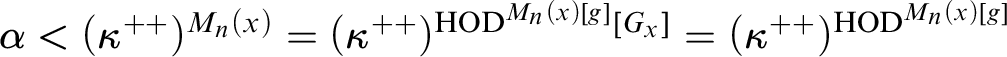 $\alpha < (\kappa ^{++})^{M_n(x)} = (\kappa ^{++})^{\operatorname {HOD}^{M_n(x)[g]} [G_x]} = (\kappa ^{++})^{\operatorname {HOD}^{M_n(x)[g]} }$
, so there is some
$\alpha < (\kappa ^{++})^{M_n(x)} = (\kappa ^{++})^{\operatorname {HOD}^{M_n(x)[g]} [G_x]} = (\kappa ^{++})^{\operatorname {HOD}^{M_n(x)[g]} }$
, so there is some
![]() $\tilde {\mathbb {V}} \in \operatorname {HOD}^{M_n(x)[g]} $
which is isomorphic to
$\tilde {\mathbb {V}} \in \operatorname {HOD}^{M_n(x)[g]} $
which is isomorphic to
![]() $\mathbb {V}$
and a subset of
$\mathbb {V}$
and a subset of
![]() $(\kappa ^+)^{M_n(x)}$
.⊣
$(\kappa ^+)^{M_n(x)}$
.⊣
For the rest of this proof we write
![]() $\mathbb {V}$
for the
$\mathbb {V}$
for the
![]() $\tilde {\mathbb {V}}$
from the previous claim and show that
$\tilde {\mathbb {V}}$
from the previous claim and show that
 $M_n(\mathbb {V}) = \operatorname {HOD}^{M_n(x)[g]} $
.
$M_n(\mathbb {V}) = \operatorname {HOD}^{M_n(x)[g]} $
.
Claim 2.
![]() $G_x$
is
$G_x$
is
![]() $\mathbb {V}$
-generic over
$\mathbb {V}$
-generic over
![]() $M_n(\mathbb {V})$
.
$M_n(\mathbb {V})$
.
Proof. The dense sets in question are elements of
![]() $\mathcal {P}(\mathbb {V})^{M_n(\mathbb {V})}$
and hence elements of
$\mathcal {P}(\mathbb {V})^{M_n(\mathbb {V})}$
and hence elements of
![]() $Lp^n(\mathbb {V}) \kern1.2pt{=}\kern1.2pt \bigcup \{N \, | \, N \text { is a countable } \mathbb {V}\text {-premouse with } \rho _{\omega }(N) \kern1.2pt{=}\kern1.2pt \mathbb {V} \text { which is } n\text {-small,} \text{sound, and }(\omega ,\omega _1,\omega _1)\text {-iterable}\}$
. As
$Lp^n(\mathbb {V}) \kern1.2pt{=}\kern1.2pt \bigcup \{N \, | \, N \text { is a countable } \mathbb {V}\text {-premouse with } \rho _{\omega }(N) \kern1.2pt{=}\kern1.2pt \mathbb {V} \text { which is } n\text {-small,} \text{sound, and }(\omega ,\omega _1,\omega _1)\text {-iterable}\}$
. As
![]() $\mathbb {V} \in \operatorname {HOD}^{M_n(x)[g]} $
, Lemma 3.18 yields that
$\mathbb {V} \in \operatorname {HOD}^{M_n(x)[g]} $
, Lemma 3.18 yields that
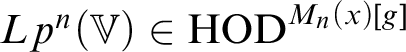 $Lp^n(\mathbb {V}) \in \operatorname {HOD}^{M_n(x)[g]} $
, which implies the claim.⊣
$Lp^n(\mathbb {V}) \in \operatorname {HOD}^{M_n(x)[g]} $
, which implies the claim.⊣
Let
![]() $\lambda $
be the least inaccessible of
$\lambda $
be the least inaccessible of
![]() $M_n(x)$
above
$M_n(x)$
above
![]() $\kappa $
.
$\kappa $
.
Claim 3.
 $V_{\lambda }^{M_n(x)} = V_{\lambda }^{M_n(\mathbb {V})[G_x]}$
and
$V_{\lambda }^{M_n(x)} = V_{\lambda }^{M_n(\mathbb {V})[G_x]}$
and
![]() $\lambda $
is a cardinal in
$\lambda $
is a cardinal in
![]() $M_n(\mathbb {V})[G_x]$
.
$M_n(\mathbb {V})[G_x]$
.
Proof. Write
 $\kappa _0^{M_n(x)}$
and
$\kappa _0^{M_n(x)}$
and
 $\kappa _0^{M_n(\mathbb {V})}$
for the least measurable cardinal of
$\kappa _0^{M_n(\mathbb {V})}$
for the least measurable cardinal of
![]() $M_n(x)$
and
$M_n(x)$
and
![]() $M_n(\mathbb {V})$
respectively.
$M_n(\mathbb {V})$
respectively.
![]() $M_n(\mathbb {V})$
and
$M_n(\mathbb {V})$
and
![]() $M_n(\mathbb {V})[G_x]$
have the same least measurable cardinal. The proof of Lemma 3.18 shows that
$M_n(\mathbb {V})[G_x]$
have the same least measurable cardinal. The proof of Lemma 3.18 shows that
![]() $Lp^n(z) \in M_n(\mathbb {V})[G_x]$
for any
$Lp^n(z) \in M_n(\mathbb {V})[G_x]$
for any
 $z \in V_{\delta _0}^{M_n(\mathbb {V})[G_x]}$
, where
$z \in V_{\delta _0}^{M_n(\mathbb {V})[G_x]}$
, where
![]() $\delta _0$
denotes the least Woodin cardinal in
$\delta _0$
denotes the least Woodin cardinal in
![]() $M_n(\mathbb {V})[G_x]$
. As
$M_n(\mathbb {V})[G_x]$
. As
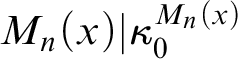 $M_n(x)|\kappa _0^{M_n(x)}$
is equal to the
$M_n(x)|\kappa _0^{M_n(x)}$
is equal to the
![]() $Lp^n$
-stack of height
$Lp^n$
-stack of height
 $\kappa _0^{M_n(x)}$
over x, it follows that
$\kappa _0^{M_n(x)}$
over x, it follows that
 $$\begin{align*}M_n(x)|\kappa_0^{M_n(x)} \subseteq M_n(\mathbb{V})[G_x]. \end{align*}$$
$$\begin{align*}M_n(x)|\kappa_0^{M_n(x)} \subseteq M_n(\mathbb{V})[G_x]. \end{align*}$$
Analogously,
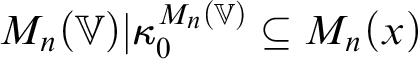 $M_n(\mathbb {V})|\kappa _0^{M_n(\mathbb {V})} \subseteq M_n(x)$
and in fact
$M_n(\mathbb {V})|\kappa _0^{M_n(\mathbb {V})} \subseteq M_n(x)$
and in fact
 $$\begin{align*}M_n(\mathbb{V})[G_x]|\kappa_0^{M_n(\mathbb{V})} \subseteq M_n(x). \end{align*}$$
$$\begin{align*}M_n(\mathbb{V})[G_x]|\kappa_0^{M_n(\mathbb{V})} \subseteq M_n(x). \end{align*}$$
We are left with showing that
 $\lambda < \kappa _0^{M_n(\mathbb {V})}$
(as
$\lambda < \kappa _0^{M_n(\mathbb {V})}$
(as
 $\lambda < \kappa _0^{M_n(x)}$
is obvious). So suppose toward a contradiction that
$\lambda < \kappa _0^{M_n(x)}$
is obvious). So suppose toward a contradiction that
 $\lambda \geq \kappa _0^{M_n(\mathbb {V})}$
. Then
$\lambda \geq \kappa _0^{M_n(\mathbb {V})}$
. Then
 $$\begin{align*}V_{\kappa_0^{M_n(\mathbb{V})}}^{M_n(\mathbb{V})[G_x]} = V_{\kappa_0^{M_n(\mathbb{V})}}^{M_n(x)}. \end{align*}$$
$$\begin{align*}V_{\kappa_0^{M_n(\mathbb{V})}}^{M_n(\mathbb{V})[G_x]} = V_{\kappa_0^{M_n(\mathbb{V})}}^{M_n(x)}. \end{align*}$$
Therefore,
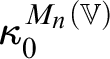 $\kappa _0^{M_n(\mathbb {V})}$
is not only a limit of inaccessible cardinals in
$\kappa _0^{M_n(\mathbb {V})}$
is not only a limit of inaccessible cardinals in
![]() $M_n(\mathbb {V})[G_x]$
but also in
$M_n(\mathbb {V})[G_x]$
but also in
![]() $M_n(x)$
, contradicting our assumption that
$M_n(x)$
, contradicting our assumption that
 $\lambda \geq \kappa _0^{M_n(\mathbb {V})}$
.⊣
$\lambda \geq \kappa _0^{M_n(\mathbb {V})}$
.⊣
Claim 4.
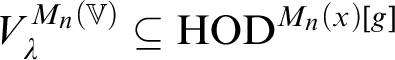 $V_{\lambda }^{M_n(\mathbb {V})} \subseteq \operatorname {HOD}^{M_n(x)[g]} $
.
$V_{\lambda }^{M_n(\mathbb {V})} \subseteq \operatorname {HOD}^{M_n(x)[g]} $
.
Proof. This follows from the proof of Lemma 3.18 as
![]() $M_n(\mathbb {V})|\lambda $
can be obtained as the
$M_n(\mathbb {V})|\lambda $
can be obtained as the
![]() $Lp^n$
-stack of height
$Lp^n$
-stack of height
![]() $\lambda $
over
$\lambda $
over
![]() $\mathbb {V}$
and
$\mathbb {V}$
and
![]() $\mathbb {V} \in \operatorname {HOD}^{M_n(x)[g]} $
.⊣
$\mathbb {V} \in \operatorname {HOD}^{M_n(x)[g]} $
.⊣
Now we can show that the lemma holds below
![]() $\lambda $
.
$\lambda $
.
Claim 5.
 $V_{\lambda }^{M_n(\mathbb {V})} = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
.
$V_{\lambda }^{M_n(\mathbb {V})} = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
.
Proof. We first show that
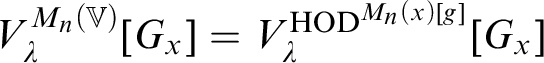 $V_{\lambda }^{M_n(\mathbb {V})}[G_x] = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }[G_x]$
. The inclusion
$V_{\lambda }^{M_n(\mathbb {V})}[G_x] = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }[G_x]$
. The inclusion
![]() $\subseteq $
follows from Claim 4. For the other inclusion we have that
$\subseteq $
follows from Claim 4. For the other inclusion we have that
 $$\begin{align*}\operatorname{HOD} ^{M_n(x)[g]}[G_x] = \operatorname{HOD} _x^{M_n(x)[g]} \subseteq \operatorname{HOD} _x^{M_n(x)} \subseteq M_n(x), \end{align*}$$
$$\begin{align*}\operatorname{HOD} ^{M_n(x)[g]}[G_x] = \operatorname{HOD} _x^{M_n(x)[g]} \subseteq \operatorname{HOD} _x^{M_n(x)} \subseteq M_n(x), \end{align*}$$
using the homogeneity and ordinal definability of the forcing
![]() $\operatorname {Col} (\omega , {<}\kappa )$
. Therefore by Claim 3
$\operatorname {Col} (\omega , {<}\kappa )$
. Therefore by Claim 3
 $$\begin{align*}V_{\lambda}^{\operatorname{HOD}^{M_n(x)[g]} }[G_x] \subseteq V_{\lambda}^{M_n(x)} = V_{\lambda}^{M_n(\mathbb{V})}[G_x]. \end{align*}$$
$$\begin{align*}V_{\lambda}^{\operatorname{HOD}^{M_n(x)[g]} }[G_x] \subseteq V_{\lambda}^{M_n(x)} = V_{\lambda}^{M_n(\mathbb{V})}[G_x]. \end{align*}$$
Finally, we argue that the equality
 $V_{\lambda }^{M_n(\mathbb {V})}[G_x] = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }[G_x]$
also holds true without adding the generic
$V_{\lambda }^{M_n(\mathbb {V})}[G_x] = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }[G_x]$
also holds true without adding the generic
![]() $G_x$
. As by Claim 4 we have
$G_x$
. As by Claim 4 we have
 $V_{\lambda }^{M_n(\mathbb {V})} \subseteq V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
, we are again left with proving the other inclusion. Let
$V_{\lambda }^{M_n(\mathbb {V})} \subseteq V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
, we are again left with proving the other inclusion. Let
![]() $\mathbb {P} = \mathbb {V} \times \operatorname {Col} (\omega ,{<}\kappa )$
. Then
$\mathbb {P} = \mathbb {V} \times \operatorname {Col} (\omega ,{<}\kappa )$
. Then
![]() $(G_x,g)$
is
$(G_x,g)$
is
![]() $\mathbb {P}$
-generic over both
$\mathbb {P}$
-generic over both
 $V_{\lambda }^{M_n(\mathbb {V})}$
and
$V_{\lambda }^{M_n(\mathbb {V})}$
and
 $V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
, and
$V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
, and
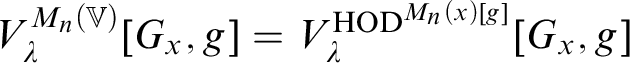 $V_{\lambda }^{M_n(\mathbb {V})}[G_x,g] = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }[G_x,g]$
. Let
$V_{\lambda }^{M_n(\mathbb {V})}[G_x,g] = V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }[G_x,g]$
. Let
 $a \in V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
be a set of ordinals. Then there is a
$a \in V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
be a set of ordinals. Then there is a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
 $\sigma \kern1.2pt{\in}\kern1.2pt V_{\lambda }^{M_n(\mathbb {V})}$
such that
$\sigma \kern1.2pt{\in}\kern1.2pt V_{\lambda }^{M_n(\mathbb {V})}$
such that
![]() $\sigma _{(G_x,g)} \kern1.2pt{=}\kern1.2pt a$
. This is forced over
$\sigma _{(G_x,g)} \kern1.2pt{=}\kern1.2pt a$
. This is forced over
 $V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
, i.e., there is a
$V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} }$
, i.e., there is a
![]() $p \in \mathbb {P}$
such that
$p \in \mathbb {P}$
such that
 .” Thus
.” Thus
 $V_{\lambda }^{M_n(\mathbb {V})}$
can compute the elements of a using the forcing relation for
$V_{\lambda }^{M_n(\mathbb {V})}$
can compute the elements of a using the forcing relation for
![]() $\mathbb {P}$
below p. Hence
$\mathbb {P}$
below p. Hence
 $a \in V_{\lambda }^{M_n(\mathbb {V})}$
, as desired.⊣
$a \in V_{\lambda }^{M_n(\mathbb {V})}$
, as desired.⊣
Now we are able to extend Claim 3 to the full models.
Claim 6.
![]() $M_n(\mathbb {V})[G_x] = M_n(x)$
.
$M_n(\mathbb {V})[G_x] = M_n(x)$
.
Proof. Consider
![]() $M_n(x)[g]$
as a
$M_n(x)[g]$
as a
 $V_{\lambda }^{M_n(x)[g]}$
-premouse and note that it equals
$V_{\lambda }^{M_n(x)[g]}$
-premouse and note that it equals
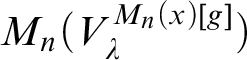 $M_n(V_{\lambda }^{M_n(x)[g]})$
. We use
$M_n(V_{\lambda }^{M_n(x)[g]})$
. We use
 $\mathcal {P}^{M_n(x)[g]}(M_n(\mathbb {V})|\lambda )$
to denote the result of a
$\mathcal {P}^{M_n(x)[g]}(M_n(\mathbb {V})|\lambda )$
to denote the result of a
![]() $\mathcal {P}$
-construction in the sense of [Reference Schindler and Steel15] above
$\mathcal {P}$
-construction in the sense of [Reference Schindler and Steel15] above
![]() $M_n(\mathbb {V})|\lambda $
inside the
$M_n(\mathbb {V})|\lambda $
inside the
 $V_{\lambda }^{M_n(x)[g]}$
-premouse
$V_{\lambda }^{M_n(x)[g]}$
-premouse
![]() $M_n(x)[g]$
. By Claim 3,
$M_n(x)[g]$
. By Claim 3,
 $V_{\lambda }^{M_n(\mathbb {V})}[G_x] = V_{\lambda }^{M_n(x)}$
, so
$V_{\lambda }^{M_n(\mathbb {V})}[G_x] = V_{\lambda }^{M_n(x)}$
, so
 $V_{\lambda }^{M_n(\mathbb {V})}[G_x][g] = V_{\lambda }^{M_n(x)[g]}$
and this
$V_{\lambda }^{M_n(\mathbb {V})}[G_x][g] = V_{\lambda }^{M_n(x)[g]}$
and this
![]() $\mathcal {P}$
-construction is well-defined. Moreover, the following argument shows that the construction never projects across
$\mathcal {P}$
-construction is well-defined. Moreover, the following argument shows that the construction never projects across
![]() $\lambda $
.
$\lambda $
.
Assume toward a contradiction that there is a level
![]() $\mathcal {P}$
of the
$\mathcal {P}$
of the
![]() $\mathcal {P}$
-construction above
$\mathcal {P}$
-construction above
![]() $M_n(\mathbb {V})|\lambda $
inside
$M_n(\mathbb {V})|\lambda $
inside
![]() $M_n(x)[g]$
such that
$M_n(x)[g]$
such that
![]() $\rho _{\omega }(\mathcal {P}) = \rho < \lambda $
. That means there is an
$\rho _{\omega }(\mathcal {P}) = \rho < \lambda $
. That means there is an
![]() $r\Sigma _{k+1}(\mathcal {P})$
-definable set
$r\Sigma _{k+1}(\mathcal {P})$
-definable set
![]() $a \subseteq \rho $
for some
$a \subseteq \rho $
for some
![]() $k < \omega $
such that
$k < \omega $
such that
![]() $a \notin \mathcal {P}$
. As by the proof of Claim 4,
$a \notin \mathcal {P}$
. As by the proof of Claim 4,
 $M_n(\mathbb {V})|\lambda \in \operatorname {HOD}^{M_n(x)[g]} $
it follows by definability of the
$M_n(\mathbb {V})|\lambda \in \operatorname {HOD}^{M_n(x)[g]} $
it follows by definability of the
![]() $\mathcal {P}$
-construction and of the extender sequence of
$\mathcal {P}$
-construction and of the extender sequence of
 $M_n(V_{\lambda }^{M_n(x)[g]})$
(see Lemma 1.1 in [Reference Schindler14] due to J. Steel) that
$M_n(V_{\lambda }^{M_n(x)[g]})$
(see Lemma 1.1 in [Reference Schindler14] due to J. Steel) that
![]() $\mathcal {P} \in \operatorname {HOD}^{M_n(x)[g]} $
. This means that in particular
$\mathcal {P} \in \operatorname {HOD}^{M_n(x)[g]} $
. This means that in particular
![]() $a \in \operatorname {HOD}^{M_n(x)[g]} $
. But
$a \in \operatorname {HOD}^{M_n(x)[g]} $
. But
![]() $a \subseteq \rho < \lambda $
and by Claim 5,
$a \subseteq \rho < \lambda $
and by Claim 5,
 $V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} } = V_{\lambda }^{M_n(\mathbb {V})} = V_{\lambda }^{\mathcal {P}}$
, so
$V_{\lambda }^{\operatorname {HOD}^{M_n(x)[g]} } = V_{\lambda }^{M_n(\mathbb {V})} = V_{\lambda }^{\mathcal {P}}$
, so
![]() $a \in \mathcal {P}$
. Contradiction.
$a \in \mathcal {P}$
. Contradiction.
Now it follows by construction (see [Reference Schindler and Steel15]) that
 $$\begin{align*}\mathcal{P}^{M_n(x)[g]}(M_n(\mathbb{V})|\lambda)[G_x][g] = M_n(x)[g].\end{align*}$$
$$\begin{align*}\mathcal{P}^{M_n(x)[g]}(M_n(\mathbb{V})|\lambda)[G_x][g] = M_n(x)[g].\end{align*}$$
But this yields that
 $\mathcal {P}^{M_n(x)[g]}(M_n(\mathbb {V})|\lambda )[G_x] = M_n(x)$
, without adding the generic g, by an argument as the one at the end of the previous claim. Moreover,
$\mathcal {P}^{M_n(x)[g]}(M_n(\mathbb {V})|\lambda )[G_x] = M_n(x)$
, without adding the generic g, by an argument as the one at the end of the previous claim. Moreover,
 $\mathcal {P}^{M_n(x)[g]}(M_n(\mathbb {V})|\lambda ) = M_n(\mathbb {V})$
and thus
$\mathcal {P}^{M_n(x)[g]}(M_n(\mathbb {V})|\lambda ) = M_n(\mathbb {V})$
and thus
![]() $M_n(\mathbb {V})[G_x] = M_n(x)$
, as desired.⊣
$M_n(\mathbb {V})[G_x] = M_n(x)$
, as desired.⊣
This argument also shows the following claim.
Claim 7.
 $M_n(\mathbb {V}) \subseteq \operatorname {HOD} ^{M_n(x)[g]}$
.
$M_n(\mathbb {V}) \subseteq \operatorname {HOD} ^{M_n(x)[g]}$
.
Now, the next claim follows from the first half of the proof of Claim 5.
Claim 8.
 $M_n(\mathbb {V})[G_x] = \operatorname {HOD} ^{M_n(x)[g]}[G_x]$
.
$M_n(\mathbb {V})[G_x] = \operatorname {HOD} ^{M_n(x)[g]}[G_x]$
.
Finally, the statement of Claim 8 also holds true without adding the generic
![]() $G_x$
by the argument at the end of the proof of Claim 5. Hence
$G_x$
by the argument at the end of the proof of Claim 5. Hence
 $M_n(\mathbb {V}) = \operatorname {HOD} ^{M_n(x)[g]}$
, as desired.⊣
$M_n(\mathbb {V}) = \operatorname {HOD} ^{M_n(x)[g]}$
, as desired.⊣
Corollary 5.2. Let
![]() $F(s) = s^*$
for
$F(s) = s^*$
for
![]() $s \in [\operatorname {Ord} ]^{<\omega }$
. Then
$s \in [\operatorname {Ord} ]^{<\omega }$
. Then
 $$\begin{align*}\operatorname{HOD}^{M_n(x)[g]} = M_n(\mathcal{M}_{\infty}|\delta_{\infty}, F \upharpoonright \delta_{\infty}). \end{align*}$$
$$\begin{align*}\operatorname{HOD}^{M_n(x)[g]} = M_n(\mathcal{M}_{\infty}|\delta_{\infty}, F \upharpoonright \delta_{\infty}). \end{align*}$$
Proof. Note that
![]() $\mathcal {M}_{\infty }|\delta _{\infty }$
and
$\mathcal {M}_{\infty }|\delta _{\infty }$
and
![]() $F \upharpoonright \delta _{\infty }$
are elements of
$F \upharpoonright \delta _{\infty }$
are elements of
![]() $\operatorname {HOD}^{M_n(x)[g]} $
by construction. Let
$\operatorname {HOD}^{M_n(x)[g]} $
by construction. Let
![]() $\eta = \sup F \, " \delta _{\infty }$
and let
$\eta = \sup F \, " \delta _{\infty }$
and let
![]() $\gamma $
be the least inaccessible cardinal of
$\gamma $
be the least inaccessible cardinal of
![]() $M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
above
$M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
above
![]() $\eta $
. Let
$\eta $
. Let
 $A \subseteq \omega _2^{M_n(x)[g]}$
be as in the statement of Lemma 5.1, i.e., such that
$A \subseteq \omega _2^{M_n(x)[g]}$
be as in the statement of Lemma 5.1, i.e., such that
 $\operatorname {HOD}^{M_n(x)[g]} = M_n(A)$
. Moreover, let
$\operatorname {HOD}^{M_n(x)[g]} = M_n(A)$
. Moreover, let
![]() $\varphi $
be a formula defining A, i.e.,
$\varphi $
be a formula defining A, i.e.,
![]() $\xi \in A$
iff
$\xi \in A$
iff
![]() $M_n(x)[g] \vDash \varphi (\xi )$
. Then, as
$M_n(x)[g] \vDash \varphi (\xi )$
. Then, as
![]() $F(\xi ) = \pi _{\infty }(\xi )$
for
$F(\xi ) = \pi _{\infty }(\xi )$
for
![]() $\xi < \delta _{\infty }$
by Lemma 4.2,
$\xi < \delta _{\infty }$
by Lemma 4.2,

for
![]() $\mathbb {P} = \operatorname {Col} (\omega , {<}\kappa _{\infty })$
. Consider
$\mathbb {P} = \operatorname {Col} (\omega , {<}\kappa _{\infty })$
. Consider
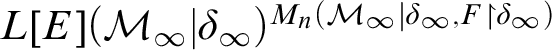 $L[E](\mathcal {M}_{\infty } | \delta _{\infty })^{M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })}$
, the result of a fully backgrounded extender construction in the sense of [Reference Mitchell and Steel7] inside
$L[E](\mathcal {M}_{\infty } | \delta _{\infty })^{M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })}$
, the result of a fully backgrounded extender construction in the sense of [Reference Mitchell and Steel7] inside
![]() $M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
above
$M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
above
![]() $\mathcal {M}_{\infty } | \delta _{\infty }$
. The premice
$\mathcal {M}_{\infty } | \delta _{\infty }$
. The premice
![]() $M_n(\mathcal {M}_{\infty } | \delta _{\infty })$
and
$M_n(\mathcal {M}_{\infty } | \delta _{\infty })$
and
 $L[E](\mathcal {M}_{\infty } | \delta _{\infty })^{M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })}$
successfully compare to a common proper class premouse without drops on the main branches. Since the iterations take place above
$L[E](\mathcal {M}_{\infty } | \delta _{\infty })^{M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })}$
successfully compare to a common proper class premouse without drops on the main branches. Since the iterations take place above
![]() $\delta _{\infty }$
,
$\delta _{\infty }$
,
![]() $\xi < \delta _{\infty }$
is not moved and we have by elementarity
$\xi < \delta _{\infty }$
is not moved and we have by elementarity

Therefore it follows that
![]() $A \in M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
.
$A \in M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
.
By the same argument as in the proof of Claim 3 in the proof of Lemma 5.1 we now obtain that
![]() $\gamma $
is also the least inaccessible cardinal above
$\gamma $
is also the least inaccessible cardinal above
![]() $\eta $
of
$\eta $
of
![]() $M_n(A)$
and the universes of
$M_n(A)$
and the universes of
![]() $M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
and
$M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
and
![]() $M_n(A)$
agree up to
$M_n(A)$
agree up to
![]() $\gamma $
. In particular, we can rearrange
$\gamma $
. In particular, we can rearrange
![]() $M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
and
$M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })$
and
![]() $M_n(A)$
as
$M_n(A)$
as
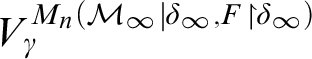 $V_{\gamma }^{M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })}$
-premice. As such it follows that the following equalities for classes (not structures) hold:
$V_{\gamma }^{M_n(\mathcal {M}_{\infty }|\delta _{\infty }, F \upharpoonright \delta _{\infty })}$
-premice. As such it follows that the following equalities for classes (not structures) hold:
 $$ \begin{align*} M_n(\mathcal{M}_{\infty}|\delta_{\infty}, F \upharpoonright \delta_{\infty}) & = M_n(V_{\gamma}^{M_n(\mathcal{M}_{\infty}|\delta_{\infty}, F \upharpoonright \delta)}) \\ & = M_n(A) = \operatorname{HOD}^{M_n(x)[g]}.\\[-2.8pc] \end{align*} $$
$$ \begin{align*} M_n(\mathcal{M}_{\infty}|\delta_{\infty}, F \upharpoonright \delta_{\infty}) & = M_n(V_{\gamma}^{M_n(\mathcal{M}_{\infty}|\delta_{\infty}, F \upharpoonright \delta)}) \\ & = M_n(A) = \operatorname{HOD}^{M_n(x)[g]}.\\[-2.8pc] \end{align*} $$
⊣
The following corollary follows immediately from Lemma 4.2 and Corollary 5.2.
Corollary 5.3.
 $\operatorname {HOD}^{M_n(x)[g]} = M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty })$
.
$\operatorname {HOD}^{M_n(x)[g]} = M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty })$
.
We now consider the iteration strategy for
![]() $\mathcal {M}_{\infty }$
. Let
$\mathcal {M}_{\infty }$
. Let
![]() $\Lambda $
be the restriction of
$\Lambda $
be the restriction of
 $\Sigma _{M_{n+1}^{-}}$
to correctly guided finite stacks
$\Sigma _{M_{n+1}^{-}}$
to correctly guided finite stacks
![]() $\vec {\mathcal {T}}$
on
$\vec {\mathcal {T}}$
on
![]() $\mathcal {M}_{\infty }|\delta _{\infty }$
such that
$\mathcal {M}_{\infty }|\delta _{\infty }$
such that
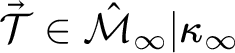 $\vec {\mathcal {T}} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
, where
$\vec {\mathcal {T}} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
, where
![]() $\kappa _{\infty }$
is the least inaccessible cardinal in
$\kappa _{\infty }$
is the least inaccessible cardinal in
![]() $\hat {\mathcal {M}}_{\infty }$
above
$\hat {\mathcal {M}}_{\infty }$
above
![]() $\delta _{\infty }$
.
$\delta _{\infty }$
.
Lemma 5.4.
![]() $\Lambda \in \operatorname {HOD}^{M_n(x)[g]} $
.
$\Lambda \in \operatorname {HOD}^{M_n(x)[g]} $
.
Proof. Let
![]() $\mathcal {T}$
be a maximal tree on
$\mathcal {T}$
be a maximal tree on
![]() $\mathcal {M}_{\infty } | \delta _{\infty }$
with
$\mathcal {M}_{\infty } | \delta _{\infty }$
with
 $\mathcal {T} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
. Moreover, let
$\mathcal {T} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
. Moreover, let
![]() $b = \Lambda (\mathcal {T})$
. Let
$b = \Lambda (\mathcal {T})$
. Let
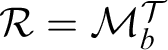 $\mathcal {R} = \mathcal {M}_b^{\mathcal {T}}$
be the last model of
$\mathcal {R} = \mathcal {M}_b^{\mathcal {T}}$
be the last model of
![]() $\mathcal {T}^\smallfrown b$
. Then
$\mathcal {T}^\smallfrown b$
. Then
![]() $\mathcal {R} \in \operatorname {HOD}^{M_n(x)[g]} $
. Moreover, let
$\mathcal {R} \in \operatorname {HOD}^{M_n(x)[g]} $
. Moreover, let
 $\delta _{\infty }^{\mathcal {F}^*}$
be the least Woodin cardinal in
$\delta _{\infty }^{\mathcal {F}^*}$
be the least Woodin cardinal in
 $\mathcal {M}_{\infty }^{\mathcal {F}^*}$
, the direct limit of the system
$\mathcal {M}_{\infty }^{\mathcal {F}^*}$
, the direct limit of the system
![]() $\mathcal {F}^{*,M(y)}$
for some/all dlm-suitable
$\mathcal {F}^{*,M(y)}$
for some/all dlm-suitable
![]() $M(y)$
in
$M(y)$
in
![]() $\hat {\mathcal {M}}_{\infty }[H]$
. Then
$\hat {\mathcal {M}}_{\infty }[H]$
. Then
 $\mathcal {M}_{\infty }^{\mathcal {F}^*} | \delta _{\infty }^{\mathcal {F}^*}$
is an iterate of
$\mathcal {M}_{\infty }^{\mathcal {F}^*} | \delta _{\infty }^{\mathcal {F}^*}$
is an iterate of
![]() $\mathcal {R}$
. As
$\mathcal {R}$
. As
 $\pi _{\infty } \upharpoonright \delta _{\infty } \in \operatorname {HOD}^{M_n(x)[g]} $
, we can identify b inside
$\pi _{\infty } \upharpoonright \delta _{\infty } \in \operatorname {HOD}^{M_n(x)[g]} $
, we can identify b inside
![]() $M_n(x)[g]$
as the unique branch through
$M_n(x)[g]$
as the unique branch through
![]() $\mathcal {T}$
which is
$\mathcal {T}$
which is
![]() $(\pi _{\infty } \upharpoonright \delta _{\infty })$
-realizable, i.e., such that there is an elementary embedding
$(\pi _{\infty } \upharpoonright \delta _{\infty })$
-realizable, i.e., such that there is an elementary embedding
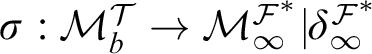 $\sigma : \mathcal {M}_b^{\mathcal {T}} \rightarrow \mathcal {M}_{\infty }^{\mathcal {F}^*} | \delta _{\infty }^{\mathcal {F}^*}$
with
$\sigma : \mathcal {M}_b^{\mathcal {T}} \rightarrow \mathcal {M}_{\infty }^{\mathcal {F}^*} | \delta _{\infty }^{\mathcal {F}^*}$
with
 $\pi _{\infty } \upharpoonright \delta _{\infty } = \sigma \circ i_b^{\mathcal {T}}$
.
$\pi _{\infty } \upharpoonright \delta _{\infty } = \sigma \circ i_b^{\mathcal {T}}$
.
The same argument applies to pseudo-normal iterates
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {M}_{\infty }$
with
$\mathcal {M}_{\infty }$
with
 $\mathcal {N}|\delta ^{\mathcal {N}} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
and maximal iteration trees
$\mathcal {N}|\delta ^{\mathcal {N}} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
and maximal iteration trees
![]() $\mathcal {T}$
on
$\mathcal {T}$
on
![]() $\mathcal {N} | \delta ^{\mathcal {N}}$
such that
$\mathcal {N} | \delta ^{\mathcal {N}}$
such that
 $\mathcal {T} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
, hence
$\mathcal {T} \in \hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
, hence
![]() $\Lambda \in \operatorname {HOD}^{M_n(x)[g]} $
.⊣
$\Lambda \in \operatorname {HOD}^{M_n(x)[g]} $
.⊣
Similarly to Lemma 3.47 in [Reference Steel, Woodin, Kechris, Löwe and Steel23] we finally need a method of Boolean-valued comparison. As the proof is analogous we omit it.
Lemma 5.5. Let H be
![]() $\operatorname {Col} (\omega , {<}\kappa _{\infty })$
-generic over
$\operatorname {Col} (\omega , {<}\kappa _{\infty })$
-generic over
![]() $\hat {\mathcal {M}}_{\infty }$
, and let
$\hat {\mathcal {M}}_{\infty }$
, and let
![]() $\mathcal {Q}$
be such that
$\mathcal {Q}$
be such that
![]() Then there is an
Then there is an
![]() $\mathcal {R}$
such that
$\mathcal {R}$
such that
-
(1)
 $\mathcal {R}$
is a pseudo-normal iterate of
$\mathcal {R}$
is a pseudo-normal iterate of
 $\mathcal {Q}$
,
$\mathcal {Q}$
, -
(2)
 $\mathcal {R}$
is a
$\mathcal {R}$
is a
 $\Sigma _{M_{n+1}^-}$
-iterate of
$\Sigma _{M_{n+1}^-}$
-iterate of
 $\mathcal {M}_{\infty }$
, and
$\mathcal {M}_{\infty }$
, and -
(3)
 $\mathcal {R} \in \hat {\mathcal {M}}_{\infty }$
.
$\mathcal {R} \in \hat {\mathcal {M}}_{\infty }$
.
Finally, we can finish the proof of Theorem 1.1.
Theorem 5.6.
 $$\begin{align*}\operatorname{HOD}^{M_n(x)[g]} = M_n(\mathcal{M}_{\infty}|\delta_{\infty}, \pi_{\infty} \upharpoonright \delta_{\infty}) = M_n(\hat{\mathcal{M}}_{\infty}|\kappa_{\infty}, \Lambda).\end{align*}$$
$$\begin{align*}\operatorname{HOD}^{M_n(x)[g]} = M_n(\mathcal{M}_{\infty}|\delta_{\infty}, \pi_{\infty} \upharpoonright \delta_{\infty}) = M_n(\hat{\mathcal{M}}_{\infty}|\kappa_{\infty}, \Lambda).\end{align*}$$
Proof.
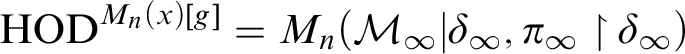 $\operatorname {HOD}^{M_n(x)[g]} = M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty })$
is Corollary 5.3. Moreover,
$\operatorname {HOD}^{M_n(x)[g]} = M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty })$
is Corollary 5.3. Moreover,
 $M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty }) = M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
follows from Lemma 5.5 as follows. First,
$M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty }) = M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
follows from Lemma 5.5 as follows. First,
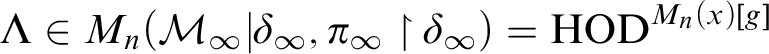 $\Lambda \in M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty }) = \operatorname {HOD}^{M_n(x)[g]} $
and
$\Lambda \in M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty }) = \operatorname {HOD}^{M_n(x)[g]} $
and
 $\hat {\mathcal {M}}_{\infty }|\kappa _{\infty } \in M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty })$
by considering the
$\hat {\mathcal {M}}_{\infty }|\kappa _{\infty } \in M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty })$
by considering the
![]() $Lp^n$
-stack on
$Lp^n$
-stack on
![]() $\mathcal {M}_{\infty }|\delta _{\infty }$
. The direct limit of
$\mathcal {M}_{\infty }|\delta _{\infty }$
. The direct limit of
![]() $\mathcal {F}^{*,M(y)}$
for some
$\mathcal {F}^{*,M(y)}$
for some
![]() $M(y)$
is the same as the direct limit of all
$M(y)$
is the same as the direct limit of all
![]() $\Lambda $
-iterates of
$\Lambda $
-iterates of
![]() $\mathcal {M}_{\infty }$
which are an element of
$\mathcal {M}_{\infty }$
which are an element of
 $\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
via the comparison maps. Moreover, we have that
$\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }$
via the comparison maps. Moreover, we have that
![]() $\pi _{\infty }$
is the canonical direct limit map of this system and therefore definable from
$\pi _{\infty }$
is the canonical direct limit map of this system and therefore definable from
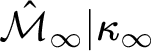 $\hat {\mathcal {M}}_{\infty } | \kappa _{\infty }$
and
$\hat {\mathcal {M}}_{\infty } | \kappa _{\infty }$
and
![]() $\Lambda $
. So
$\Lambda $
. So
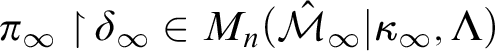 $\pi _{\infty } \upharpoonright \delta _{\infty } \in M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
. Now,
$\pi _{\infty } \upharpoonright \delta _{\infty } \in M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
. Now,
 $M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty }) = M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
follows analogous to the proof of Corollary 5.2.⊣
$M_n(\mathcal {M}_{\infty }|\delta _{\infty }, \pi _{\infty } \upharpoonright \delta _{\infty }) = M_n(\hat {\mathcal {M}}_{\infty }|\kappa _{\infty }, \Lambda )$
follows analogous to the proof of Corollary 5.2.⊣
Note that Theorem 4.3 and Lemma 5.1 together imply Corollary 1.2, i.e., that the
![]() $\operatorname {GCH} $
holds in
$\operatorname {GCH} $
holds in
![]() $\operatorname {HOD}^{M_n(x)[g]} $
. Finally, most of the arguments we gave in this and the previous sections generalize with only small changes to more arbitrary canonical self-iterable inner models, e.g.,
$\operatorname {HOD}^{M_n(x)[g]} $
. Finally, most of the arguments we gave in this and the previous sections generalize with only small changes to more arbitrary canonical self-iterable inner models, e.g.,
![]() $M_{\omega }$
,
$M_{\omega }$
,
![]() $M_{\omega +42}$
. We leave the details to the reader.
$M_{\omega +42}$
. We leave the details to the reader.
Acknowledgments
The authors thank Farmer Schlutzenberg for the helpful discussions during the 4th Münster conference on inner model theory in the summer of 2017. Finally, the authors thank the referee for carefully reading the paper and making several helpful comments and suggestions.
Part of this work was done whilst the authors were visiting fellows at the Isaac Newton Institute for Mathematical Sciences in the programme Mathematical, Foundational and Computational Aspects of the Higher Infinite (HIF) funded by EPSRC grant EP/K032208/1. The first author, formerly known as Sandra Uhlenbrock, was partially supported by FWF grant number P 28157 and in addition gratefully acknowledges funding from L’ORÉAL Austria, in collaboration with the Austrian UNESCO Commission and in cooperation with the Austrian Academy of Sciences—Fellowship Determinacy and Large Cardinals. The second author was partially supported by the NSF Career Award DMS-1352034.