Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T08:07:49.737Z Has data issue: false hasContentIssue false
  • English
  • Français

On the weak Kleene scheme in Kripke's theory of truth

Published online by Cambridge University Press:  12 March 2014

James Cain  and
Zlatan Damnjanovic
James Cain
Affiliation:
Department of Philosophy, University of Cincinnati, Cincinnati, Ohio 45221
Zlatan Damnjanovic
Affiliation:
School of Philosophy, University of Southern California, Los Angeles, California 90089
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that the following features hold of AR + T under the strong Kleene scheme, regardless of the way the language is Gödel numbered:

1. There exist sentences that are neither paradoxical nor grounded.

2. There are 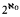fixed points.

3. In the minimal fixed point the weakly definable sets (i.e., sets definable as {n ∣ A(n) is true in the minimal fixed point}, where A(x) is a formula of AR + T) are precisely the 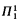sets.

4. In the minimal fixed point the totally defined sets (sets weakly defined by formulae all of whose instances are true or false) are precisely the 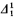sets.

5. The closure ordinal for Kripke's construction of the minimal fixed point is .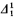

In contrast, we show that under the weak Kleene scheme, depending on the way the Gödel numbering is chosen:

1. There may or may not exist nonparadoxical, ungrounded sentences.

2. The number of fixed points may be any positive finite number, ℵ0, or .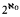

3. In the minimal fixed point, the sets that are weakly definable may range from a subclass of the sets 1-1 reducible to the truth set of AR to the 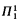sets, including intermediate cases.

4. Similarly, the totally definable sets in the minimal fixed point range from precisely the arithmetical sets up to precisely the 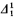sets.

5. The closure ordinal for the construction of the minimal fixed point may be ω, 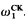, or any successor limit ordinal in between.

In addition we suggest how one may supplement AR + T with a function symbol interpreted by a certain primitive recursive function so that, irrespective of the choice of the Gödel numbering, the resulting language based on the weak Kleene scheme has the five features noted above for the strong Kleene language.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 4 , December 1991 , pp. 1452 - 1468
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Burgess, J. P., The truth is never simple, this Journal, vol. 51 (1986), pp. 663–681.Google Scholar
[2]Fitting, M., Notes on the mathematical aspects of Kripke's theory of truth, Notre Dame Journal of Formal Logic, vol. 27 (1986), pp. 75–88.CrossRefGoogle Scholar
[3]Kleene, S. C., Introduction to metamathematics, Van Nostrand, New York, 1952.Google Scholar
[4]Kripke, S., Outline of a theory of truth, Journal of Philosophy, vol. 72 (1975), pp. 690–716; reprinted in Recent essays on truth and the liar paradox (R. L. Martin, editor), Oxford University Press, New York, 1984, pp. 53–81.CrossRefGoogle Scholar
[5]Rogers, H., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar