Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-20T05:22:36.337Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of the Medvedev lattice

Published online by Cambridge University Press:  12 March 2014

Sebastiaan A. Terwijn
Sebastiaan A. Terwijn*
Affiliation:
Kurt Gödel Research Center For Mathematical Logic, University of Vienna, Währinger Straβe 25, 1040 Vienna, Austria, E-mail: terwijn@logic.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the structure of the Medvedev lattice as a partial order. We prove that every interval in the lattice is either finite, in which case it is isomorphic to a finite Boolean algebra, or contains an antichain of size 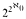. the size of the lattice itself. We also prove that it is consistent with ZFC that the lattice has chains of size 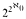. and in fact that these big chains occur in every infinite interval. We also study embeddings of lattices and algebras. We show that large Boolean algebras can be embedded into the Medvedev lattice as upper semilattices, but that a Boolean algebra can be embedded as a lattice only if it is countable. Finally we discuss which of these results hold for the closely related Muchnik lattice.

Keywords

Medvedev degreeschainsantichainslattice embeddings
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 2 , June 2008 , pp. 543 - 558
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Binns, Stephen and Simpson, Stephen G., Embeddings into the Medvedev and Muchnik lattices of classes, Archive for Mathematical Logic, vol. 43 (2004), pp. 399–414.CrossRefGoogle Scholar
[2]Dyment, Elena Z., Certain properties of the Medvedev lattice, Mathematics of the USSR Sbornik, vol. 30 (1976), pp. 321–340, English translation.CrossRefGoogle Scholar
[3]Kunen, Kenneth, Set theory: An introduction to independence proofs, North-Holland, 1983.Google Scholar
[4]Medvedev, Yuri T., Degrees of difficulty of the mass problems, Doklady Akademii Nauk SSSR, vol. 104 (1955), no. 4, pp. 501–504.Google Scholar
[5]Muchnik, Albert A., Negative answer to the problem of reducibility in the theory of algorithms, Doklady Akademii Nauk SSSR (N.S.), vol. 108 (1956), pp. 194–197.Google Scholar
[6]Muchnik, Albert A., On strong and weak reducibility of algorithmic problems, Sibirskii Mathematicheskii Zhurnal. vol. 4 (1963). pp. 1328–1341, in Russian.Google Scholar
[7]Odifreddi, Piergiorgio G., Classical recursion theory, I, Studies in logic and the foundations of mathematics, vol. 125, North-Holland, 1989.Google Scholar
[8]Odifreddi, Piergiorgio G., Classical recursion theory, II, Studies in logic and the foundations of mathematics, vol. 143, North-Holland, 1999.Google Scholar
[9]Platek, Richard A., A note on the cardinality of the Medvedev lattice. Proceedings of the American Mathematical Society, vol. 25 (1970), p. 917.Google Scholar
[10]Rogers, Hartley Jr., Theory of recursive functions and effective computability, McGraw-Hill, 1967.Google Scholar
[11]Sacks, Gerald E., On suborderings of degrees of recursive unsolvability, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 7 (1961), pp. 46–56.CrossRefGoogle Scholar
[12]Simpson, Stephen, Mass problems and randomness, The Bulletin of Symbolic Logic, vol. 11 (2005), no. 1, pp. 1–27.CrossRefGoogle Scholar
[13]Sorbi, Andrea, Some remarks on the algebraic structure of the Medvedev lattice, this Journal, vol. 55 (1990), no. 2, pp. 831–853.Google Scholar
[14]Sorbi, Andrea, The Medvedev lattice of degrees of difficulty, Computability, enumerability, unsolvability: Directions in recursion theory (Cooper, S. B., Slaman, T. A., and Wainer, S. S., editors), London Mathematical Society Lecture Notes, vol. 224, Cambridge University Press, 1996, pp. 289–312.CrossRefGoogle Scholar
[15]Sorbi, Andrea and Terwijn, Sebastiaan A., Intermediate logics and factors of the Medvedev lattice, to appear in Annals of Pure and Applied Logic.Google Scholar
[16]Terwijn, Sebastiaan A., The finite intervals of the Muchnik lattice, posted on arXiv, 06 28, 2006.Google Scholar