Let T be a theory in a first-order language L. Let L have a predicate ν0 ≺ ν1 such that in every model 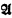of T, the interpretation 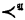of ≺ is a linear ordering with infinite field. The order-type of this ordering will be called the order-type of the model .

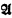Several recent theorems have the following form: if T has a model of order-type ξ then T has a model of order-type ζ (see [1]). We shall add one to the list. The new feature of our result is that the order-type ζ may be in a sense “opposite” to ξ. Silver's Theorem 2.24 of [3] is a corollary of Theorem 1 below.

Theorem 1. Let κ be a strong limit number (i.e. μ < κ implies 2μ < κ). Suppose λ < κ, and suppose that for every cardinal μ < κ, T has a model 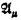with 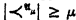where the order-type of 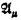contains no descending well-ordered sequences of length λ. Then for every cardinal μ ≥ the cardinality ∣L∣ of the language L, T has models 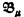and 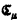such that

(a) the field of 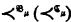is the union of ≤ ∣L∣ well-ordered (inversely well-ordered) parts;

(b) .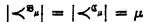

The proof is by Ehrenfeucht-Mostowski models; we presuppose [2].