Let S be a recursive theory. Let a theory T* consisting of Σ1 sentences be called maximal (with respect to S) if T* is maximal consistent with S, i.e. there is no Σ1 sentence consistent with T* + S which is not in T*.

A maximal theory with respect to IΔ0 was considered by Wilkie and Paris in [WP] in connection with the end-extension problem.

Let us recall that IΔ0 is the fragment of Peano arithmetic consisting of the finite collection of algebraic axioms PA− together with the induction scheme restricted to bounded formulas.

The main open problem concerning the end-extendability of models of IΔ0 is the following:

(*) Does every model of IΔ0 + BΣ1 have a proper end-extension to a model of IΔ0?

Here BΣ1 is the following collection scheme:

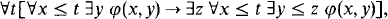
where φ runs over bounded formulas and may contain parameters.

It is well known(see [KP]) that if I is a proper initial segment of a model M of IΔ0, then I satisfies IΔ0 + BΣ1.

For a wide discussion of the problem (*) see [WP]. Wilkie and Paris construct in [WP] a model M of IΔ0 + BΣ1 which has no proper end-extension to a model of IΔ0 under the assumption IΔ0 ⊢¬Δ0 H (see [WP] for an explanation of this assumption). Their model M is a model of a maximal theory T* where S = IΔ0.

Moreover, T*, which is the set Σ1(M) of all Σ1 sentences true in M, is not codable in M.