No CrossRef data available.
Article contents
On external Scott algebras in nonstandard models of Peano arithmetic
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove that a necessary and sufficient condition for a countable set 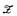 of sets of integers to be equal to the algebra of all sets of integers definable in a nonstandard elementary extension of ω by a formula of the PA language which may include the standardness predicate but does not contain nonstandard parameters, is as follows:
of sets of integers to be equal to the algebra of all sets of integers definable in a nonstandard elementary extension of ω by a formula of the PA language which may include the standardness predicate but does not contain nonstandard parameters, is as follows: 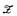 is closed under arithmetical definability and contains 0(ω) the set of all (Gödel numbers of) true arithmetical sentences.
is closed under arithmetical definability and contains 0(ω) the set of all (Gödel numbers of) true arithmetical sentences.
Some results related to definability of sets of integers in elementary extensions of ω are included.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996




