Article contents
ON EXTENSIONS OF PARTIAL ISOMORPHISMS
Published online by Cambridge University Press: 20 July 2020
Abstract
In this paper we study a notion of HL-extension (HL standing for Herwig–Lascar) for a structure in a finite relational language
$\mathcal {L}$
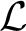 . We give a description of all finite minimal HL-extensions of a given finite
$\mathcal {L}$
. We give a description of all finite minimal HL-extensions of a given finite
$\mathcal {L}$
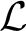 -structure. In addition, we study a group-theoretic property considered by Herwig–Lascar and show that it is closed under taking free products. We also introduce notions of coherent extensions and ultraextensive
$\mathcal {L}$
-structure. In addition, we study a group-theoretic property considered by Herwig–Lascar and show that it is closed under taking free products. We also introduce notions of coherent extensions and ultraextensive
$\mathcal {L}$
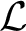 -structures and show that every countable
$\mathcal {L}$
-structures and show that every countable
$\mathcal {L}$
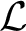 -structure can be extended to a countable ultraextensive structure. Finally, it follows from our results that the automorphism group of any countable ultraextensive
$\mathcal {L}$
-structure can be extended to a countable ultraextensive structure. Finally, it follows from our results that the automorphism group of any countable ultraextensive
$\mathcal {L}$
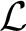 -structure has a dense locally finite subgroup.
-structure has a dense locally finite subgroup.
Keywords
- Type
- Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 2
- Cited by





