Article contents
On decidable varieties of Heyting algebras
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we present a new proof of a decidability result for the firstorder theories of certain subvarieties of Heyting algebras. By a famous result of Grzegorczyk, the full first-order theory of Heyting algebras is undecidable. In contrast, the first-order theory of Boolean algebras and of many interesting subvarieties of Boolean algebras is decidable by a result of Tarski [8]. In fact, Kozen [6] gives a comprehensive quantitative classification of the complexities of the first-order theories of various subclasses of Boolean algebras (including the full variety).
This stark contrast may be reconciled from the standpoint of universal algebra as arising out of the byplay between structure and decidability: A good structure theory entails positive decidability results. Boolean algebras have a well-developed structure theory [5], while the corresponding theory for Heyting algebras is quite meagre. Viewed in this way, we may hope to obtain decidability results if we focus attention on subclasses of Heyting algebras with good structural properties.
K. Idziak and P. M. Idziak [4] have considered an interesting subvariety of Heyting algebras, 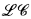 , which is the variety generated by all linearly-ordered Heyting algebras. This variety is shown to be the largest subvariety of Heyting algebras with a decidable theory of its finite members. However their proof is rather indirect, proceeding via semantic interpretation into the monadic second order theory of trees. The latter is a powerful theory—it interprets many other theories—but is computationally highly infeasible. In fact, by a celebrated theorem of Rabin, its complexity is not bounded by any elementary recursive function. Consequently, the proof of [4], besides being indirect, also gives no information on the quantitative computational complexity of the theory of
, which is the variety generated by all linearly-ordered Heyting algebras. This variety is shown to be the largest subvariety of Heyting algebras with a decidable theory of its finite members. However their proof is rather indirect, proceeding via semantic interpretation into the monadic second order theory of trees. The latter is a powerful theory—it interprets many other theories—but is computationally highly infeasible. In fact, by a celebrated theorem of Rabin, its complexity is not bounded by any elementary recursive function. Consequently, the proof of [4], besides being indirect, also gives no information on the quantitative computational complexity of the theory of 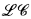 .
.
Here we pursue the theme of structure and decidability. We isolate the indecomposable algebras in 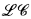 and use this to prove a theorem on the structure of if
and use this to prove a theorem on the structure of if 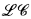 -algebras. This theorem relates the
-algebras. This theorem relates the 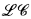 -algebras structurally to Boolean algebras. This enables us to bootstrap the known decidability results for Boolean algebras to the variety if
-algebras structurally to Boolean algebras. This enables us to bootstrap the known decidability results for Boolean algebras to the variety if 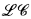 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 5
- Cited by




