Let T extend the theory P of Peano arithmetic, and suppose 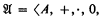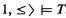. Form from 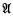a model , in analogy to the way in which the ordered ring of integers is formed from the standard model of arithmetic. Let P′ and T′ be the corresponding analogues of P and T respectively. Now consider the group 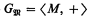. In [5] MacDowell and Specker set out to determine the structure of such groups. (The precise statement in [5] refers to the ring of integers rather than the ordered ring. However, as pointed out to us by J. Knight, since Lagrange's Theorem that a positive integer is the sum of four squares is provable in the analogue of P′ for rings (see, for example, the proof in [7, p. 102]), the set of positive elements is definable in the ring, and consequently, so is the ordering. Thus, for the present purpose it makes no difference which of the two structures is used. Of course, one needs the ordering to discuss end extensions, as considered in [5]. On the other hand, one should be aware that in Pr′ one cannot define an ordering, where the theory Pr′ is the theory of the group of integers with distinguished element 1, 〈Z, +, 1〉. The constant 1 is needed so that divisibility mod n can be expressed. We will return to this point later.) In §1 we shall outline the results in this direction obtained in [5].

Lipshitz and Nadel, unaware that a similar question had been posed and investigated in [5] (though, of course aware that [5] contained the celebrated results on end extensions) set out to characterize those models 〈A, +〉 of Pr = Presburger Arithmetic (the complete theory of 〈ω, +〉) which can be expanded to models 〈A, +, ·, 0, 1, ≤〉 of P. They were able to give a complete characterization for countable models 〈A, +〉 in [4], which we describe in §2.