Article contents
Namba Forcing and No Good Scale
Published online by Cambridge University Press: 12 March 2014
Abstract
We develop a version of Namba forcing which is useful for constructing models with no good scale on ℵω. A model is produced in which 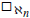 holds for all finite n ≥ 1, but there is no good scale on ℵω; this strengthens a theorem of Cummings, Foreman, and Magidor [3] on the non-compactness of square.
holds for all finite n ≥ 1, but there is no good scale on ℵω; this strengthens a theorem of Cummings, Foreman, and Magidor [3] on the non-compactness of square.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2013
References
REFERENCES
- 1
- Cited by




