Hostname: page-component-68945f75b7-qf55q Total loading time: 0 Render date: 2024-08-06T01:06:10.619Z Has data issue: false hasContentIssue false
  • English
  • Français

More undecidable lattices of Steinitz exchange systems

Published online by Cambridge University Press:  12 March 2014

L. R. Galminas  and
John W. Rosenthal
L. R. Galminas
Affiliation:
Department of Mathematics, Northwestern State University of Louisiana, Natchitoches, LA 71457., USA, E-mail: galminas@nsula.edu
John W. Rosenthal
Affiliation:
Department of Mathematics, Ithaca College, Ithaca. NY 14850, USA, E-mail: rosentha@ithaca.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the first order theory of the lattice 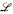<ω(S) of finite dimensional closed subsets of any nontrivial infinite dimensional Steinitz Exhange System S has logical complexity at least that of first order number theory and that the first order theory of the lattice 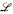(S∞) of computably enumerable closed subsets of any nontrivial infinite dimensional computable Steinitz Exchange System S∞ has logical complexity exactly that of first order number theory. Thus, for example, the lattice of finite dimensional subspaces of a standard copy of ⊕ωQ interprets first order arithmetic and is therefore as complicated as possible. In particular, our results show that the first order theories of the lattice 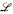(V∞) of c.e. subspaces of a fully effective ℵ0-dimensional vector space V∞ and the lattice of c.e. algebraically closed subfields of a fully effective algebraically closed field F∞ of countably infinite transcendence degree each have logical complexity that of first order number theory.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 2 , June 2002 , pp. 859 - 878
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C. J. and Downey, R., Decidable subspaces and recursively enumerable subspaces, this Journal, vol.49 (1984), pp. 1137–1145.Google Scholar
[2]Ash, C. J. and Rosenthal, J. W., Some theories associated with algebraically closed fields, this Journal, vol. 45 (1980). pp. 359–362.Google Scholar
[3]Ash, C. J., Intersections of algebraically closed fields, Annals of Pure and Applied Logic, vol. 30 (1986), pp. 103–119.CrossRefGoogle Scholar
[4]Baldwin, J. T., Recurison theory and abstract dependence, Pairas Logic Symposium (Metakides, G., editor). North-Holland Studies in Logic. North-Holland, New York, 1982. pp. 67–76.CrossRefGoogle Scholar
[5]Belegradek, O., On algebraically closed groups, Algebra i Logika, vol. 13 (1974). no. 3, pp. 813–816.Google Scholar
[6]Carrol, J. S., The undecidability of the lattice of r.e. subalgebras of a recursive Boolean algebra. Notices of the American Mathematical Society, 83T-03-281.Google Scholar
[7]Dekker, J. C. E., Countable vector spaces with recursive operations, Part I, this Journal, vol. 34 (1969), pp. 1137–1145.Google Scholar
[8]Downly, R. G., Abstract dependence, recursion theory, and the lattice of r.e. filters, Ph.D. thesis, Monash University, 1982.Google Scholar
[9]Downly, R. G., Undecidability of (F ∞) and other lattices of r.e. substructures, Annals of Pure and Applied Logic, vol. 32 (1986). pp. 17–26.CrossRefGoogle Scholar
[10]Downly, R. G., Correction to: Undecidability of (F ∞) and other lattices of r.e. substructures, Annals of Pure and Applied Logic, vol. 48 (1990), pp. 299–301.CrossRefGoogle Scholar
[11]Downly, R. G. and Kalantari, I.Effective extensions of linear forms on a recursive vector space over a recursive field, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 31 (1985), pp. 193–200.CrossRefGoogle Scholar
[12]Downly, R. G., Laforte, G., and Nies, A., Computably enumerable sets and quasi-reducibility, Annals of Pure and Applied Logic, vol. 95 (1998). pp. 1–35.CrossRefGoogle Scholar
[13]Galminas, L. R., Degrees of algorithmic complexity associated with recursively enumerable substructures, Ph.D. thesis. University of Wisconsin, Madison, 1994.Google Scholar
[14]Guichard, D., Automorphisms and large submodels in effective algebra, Ph.D. thesis. University of Wisconsin, Madison, 1982.Google Scholar
[15]Guichard, D., Automorphisms of substructure lattices in recursive algebra, Annals of Pure and Applied Logic, vol. 25 (1983). pp. 47–58.CrossRefGoogle Scholar
[16]Hough, W. V. D. and Pedoe, D., Methods of Algebraic Geometry, vol. 1, Cambridge University Press, 1947.Google Scholar
[17]Kalantari, I., Automorphisms of the lattice of recursively enumerable vector spaces. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 25 (1979), pp. 385–401.CrossRefGoogle Scholar
[18]Lerman, M. and Remmel, J. B., The universal splitting property, I, Logic Colloquium '80, North-Holland Studies in Logic, vol. 108, North-Holland, New York, 1982, pp. 181–209.Google Scholar
[19]Lerman, M., The universal splitting property, II, this Journal, vol. 49 (1984). pp. 137–150.Google Scholar
[20]Macintyre, A., Omitting quantifier free types in generic stuctures, this Journal, vol. 37 (1972), pp. 512–520.Google Scholar
[21]Magidor, M., Rosenthal, J. W., Rubin, M., and Srour, G., Some highly undecidable lattices, Annals of Pure and Applied Logic, vol. 46 (1990), pp. 41–63.CrossRefGoogle Scholar
[22]Metakides, G. and Nerode, A., Recursively enumerable vector spaces, Annals of Mathematical Logic, vol. 11 (1977), pp. 147–171.CrossRefGoogle Scholar
[23]Metakides, G., Recursion theory on fields and abstract dependence, Journal of Algebra, vol. 65 (1980), pp. 36–59.CrossRefGoogle Scholar
[24]Nerode, A. and Remmel, J. B., Recursion theory on matroids, Pairas Logic Symposium (Metakides, G., editor), North-Holland, Amsterdam, 1983, pp. 41–67.Google Scholar
[25]Nerode, A., A survey of lattices of r.e. substructures, Recursion Theory (Nerode, A. and Shore, R., editors), 1985, Proceedings of the Symposium on Pure Mathematics, vol. 42 American Mathematical Society, Providence, pp. 323–375.CrossRefGoogle Scholar
[26]Nerode, A. and Smith, R., The undecidability of the lattice of r.e. subspaces, Proceedings of the Third Brazilian Conference on Mathematical Logic (Arruda, A. I., Costa, N. C. A. Di, and Sette, A. M., editors), 1982, pp. 245–252.Google Scholar
[27]Nies, A., Intervals of the lattice of computably enumertable sets and effective Boolean algebras, Bulletin of the London Mathematical Society, vol. 29 (1997), pp. 683–692.CrossRefGoogle Scholar
[28]Remmel, J. B., Recursively enumerable Boolean algebras, Annals of Mathematical Logic, vol. 14 (1978), pp. 75–107.CrossRefGoogle Scholar
[29]Remmel, J. B., Complementation in the lattice of subalgebras of a Boolean algebra, Algebra Universalis, vol. 10 (1980). pp. 48–64.CrossRefGoogle Scholar
[30]Remmel, J. B., Recursion theory on algebraic structures with an independent set, Annals of Mathematical Logic, vol. 18 (1980), pp. 153–191.CrossRefGoogle Scholar
[31]Shelah, S., Interpreting set theory in the endomorphism semi-group of a free algebra or in a category, Annates Scientifiques de L'Université de Clermont, vol. 13 (1976). pp. 1–29.Google Scholar
[32]Soare, R. I., Recursively Enumerable Sets and Degrees, Springer, New York, 1987.CrossRefGoogle Scholar
[33]Whitney, H., On abstract properties of linear dependence, American Journal of Mathematics, vol. 57 (1935), pp. 509–533.CrossRefGoogle Scholar