Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fellows, Michael R.
Szeider, Stefan
and
Wrightson, Graham
2004.
Parameterized and Exact Computation.
Vol. 3162,
Issue. ,
p.
223.
Atserias, Albert
and
Bonet, Marı́a Luisa
2004.
On the automatizability of resolution and related propositional proof systems.
Information and Computation,
Vol. 189,
Issue. 2,
p.
182.
Chinchani, Ramkumar
Ha, Duc
Iyer, Anusha
Ngo, Hung Q.
and
Upadhyaya, Shambhu
2005.
On the Hardness of Approximating the Min-Hack Problem.
Journal of Combinatorial Optimization,
Vol. 9,
Issue. 3,
p.
295.
Fellows, Michael R.
Szeider, Stefan
and
Wrightson, Graham
2006.
On finding short resolution refutations and small unsatisfiable subsets.
Theoretical Computer Science,
Vol. 351,
Issue. 3,
p.
351.
Liberatore, Paolo
2006.
Complexity results on DPLL and resolution.
ACM Transactions on Computational Logic,
Vol. 7,
Issue. 1,
p.
84.
Buresh-Oppenheim, Joshua
and
Mitchell, David
2007.
Theory and Applications of Satisfiability Testing – SAT 2007.
Vol. 4501,
Issue. ,
p.
300.
Peleg, David
2007.
Approximation algorithms for the Label-CoverMAX and Red-Blue Set Cover problems.
Journal of Discrete Algorithms,
Vol. 5,
Issue. 1,
p.
55.
Razborov, Alexander (Sasha)
2007.
Eulogy: Michael (Misha) Alekhnovich 1978-2006.
ACM SIGACT News,
Vol. 38,
Issue. 1,
p.
70.
Alekhnovich, Michael
and
Razborov, Alexander A.
2008.
Resolution Is Not Automatizable Unless W[P] Is Tractable.
SIAM Journal on Computing,
Vol. 38,
Issue. 4,
p.
1347.
Buss, Samuel R.
and
Hoffmann, Jan
2008.
The NP-hardness of finding a directed acyclic graph for regular resolution.
Theoretical Computer Science,
Vol. 396,
Issue. 1-3,
p.
271.
Hoffmann, Jan
2009.
Finding a tree structure in a resolution proof is NP-complete.
Theoretical Computer Science,
Vol. 410,
Issue. 21-23,
p.
2295.
Chinchani, Ramkumar
Ha, Duc
Iyer, Anusha
Ngo, Hung Q.
and
Upadhyaya, Shambhu
2010.
Network Security.
p.
143.
Borodin, A.
Pitassi, T.
and
Razborov, A.
2011.
Special Issue In Memory of Misha Alekhnovich. Foreword.
computational complexity,
Vol. 20,
Issue. 4,
p.
579.
Buss, Samuel R.
2012.
Towards NP–P via proof complexity and search.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 7,
p.
906.
Imanishi, Kensuke
2017.
WALCOM: Algorithms and Computation.
Vol. 10167,
Issue. ,
p.
359.
Atserias, Albert
and
Muller, Moritz
2019.
Automating Resolution is NP-Hard.
p.
498.
Mencía, Carlos
and
Marques-Silva, Joao
2019.
Progress in Artificial Intelligence.
Vol. 11805,
Issue. ,
p.
539.
Atserias, Albert
and
Müller, Moritz
2020.
Automating Resolution is NP-Hard.
Journal of the ACM,
Vol. 67,
Issue. 5,
p.
1.
Hernández-Orozco, Santiago
Hernández-Quiroz, Francisco
Zenil, Hector
and
Sieg, Wilfried
2020.
Shortening of Proof Length is Elusive for Theorem Provers.
Parallel Processing Letters,
Vol. 30,
Issue. 04,
p.
2050013.
Göös, Mika
Koroth, Sajin
Mertz, Ian
and
Pitassi, Toniann
2020.
Automating cutting planes is NP-hard.
p.
68.
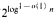 . These results are very robust in that they hold for almost all natural proof systems, including: Frege systems, extended Frege systems, resolution. Horn resolution, the polynomial calculus, the sequent calculus, the cut-free sequent calculus, as well as the polynomial calculus. Our hardness of approximation results usually apply to proof length measured either by number of symbols or by number of inferences, for tree-like or dag-like proofs. We introduce the Monotone Minimum (Circuit) Satisfying Assignment problem and reduce it to the problems of approximation of the length of proofs.
. These results are very robust in that they hold for almost all natural proof systems, including: Frege systems, extended Frege systems, resolution. Horn resolution, the polynomial calculus, the sequent calculus, the cut-free sequent calculus, as well as the polynomial calculus. Our hardness of approximation results usually apply to proof length measured either by number of symbols or by number of inferences, for tree-like or dag-like proofs. We introduce the Monotone Minimum (Circuit) Satisfying Assignment problem and reduce it to the problems of approximation of the length of proofs.



