Article contents
Minimality and completions of PA
Published online by Cambridge University Press: 12 March 2014
Extract
The results in this paper say that natural upper bounds for sets of degrees associated with theories and models of arithmetic cannot be minimal. The basic new result says that for any completion T of PA, there is another completion S such that S<TT and Rep(S) = Rep(T). This immediately implies that deg(T) is not minimal over {deg(X): X ∈ Rep(T)}. As an application of the basic result, we obtain the fact that if 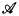 is a non-standard model of TA (true arithmetic), then deg (
is a non-standard model of TA (true arithmetic), then deg (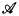 ) cannot be minimal over {deg(X): X is arithmetical}. More generally, if
) cannot be minimal over {deg(X): X is arithmetical}. More generally, if 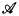 is a non-standard model of an arbitrary completion T of PA, then deg(
is a non-standard model of an arbitrary completion T of PA, then deg(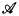 ) cannot be minimal over {deg(
) cannot be minimal over {deg(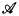 ): X ∈ Rep(T)}. We vary the basic result, making S′ ≡TT′. As an application of the variant, we obtain the fact that if
): X ∈ Rep(T)}. We vary the basic result, making S′ ≡TT′. As an application of the variant, we obtain the fact that if 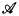 is a non-standard model of PA, then {deg(
is a non-standard model of PA, then {deg(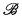 ):
): 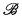 ≅
≅ 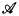 } has no minimal element.
} has no minimal element.
The remainder of the present section gives a brief account of the background needed for the basic new result and the variant. These two results are proved in Section 2. The applications are given in Section 3, along with further background needed for the applications. One important source of ideas used in the present paper is a paper of Scott [9]. In addition, there are ideas taken from Tennenbaum [12], Feferman [3], Marker [6], [7], and Solovay. Chapter 19 of [1] gathers together most of this material. In fact, it contains all that is really essential. In one application, we appeal to Solovay's result on degrees of models of an arbitrary completion of PA, a result which is not completely proved in [1]. However, for the best application, which implies all the others, we use only some ideas from the proof of Solovay's theorem. These are given in lemmas that are proved in Section 3, where they are needed, or taken from [1], While the proof of Solovay's result requires an infinitely nested priority construction, our best application rests on nothing more than finite-injury constructions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 2
- Cited by




