Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-26T19:21:06.570Z Has data issue: false hasContentIssue false
  • English
  • Français

LEBESGUE DENSITY AND 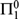$\prod _1^0$ CLASSES

Published online by Cambridge University Press:  09 March 2016

MUSHFEQ KHAN
MUSHFEQ KHAN*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF HAWAII AT MANOA 2565 MCCARTHY MALL (KELLER HALL 401A) HONOLULU, HAWAII 96822, USAE-mail: khan@math.hawaii.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Analyzing the effective content of the Lebesgue density theorem played a crucial role in some recent developments in algorithmic randomness, namely, the solutions of the ML-covering and ML-cupping problems. Two new classes of reals emerged from this inquiry: the positive density points with respect to effectively closed (or 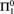$\prod _1^0$) sets of reals, and a proper subclass, the density-one points. Bienvenu, Hölzl, Miller, and Nies have shown that the Martin-Löf random positive density points are exactly the ones that do not compute the halting problem. Treating this theorem as our starting point, we present several new results that shed light on how density, randomness, and computational strength interact.

Keywords

03D3203D7803F6026E40Algorithmic randomnesseffective analysis
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 1 , March 2016 , pp. 80 - 95
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bienvenu, Laurent, Day, Adam R., Greenberg, Noam, Kučera, Antonín, Miller, Joseph S., Nies, André, and Turetsky, Dan, Computing K-trivial sets by incomplete random sets. Bulletin of Symbolic Logic, vol. 20 (2014), no. 1, pp. 80–90.Google Scholar
Bienvenu, Laurent, Greenberg, Noam, Kučera, Antonín, Nies, André, and Turetsky, Dan, Coherent randomness tests and computing the K-trivial sets. Journal of the European Mathematical Society, to appear.Google Scholar
Bienvenu, Laurent, Hölzl, Rupert, Miller, Joseph S., and Nies, André, denjoy, demuth and density. Journal of Mathematical Logic, vol. 14 (2014), no. 1, pp. 1450004, 35.CrossRefGoogle Scholar
Day, Adam R. and Miller, Joseph S., Cupping with random sets. Proceedings of the American Mathematical Society, vol. 142 (2014), no. 8, pp. 2871–2879.Google Scholar
Day, Adam R. and Miller, Joseph S., Density, forcing, and the covering problem. Mathematical Research Letters, vol. 22 (2015), no. 3, pp. 719–727.Google Scholar
Downey, Rodney G. and Hirschfeldt, Denis R., Algorithmic randomness and complexity. Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Figueira, Santiago, Hirschfeldt, Denis, Miller, Joseph S., Ng, Keng Meng, and Nies, André, Counting the changes of random $\Delta _2^0$sets, Programs, Proofs, Processes, vol. 6158, Lecture Notes in Computer Science, pp. 162–171, Springer, Berlin, 2010.Google Scholar
Khan, Mushfeq, Some results on algorithmic randomness and computability-theoretic strength. ProQuest LLC, Ann Arbor, MI, 2014, Ph.D Thesis, The University of Wisconsin - Madison, Madison, WI.Google Scholar
Kurtz, Stuart Alan, Randomness and genericity in the degrees of unsolvability. ProQuest LLC, Ann Arbor, MI, 1981, Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL.Google Scholar
Nies, André, Density and differentiability: dyadic vs full. Logic Blog 2013, http://dl.dropbox.com/u/370127/Blog/Blog2013.pdf.Google Scholar
Nies, André, Computability and randomness, vol. 51, Oxford Logic Guides, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
Nies, André, Stephan, Frank, and Terwijn, Sebastiaan A., Randomness, relativization and Turing degrees, this Journal, vol. 70 (2005), no. 2, pp. 515–535.Google Scholar