Hostname: page-component-84b7d79bbc-fnpn6 Total loading time: 0 Render date: 2024-07-31T22:34:14.238Z Has data issue: false hasContentIssue false
  • English
  • Français

LEARNING THEORY IN THE ARITHMETIC HIERARCHY

Published online by Cambridge University Press:  18 August 2014

ACHILLES A. BEROS
ACHILLES A. BEROS*
Affiliation:
LABORATOIRE INFORMATIQUE DE NANTES ATLANTIQUE, 2, RUE DE LA HOUSSINIÉRE, BP 92208, 44322 NANTES CEDEX 3, FRANCEE-mail: achilles.beros@univ-nantes.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the arithmetic complexity of index sets of uniformly computably enumerable families learnable under different learning criteria. We determine the exact complexity of these sets for the standard notions of finite learning, learning in the limit, behaviorally correct learning and anomalous learning in the limit. In proving the 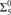${\rm{\Sigma }}_5^0$-completeness result for behaviorally correct learning we prove a result of independent interest; if a uniformly computably enumerable family is not learnable, then for any computable learner there is a 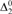${\rm{\Delta }}_2^0$ enumeration witnessing failure.

Keywords

Primary 03D8068Q32inductive inferencelearning theoryarithmetic hierarchy
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 3 , September 2014 , pp. 908 - 927
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Angluin, Dana, Inductive inference of formal languages from positive data. Information and Control, vol. 45 (1980), pp. 117–135.Google Scholar
Bārzdiņš, Janis, Two theorems on the limit synthesis of functions. Theory of Algorithm and Programs, vol. 1 (1974), pp. 82–88.Google Scholar
Bārzdiņš, Janis and Freivalds, Rūsiņš, Prediction of general recursive functions. Doklady Akademii Nauk SSSR, vol. 206 (1972), pp. 521–524.Google Scholar
Blum, Lenore and Blum, Manuel, Toward a mathematical theory of inductive inference. Information and Control, vol. 28 (1975), pp. 125–155.Google Scholar
Gold, Mark, Language identification in the limit, Information and Control, vol. 10 (1967), pp. 447–474.Google Scholar
Osherson, Daniel, Stob, Michael, and Weinstein, Scott, Systems that learn: An introduction to learning theory for cognitive and computer scientists, MIT Press, Cambridge, MA, 1986.Google Scholar
Osherson, Daniel and Weinstein, Scott, Criteria of language learning, Information and Control, vol. 52 (1982), pp. 123–138.Google Scholar
Soare, Robert I., Recursively enumerable sets and degrees: A study of computable functions and computably generated sets, Springer-Verlag, Berlin, Heidelberg, 1987.Google Scholar