Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-10T21:36:49.402Z Has data issue: false hasContentIssue false
  • English
  • Français

INITIAL SEGMENTS OF THE 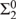${\rm{\Sigma }}_2^0 $ ENUMERATION DEGREES

Published online by Cambridge University Press:  09 March 2016

HRISTO GANCHEV  and
ANDREA SORBI
HRISTO GANCHEV
Affiliation:
FACULTY OF MATHEMATICS AND INFORMATICS SOFIA UNIVERSITY 1164 SOFIA, BULGARIAE-mail: ganchev@fmi.uni-sofia.bg
ANDREA SORBI
Affiliation:
DIPARTIMENTO DI INGEGNERIA DELL’INFORMAZIONE E SCIENZE MATEMATICHE UNIVERSITÀ DEGLI STUDI DI SIENA I-53100 SIENA, ITALYE-mail: andrea.sorbi@unisi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Using properties of 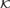${\cal K}$-pairs of sets, we show that every nonzero enumeration degree a bounds a nontrivial initial segment of enumeration degrees whose nonzero elements have all the same jump as a. Some consequences of this fact are derived, that hold in the local structure of the enumeration degrees, including: There is an initial segment of enumeration degrees, whose nonzero elements are all high; there is a nonsplitting high enumeration degree; every noncappable enumeration degree is high; every nonzero low enumeration degree can be capped by degrees of any possible local jump (i.e., any jump that can be realized by enumeration degrees of the local structure); every enumeration degree that bounds a nonzero element of strictly smaller jump, is bounding; every low enumeration degree below a non low enumeration degree a can be capped below a.

Keywords

03D30Enumeration degreesKalimullin pairs
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 1 , March 2016 , pp. 316 - 325
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arslanov, M. M. and Sorbi, A., Relative splittings of ${\rm{\Delta }}_2^0 $in the ${\rm{\Delta }}_2^0 $enumeration degrees, Logic Colloquium ’98 (Buss, S. and Pudlak, P., editors), Springer-Verlag, Heidelberg, 1999.Google Scholar
Badillo, L. and Harris, C. M., Avoiding uniformity in the ${\rm{\Delta }}_2^0 $enumeration degrees. Annals of Pure and Applied Logic, vol. 165 (2014), no. 9, pp. 1355–1379.Google Scholar
Cai, M., Ganchev, H., Lempp, S., Miller, J., and Soskova, M., Defining totality in the enumeration degrees, submitted, 2014.CrossRefGoogle Scholar
Cai, M., Lempp, S., Miller, J., and Soskova, M., On Kalimullin pairs, submitted, 2014.Google Scholar
Cooper, S. B., Partial degrees and the density problem. Part 2: The enumeration degrees of the ${\rm{\Sigma }}_2^0 $sets are dense, this Journal, vol. 49 (1984), pp. 503–513.Google Scholar
Cooper, S. B., Enumeration reducibility, nondeterministic computations and relative computability of partial functions, Recursion Theory Week, Oberwolfach 1989 (Ambos-Spies, K., Müller, G., and Sacks, G. E., editors), Lecture Notes in Mathematics, vol. 1432, pp. 57–110, Springer-Verlag, Heidelberg, 1990.Google Scholar
Cooper, S. B., Computability Theory, Chapman & Hall/CRC Mathematics, Boca Raton, London, New York, Washington, DC, 2003.Google Scholar
Cooper, S. B., Li, A., Sorbi, A., and Yang, Y., Bounding and nonbounding minimal pairs in the enumeration degrees, this Journal, vol. 70 (2005), no. 3, pp. 741–766.Google Scholar
Cooper, S. B. and Sorbi, A., Noncappable enumeration degrees below ${\rm{\Sigma }}_2^0 $, this Journal, vol.61 (1996), pp. 1347–1363.Google Scholar
Cooper, S. B., Sorbi, A., and Yi, X., Cupping and noncupping in the enumeration degrees of ${\rm{\Sigma }}_2^0 $sets. Annals of Pure and Applied Logic, vol. 82 (1997), no. 3, pp. 317–342.Google Scholar
Ellison, P. and Lewis, A. E. M., Joining up to the generalized high degrees. Proceedings of the American Mathematical Society, vol. 138 (2010), no. 8, pp. 2949–2960.CrossRefGoogle Scholar
Friedberg, R. M. and Rogers, H. Jr., Reducibility and completeness for sets of integers. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 5 (1959), pp. 117–125.Google Scholar
Ganchev, H. and Sokova, M., Embedding distributive lattices in the ${\rm{\Sigma }}_2^0 $enumeration degrees. Journal of Logic and Computation, vol. 22 (2012), no. 4, pp. 779–792.Google Scholar
Ganchev, H. and Sokova, M., Cupping and definability in the local structure of the enumeration degrees, this Journal, vol. 77 (2012), no. 1, pp. 133–158.Google Scholar
Ganchev, H. and Sokova, M., Interpreting true arithmetic in the local structure of the enumeration degrees, this Journal, vol. 77 (2012), no. 4, pp. 1184–1194.Google Scholar
Ganchev, H. and Sokova, M., Definability via Kalimullin pairs in the structure of the enumeration degrees. Transactions of the American Mathematical Society, vol. 367 (2015), pp. 4873–4893.Google Scholar
Giorgi, M. B., Sorbi, A., and Yang, Y., Properly ${\rm{\Sigma }}_2^0 $enumeration degrees and the high/low hierarchy, this Journal, vol. 71 (2006), no. 4, pp. 1125–1144.Google Scholar
Harris, C., On the jump classes of noncuppable enumeration degrees, this Journal, vol. 76 (2011), no. 1, pp. 177–197.Google Scholar
Kalimullin, I., Cuppings and cappings in enumeration ${\rm{\Delta }}_2^0 $-degrees. Algebra and Logic, vol. 39 (2000), no. 5, pp. 313–323.Google Scholar
Kalimullin, I., Definability of the jump operator in the enumeration degrees. Journal of Mathematical Logic, vol. 3 (2003), no. 2, pp. 257–267.Google Scholar
Kent, T. F. and Sorbi, A., Bounding nonsplitting enumeration degrees, this Journal, vol. 72 (2007), no. 4, pp. 1405–1417.Google Scholar
Lempp, S. and Sorbi, A., Embedding finite lattices into the ${\rm{\Sigma }}_2^0 $enumeration degrees, this Journal, vol. 67 (2002), no. 1, pp. 69–90.Google Scholar
Lempp, S., Slaman, T. A., and Sorbi, A., On extensions of embeddings into the enumeration degrees of the ${\rm{\Sigma }}_2^0 $-sets. Journal of Mathematical Logic, vol. 5 (2005), no. 2, pp. 247–298.CrossRefGoogle Scholar
McEvoy, K. and Cooper, S. B., On minimal pairs of enumeration degrees, this Journal, vol. 50 (1985), pp. 983–1001.Google Scholar
Posner, D., High Degrees, Ph.D thesis, University of California, Berkeley, 1977.Google Scholar
Sorbi, A., Wu, G., and Yang, Y., High minimal pairs in the enumeration degrees. 6th Annual Conference, TAMC 2009 Changsha, China, May 2009, Lecture Notes in Computer Science, vol. 5532, pp. 335–344, Springer-Verlag, Berlin, Heidelberg, 2009.Google Scholar
Sorbi, A., Wu, G., and Yang, Y., Diamond embeddings in the enumeration degrees. Mathematical Structures in Computer Science, vol. 20 (2010), pp. 799–811.CrossRefGoogle Scholar
Soskova, M. I., A non-splitting theorem in the enumeration degrees. Annals of Pure and Applied Logic, vol. 160 (2009), no. 3, pp. 400–418.Google Scholar