Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-12T03:55:26.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher-Order Illative Combinatory Logic

Published online by Cambridge University Press:  12 March 2014

Łukasz Czajka
Łukasz Czajka*
Affiliation:
Institute of Informatics, University of Warsaw, UL. Banacha 2, 02-097 Warszawa, Poland, E-mail: lukaszcz@mimuw.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

We show a model construction for a system of higher-order illative combinatory logic thus establishing its strong consistency. We also use a variant of this construction to provide a complete embedding of first-order intuitionistic predicate logic with second-order propositional quantifiers into the system 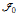of Barendregt, Bunder and Dekkers, which gives a partial answer to a question posed by these authors.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 3 , September 2013 , pp. 837 - 872
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barendregt, Henk, Bunder, Martinw, and Dekkers, Wil, Systems of illative combinatory logic complete for first-order propositional and predicate calculus, this Journal, vol. 58 (1993), no. 3, pp. 769–788.Google Scholar
[2] Bunder, Martin W. and Dekkers, Wil, Pure type systems with more liberal rules, this Journal, vol. 66 (2001), no. 4, pp. 1561–1580.Google Scholar
[3] Bunder, Martin W. and Dekkers, Wil, Equivalences between pure type systems and systems of illative combinatory logic, Notre Dame Journal of Formal Logic, vol. 46 (2005), no. 2, pp. 181–205.Google Scholar
[4] Curry, Haskell B., Feys, Robert, and Craig, William, Combinatory logic, vol. 1, North-Holland, 1958.Google Scholar
[5] Czajka, Łukasz, A semantic approach to illative combinatory logic, Computer Science Logic 2011 (Bezem, Marc, editor), LIPIcs, vol. 12, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2011, pp. 174–188.Google Scholar
[6] Dekkers, Wil, Bunder, Martin W., and Barendregt, Henk, Completeness of the propositions-as-types interpretation of intuitionistic logic into illative combinatory logic, this Journal, vol. 63 (1998), no. 3, pp. 869–890.Google Scholar
[7] Dekkers, Wil, Bunder, Martin W., and Barendregt, Henk, Completeness of two systems of illative combinatory logic for first-order propositional and predicate calculus, Archive for Mathematical Logic, vol. 37 (1998), no. 5-6, pp. 327–341.Google Scholar
[8] Seldin, Jonathan P., The logic of Church and Curry, Logic from Russell to Church (Gabbay, Dov M. and Woods, John, editors), Handbook of the History of Logic, vol. 5, North-Holland, 2009, pp. 819–873.Google Scholar