Shoenfield [6] constructed a hierarchy for any type two object F in which 2E is recursive by generalizing the hyperarithmetical hierarchy, using a jump operation jF defined by

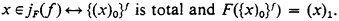
(A similar hierarchy was constructed independently by Hinman [3].) In order to construct a hierarchy for an arbitrary type two F we must first associate with F an operator which, on one hand will always be recursive in F, and on the other hand will generate all the functions recursive in F when iterated over a simultaneously generated set of ordinal notations OF. Clearly the use of 2E in the above definition of jF(f) can be avoided if, instead of diagonalizing F over all functions recursive in f, we only diagonalize F over, say, the functions primitive recursive in f. If furthermore we code in a function which enumerates all functions primitive recursive in f then the resulting operation will certainly generate a primitive recursively expanding hierarchy of functions recursive in F. The problem that remains is whether this hierarchy will exhaust the 1-section of F. But this reduces to an effectiyized version of the following problem: If g is recursive in some level of the hierarchy, is g primitive recursive in some higher level ? An affirmative answer is suggested by the completeness results of Feferman [2], and our main theorem below will be proved by combining his ideas with those of Shoenfield [6]. The result is a hierarchy which applies to all type two objects, and which replaces the notion of recursion in F by the simpler notion of primitive recursion in certain functions generated by F. Unfortunately, in contrast with the Shoenfield hierarchy, the hierarchy developed here cannot always be expected to have the uniqueness property (even w.r.t. ≤T), and for this reason the proof of our main theorem is rather more complicated than the corresponding proof in [6].