Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T21:42:11.923Z Has data issue: false hasContentIssue false
  • English
  • Français

Heirs of box types in polynomially bounded structures

Published online by Cambridge University Press:  12 March 2014

Marcus Tressl
Marcus Tressl*
Affiliation:
University of Manchester, School of Mathematics, Oxford Road, Manchester Ml3 9Pl, UK, E-mail: marcus.tressl@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

A box type is an n-type of an o-minimal structure which is uniquely determined by the projections to the coordinate axes. We characterize heirs of box types of a polynomially bounded o-minimal structure M. From this, we deduce various structure theorems for subsets of Mk, definable in the expansion 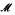of M by all convex subsets of the line. We show that 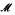after naming constants, is model complete provided M is model complete.

Keywords

model theoryo-minimalityreal closed fieldsheirsweakly o-minimalmodel completenessDedekind cutsvaluation theory
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 4 , December 2009 , pp. 1225 - 1263
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba-Po]Baisalov, Y. and Poizat, B., Paires de structures o-minimales, this Journal, vol. 63 (1998), no. 2, pp. 570–578.Google Scholar
[Do]Dolich, A., Forking and independence in o-minimal theories, this Journal, vol. 69 (2004), no. 1, pp. 215–240.Google Scholar
[Kn]Knebusch, M., Weakly semialgebraic spaces, Lecture Notes in Mathematics, 1367, Springer-Verlag, Berlin, 1989.CrossRefGoogle Scholar
[La]Lascar, D., Stability in model theory, Pitman Monographs and Surveys in Pure and Applied Mathematics, 36, Longman Scientific & Technical, Harlow; John Wiley & Sons, Inc., New York, 1987.Google Scholar
[La-Po]Lascar, D. and Poizat, B., An introduction to forking, this Journal, vol. 44 (1979), no. 3, pp. 330–350.Google Scholar
[MMS]Macpherson, D., Marker, D., and Steinhorn, C., Weakly o-minimal structures and real closed fields, Transactions of the American Mathematical Society, vol. 352 (2000), no. 12, pp. 5435–5483.CrossRefGoogle Scholar
[Ma]Marker, D., Omitting types in o-minimal theories, this Journal, vol. 51 (1986), no. 1, pp. 63–74.Google Scholar
[Ma-St]Marker, D. and Steinhorn, C., Definable types in o-minimal theories, this Journal, vol. 59 (1994), pp. 185–198.Google Scholar
[PS]Pillay, A. and Steinhorn, C., Definable sets in ordered structures I, Bulletin of the American Mathematical Society (N.S.), vol. 11 (1984), no. 1, pp. 159–162.CrossRefGoogle Scholar
[Poi]Poizat, B., Cours de théorie des modèles. Nur al-Mantiq wal-Ma'rifah, Villeurbanne, 1985.Google Scholar
[She 1]Shelah, S., Classification theory and the number of non-isomorphic models, Studies in logic and the foundations of mathematics, North-Holland, Amsterdam, 1978.Google Scholar
[She2]Shelah, S., Dependent first order theories, continued, SH783.Google Scholar
[Sho]Shoenfield, J. R., Mathematical logic, Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills, Ont., 1967.Google Scholar
[Tr1]Tressl, M., Model completeness of o-minimal structures expanded by Dedekind cuts, this Journal, vol. 70 (2005), no. 1, pp. 29–60.Google Scholar
[Tr2]Tressl, M., The elementary theory of dedekind cuts in polynomially bounded structures, Annals of Pure and Applied Logic, vol. 135 (2005), no. 1–3, pp. 113–134.CrossRefGoogle Scholar
[Tr3]Tressl, M., Pseudo completions and completions in stages of o-minimal structures, Archive for Mathematical Logic, vol. 45 (2006), no. 8, pp. 983–1009.CrossRefGoogle Scholar
[Tr4]Tressl, M., Valuation theoretic content of the Marker–Steinhorn Theorem, this Journal, vol. 69 (2004), no. 1, pp. 91–93.Google Scholar
[vdD-Lew]van den Dries, L. and Lewenberg, A. H., t-convexity and tame extensions, this Journal, vol. 60 (1995), no. 1, pp. 74–102.Google Scholar
[vdD-Sp]van den Dries, L. and Speissegger, P., The field of reals with multisummable series and the exponential function, Proceedings of the London Mathematical Society, vol. 81 (2000), no. 3, pp. 513–565.CrossRefGoogle Scholar
[We2]Wencel, R., Topological properties of sets definable in weakly o-minimal structures, preprint, 2005.Google Scholar
[We1]Wencel, R., Weakly o-minimal non-valuational structures, Annals of Pure and Applied Logic, vol. 154 (2008), no. 3, pp. 139–162.CrossRefGoogle Scholar