Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
de Swart, H. C. M.
1985.
Foundations of Logic and Linguistics.
p.
89.
Wasilewska, Anita
1985.
Trees and diagrams of decomposition.
Studia Logica,
Vol. 44,
Issue. 2,
p.
139.
Nie, Jian-Yun
and
Lepage, Francois
1998.
Information Retrieval: Uncertainty and Logics.
p.
17.
Olivetti, Nicola
and
Schwind, Camilla B.
2001.
Theoretical Computer Science.
Vol. 2202,
Issue. ,
p.
384.
Giordano, Laura
Gliozzi, Valentina
Olivetti, Nicola
and
Schwind, Camilla
2003.
Automated Reasoning with Analytic Tableaux and Related Methods.
Vol. 2796,
Issue. ,
p.
81.
Olivetti, Nicola
Pozzato, Gian Luca
and
Schwind, Camilla B.
2007.
A sequent calculus and a theorem prover for standard conditional logics.
ACM Transactions on Computational Logic,
Vol. 8,
Issue. 4,
p.
22.
Olivetti, Nicola
and
Pozzato, Gian Luca
2008.
Theorem proving for conditional logics: CondLean and GOALDUCK.
Journal of Applied Non-Classical Logics,
Vol. 18,
Issue. 4,
p.
427.
Giordano, Laura
Gliozzi, Valentina
Olivetti, Nicola
and
Schwind, Camilla
2009.
Tableau calculus for preference-based conditional logics.
ACM Transactions on Computational Logic,
Vol. 10,
Issue. 3,
p.
1.
Alenda, Régis
Olivetti, Nicola
and
Pozzato, Gian Luca
2012.
Logics in Artificial Intelligence.
Vol. 7519,
Issue. ,
p.
14.
Lellmann, Björn
and
Pattinson, Dirk
2012.
Logics in Artificial Intelligence.
Vol. 7519,
Issue. ,
p.
320.
Olivetti, Nicola
and
Pozzato, Gian Luca
2015.
Automated Reasoning with Analytic Tableaux and Related Methods.
Vol. 9323,
Issue. ,
p.
270.
Alenda, Régis
Olivetti, Nicola
and
Pozzato, Gian Luca
2016.
Nested sequent calculi for normal conditional logics.
Journal of Logic and Computation,
Vol. 26,
Issue. 1,
p.
7.
NEGRI, SARA
and
SBARDOLINI, GIORGIO
2016.
PROOF ANALYSIS FOR LEWIS COUNTERFACTUALS.
The Review of Symbolic Logic,
Vol. 9,
Issue. 1,
p.
44.
Poggiolesi, Francesca
2016.
Natural Deduction Calculi and Sequent Calculi for Counterfactual Logics.
Studia Logica,
Vol. 104,
Issue. 5,
p.
1003.
Girlando, Marianna
Lellmann, Björn
Olivetti, Nicola
and
Pozzato, Gian Luca
2016.
Logics in Artificial Intelligence.
Vol. 10021,
Issue. ,
p.
272.
McCall, McKenna
Loh, Lay Kuan
and
Jia, Limin
2017.
A Sequent Calculus for Counterfactual Reasoning.
p.
91.
Sano, Katsuhiko
and
Ma, Minghui
2019.
Logic and Its Applications.
Vol. 11600,
Issue. ,
p.
132.
Girlando, Marianna
Lellmann, Björn
Olivetti, Nicola
Pesce, Stefano
and
Pozzato, Gian Luca
2022.
Calculi, countermodel generation and theorem prover for strong logics of counterfactual reasoning.
Journal of Logic and Computation,
Vol. 32,
Issue. 2,
p.
233.
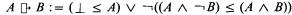 (if A were the case, then B would be the case).
(if A were the case, then B would be the case).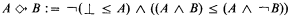 (if A were the case, then B might be the case).
(if A were the case, then B might be the case).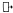 and
and 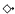 are two counterfactual conditional operators. (A
are two counterfactual conditional operators. (A B) iff ¬(A
B) iff ¬(A ¬B).
¬B).



