Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-23T12:31:21.268Z Has data issue: false hasContentIssue false
  • English
  • Français

Existentially closed torsion-free nilpotent groups of class three1

Published online by Cambridge University Press:  12 March 2014

Berthold J. Maier
Berthold J. Maier*
Affiliation:
Albert-Ludwigs-Universität Freiburg, 78 Freiburg, Federal Republic of Germany, Michigan State University, East Lansing, Michigan 48824
Get access Rights & Permissions [Opens in a new window]

Extract

We denote by 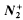and 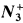the classes of torsion-free nilpotent groups of nilpotency class at most two and three, respectively. In this paper we show that most of the known results about existentially closed (e.c.) groups in 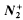remain true in 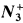: Up to isomorphism, there exist only countably many countable e.c. groups and they are distinguished by the ranks of their centers. An e.c. group is finitely (infinitely) generic if and only if the center has dimension one (≥ω). Apart from trivial exceptions, e.c, algebraically closed, and “closed with respect to systems of equations in one unknown” are equivalent.

Let K be a class of groups. A group G ϵ K is called existentially closed in K if G contains a solution of any finite system Σ of equations and inequations with constants in G and one or more unknowns, provided that Σ has a solution in some 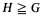in K. If Σ may contain equations (in at most n unknowns) only, G is called algebraically closed (n-unknown closed [1]). We use the abbreviations e.c, a.c and n-u.c. throughout. For more background on these terms the reader is referred to [3] and [4]. We also assume a basic knowledge of generic structures. The main group theoretic notions needed here are explained in §2; [2] and [11] are the general references for this field.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 1 , March 1984 , pp. 220 - 230
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baumslag, B. and Levin, F., Algebraically closed torsion-free nilpotent groups of class 2, Communications in Algebra, vol. 4 (1976), pp. 533–560.CrossRefGoogle Scholar
[2]Baumslag, G., Lecture notes on nilpotent groups, Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, no. 2, American Mathematical Society, Providence, R.I., 1971.Google Scholar
[3]Cherlin, G., Model theoretic algebra—selected topics, Lecture Notes in Mathematics, vol. 521, Springer-Verlag, Berlin, 1976.CrossRefGoogle Scholar
[4]Hirschfeld, J. and Wheeler, W. H., Forcing, arithmetic, division rings, Lecture Notes in Mathematics, vol. 454, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[5]Maier, B. J., Existenziell abgeschlossene Gruppen in nilpotenten Gruppenklassen, Dissertation, Albert-Ludwigs-Universität, Freiburg, 1981.Google Scholar
[6]Maier, B. J., Einbettung von nilpotenten Gruppen zur Erzeugung von Kommutatorrelationen, Communications in Algebra, vol. 10 (1982), pp. 2141–2190.CrossRefGoogle Scholar
[7]Maier, B. J., On existentially closed and generic nilpotent groups, Israel Journal of Mathematics (to appear).Google Scholar
[8]Maier, B. J., Amalgame nilpotenter Gruppen der Klasse zwei, Publicationes Mathematicae (Debrecen) (to appear).Google Scholar
[9]Saracino, D., Existentially complete nilpotent groups, Irael Journal of Mathematics, vol. 25 (1976), pp. 241–248.Google Scholar
[10]Saracino, D., Existentially complete torsion-free nilpotent groups, this Journal, vol. 43 (1978), pp. 126–134.Google Scholar
[11]Schenkman, E., Group theory, Van Nostrand, Princeton, N.J., 1965; reprint, Krieger, New York, 1975s.Google Scholar