Article contents
THE DEFINABILITY STRENGTH OF COMBINATORIAL PRINCIPLES
Published online by Cambridge University Press: 01 December 2016
Abstract
We introduce the definability strength of combinatorial principles. In terms of definability strength, a combinatorial principle is strong if solving a corresponding combinatorial problem could help in simplifying the definition of a definable set. We prove that some consequences of Ramsey’s Theorem for colorings of pairs could help in simplifying the definitions of some 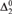 ${\rm{\Delta }}_2^0$ sets, while some others could not. We also investigate some consequences of Ramsey’s Theorem for colorings of longer tuples. These results of definability strength have some interesting consequences in reverse mathematics, including strengthening of known theorems in a more uniform way and also new theorems.
${\rm{\Delta }}_2^0$ sets, while some others could not. We also investigate some consequences of Ramsey’s Theorem for colorings of longer tuples. These results of definability strength have some interesting consequences in reverse mathematics, including strengthening of known theorems in a more uniform way and also new theorems.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2016
References
REFERENCES
- 5
- Cited by




