Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T08:36:42.114Z Has data issue: false hasContentIssue false
  • English
  • Français

A construction of type: type in Martin-Löf's partial type theory with one universe

Published online by Cambridge University Press:  12 March 2014

Erik Palmgren
Erik Palmgren*
Affiliation:
Department of Mathematics, Uppsala University, 752 38 Uppsala, Sweden
Get access Rights & Permissions [Opens in a new window]

Extract

In this note we construct Martin-Löf's inconsistent type theory, Type: Type (Martin-Löf [1971]), inside partial type theory with one universe. Thus adding a fixed point operator to type theory with one predicative universe gives impredicativity.

We may describe the theory Type:Type as follows. It contains the rules for the product construction (II) of Martin-Löf [1984] except the η-rule and it contains the usual rules for definitional equality (=). Moreover it contains the following strongly impredicative universe

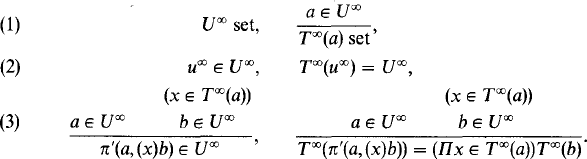
This theory is inconsistent (i.e. every set is inhabited), and this is seen by proving a variant of the Burali—Forti paradox—Girard's paradox—cf. Troelstra and van Dalen [1988]. Coquand [199?] has shown that by adding the well-order type and the strong dependent sum to the universe, the fixed point operator becomes definable. It is an open problem whether it is definable without the well-order type. The present result could be seen as a converse, namely by adding the fixed point operator to type theory with one universe, Type:Type becomes definable and, as is already known, so does the well-order type.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 3 , September 1991 , pp. 1012 - 1015
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Amadio, R., Bruce, K. B., and Longo, G. [1986], The finitary projection model for second order lambda calculus and solutions to higher order domain equations, Logic in computer science (Meyer, A. R., editor), IEEE Computer Society Press, Washington, D.C., pp. 122–130.Google Scholar
Coquand, T. [199?], The paradox of trees in type theory, BIT (to appear).Google Scholar
Coquand, T., Gunter, C., and Winskel, G. [1989], Domain theoretic models of polymorphism, Information and Computation, vol. 81, pp. 123–167.CrossRefGoogle Scholar
Martin-Löf, P. [1971], A theory of types (unpublished manuscript).Google Scholar
Martin-Löf, P. [1984], Intuitionistic type theory, Bibliopolis, Naples.Google Scholar
Martin-Löf, P. [1986], Unifying Scott's theory of domains for denotational semantics and intuitionistic type theory (abstract), Atti del congresso logica e filosofia delta scienza, oggi. San Gimignano 7–11 dicembre 1983. Vol. I: Logica, CLUEB, Bologna.Google Scholar
Martin-Löf, P. [1989], Mathematics of infinity, COLOG-88: proceedings of the international conference on computer logic held in Tallinn, 1988 (Martin-Löf, P. and Mints, G., editors), Lecture Notes in Computer Science, vol. 417, Springer-Verlag, Berlin, 1990, pp. 146–197.CrossRefGoogle Scholar
Palmgren, E. [1989], A domain interpretation of Martin-Löf's partial type theory with universes, Report No. 1989:11, Department of Mathematics, Uppsala University, Uppsala.Google Scholar
Palmgren, E. and Stoltenberg-Hansen, V. [1990], Domain interpretations of Martin-Löf's partial type theory, Annals of Pure and Applied Logic, vol. 48, pp. 135–196.CrossRefGoogle Scholar
Troelstra, A. S. and van Dalen, D. [1988], Constructivism in mathematics. Vol. II, North-Holland, Amsterdam.Google Scholar