Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-21T05:39:35.141Z Has data issue: false hasContentIssue false
  • English
  • Français

THE COMPLEXITY OF INDEX SETS OF CLASSES OF COMPUTABLY ENUMERABLE EQUIVALENCE RELATIONS

Published online by Cambridge University Press:  01 December 2016

URI ANDREWS  and
ANDREA SORBI
URI ANDREWS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF WISCONSIN MADISON, WI 53706-1388, USAE-mail: andrews@math.wisc.eduURL: http://www.math.wisc.edu/∼andrews/
ANDREA SORBI
Affiliation:
DIPARTIMENTO DI INGEGNERIA INFORMATICA E SCIENZE MATEMATICHE UNIVERSITÀ DEGLI STUDI DI SIENA I-53100 SIENA, ITALYE-mail: andrea.sorbi@unisi.itURL: http://www3.diism.unisi.it/∼sorbi/
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 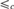$ \le _c $ be computable the reducibility on computably enumerable equivalence relations (or ceers). We show that for every ceer R with infinitely many equivalence classes, the index sets 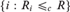$\left\{ {i:R_i \le _c R} \right\}$ (with R nonuniversal), 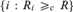$\left\{ {i:R_i \ge _c R} \right\}$, and 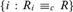$\left\{ {i:R_i \equiv _c R} \right\}$ are 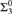${\rm{\Sigma }}_3^0$ complete, whereas in case R has only finitely many equivalence classes, we have that 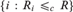$\left\{ {i:R_i \le _c R} \right\}$ is 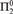${\rm{\Pi }}_2^0$ complete, and 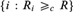$\left\{ {i:R \ge _c R} \right\}$ (with R having at least two distinct equivalence classes) is 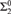${\rm{\Sigma }}_2^0$ complete. Next, solving an open problem from [1], we prove that the index set of the effectively inseparable ceers is 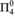${\rm{\Pi }}_4^0$ complete. Finally, we prove that the 1-reducibility preordering on c.e. sets is a 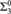${\rm{\Sigma }}_3^0$ complete preordering relation, a fact that is used to show that the preordering relation 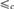$ \le _c $ on ceers is a 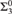${\rm{\Sigma }}_3^0$ complete preordering relation.

Keywords

03D25computably enumerable equivalence relationcomputable reducibility on equivalence relations
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 4 , December 2016 , pp. 1375 - 1395
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andrews, U., Lempp, S., Miller, J. S., Ng, K. M., San Mauro, L., and Sorbi, A., Universal computably enumerable equivalence relations, this Journal, vol. 79 (2014), no. 1, pp. 60–88.Google Scholar
Bernardi, C. and Sorbi, A., Classifying positive equivalence relations, this Journal, vol. 48 (1983), no. 3, pp. 529–538.Google Scholar
Case, J., Periodicity in generations of automata . Mathematical Systems Theory, vol. 8 (1974), pp. 15–32.Google Scholar
Coskey, S., Hamkins, J. D., and Miller, R., The hierarchy of equivalence relations on the natural numbers. Computability, vol. 1 (2012), pp. 15–38.Google Scholar
Ershov, Yu. L., Positive equivalences . Algebra and Logic, vol. 10 (1973), no. 6, pp. 378–394.Google Scholar
Ershov, Yu. L., Theory of Numberings, Nauka, Moscow, 1977.Google Scholar
Fokina, E. B., Friedman, S. D., and Nies, A., Equivalence relations that are ${\rm{\Sigma }}_3^0$ complete for computable reducibility - (Extended Abstract), WoLLIC, Springer, Berlin, Heidelberg, New York, 2012, pp. 26–33.Google Scholar
Fokina, E. B., Friedman, S. D., Harizanov, V., Knight, J. F., Mccoy, C., and Montalbán, A., Isomorphism relations on computable structures, this Journal, vol. 77 (2012), no. 1, pp. 122–132.Google Scholar
Fokina, E., Khoussainov, B., Semukhin, P., and Turetsky, D., Linear orders realized by c.e. equivalence relations, this Journal, to appear.Google Scholar
Gao, S. and Gerdes, P., Computably enumerable equivalence realations . Studia Logica, vol. 67 (2001), pp. 27–59.Google Scholar
Gravruskin, A., Jain, S., Khoussainov, A., and Stephan, F., Graphs realized by r.e. equivalence relations . Annals of Pure and Applied Logic, vol. 165 (2014), no. 7, pp. 1263–1290.CrossRefGoogle Scholar
Gravuskin, A., Khoussainov, A., and Stephan, F., Reducibilities among equivalence relations induced by recursively enumerable structures . Theoretical Computer Science, vol. 612 (2016), no. 25, pp. 137–152.Google Scholar
Ianovski, E., Miller, R., Nies, A., and Ng, K. M., Complexity of equivalence relations and preorders from computability theory, this Journal, vol. 79 (2014), no. 3, pp. 859–881.Google Scholar
Lachlan, A. H., A note on positive equivalence relations . Zeitschrift fur mathematische Logik und Grundlagen der Mathematik, vol. 33 (1987), pp. 43–46.CrossRefGoogle Scholar
Montagna, F., Relative precomplete numerations and arithmetic . Journal of Philosophical Logic, vol. 11 (1982), pp. 419–430.CrossRefGoogle Scholar
Montagna, F. and Sorbi, A., Universal recursion theoretic properties of r.e. preordered structures, this Journal, vol. 50 (1985), no. 2, pp. 397–406.Google Scholar
Odifreddi, P., Classical Recursion Theory, vol. II. Studies in Logic and the Foundations of Mathematics, vol. 143, North-Holland, Amsterdam, 1999.Google Scholar
Pour-El, M. B. and Kripke, S., Deduction preserving isomorphisms between theories . Fundamenta Mathematicae, vol. 61 (1967), pp. 141–163.Google Scholar
San Mauro, L., Forma e complessità. Uno studio dei gradi delle relazioni di equivalenza ricorsivamente enumerabili , Master’s thesis, University of Siena, 2011. (in Italian).Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Heidelberg, 1987.Google Scholar