Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-23T09:31:08.363Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLEXITY OF EQUIVALENCE RELATIONS AND PREORDERS FROM COMPUTABILITY THEORY

Published online by Cambridge University Press:  18 August 2014

EGOR IANOVSKI ,
RUSSELL MILLER ,
KENG MENG NG  and
ANDRÉ NIES
EGOR IANOVSKI
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF OXFORD WOLFSON BUILDING, PARKS ROAD OXFORD OX1 3QD, UK.Email: egor.ianovski@cs.ox.ac.uk
RUSSELL MILLER
Affiliation:
DEPARTMENT OF MATHEMATICS, QUEENS COLLEGE 65-30 KISSENA BLVD., FLUSHING NY 11367 USA; & PH.D. PROGRAMS IN MATHEMATICS & COMPUTER SCIENCE CUNY GRADUATE CENTER, 365 FIFTH AVENUE, NEW YORK, NY 10016, USAE-mail: Russell.Miller@qc.cuny.edu
KENG MENG NG
Affiliation:
DIVISION OF MATHEMATICAL SCIENCES SCHOOL OF PHYSICAL & MATHEMATICAL SCIENCES NANYANG TECHNOLOGICAL UNIVERSITY 21 NANYANG LINK, SINGAPOREE-mail: kmng@ntu.edu.sg
ANDRÉ NIES
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE, UNIVERSITY OF AUCKLAND PRIVATE BAG 92019, AUCKLAND, NEW ZEALANDE-mail: andre@cs.auckland.ac.nz
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the relative complexity of equivalence relations and preorders from computability theory and complexity theory. Given binary relations R, S, a componentwise reducibility is defined by

R ≤ S ⇔ ∃f ∀x, y [x R y ↔ f (x) S f (y)].

Here, f is taken from a suitable class of effective functions. For us the relations will be on natural numbers, and f must be computable. We show that there is a 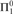${\rm{\Pi }}_1^0$-complete equivalence relation, but no 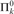${\rm{\Pi }}_k^0$-complete for k ≥ 2. We show that 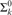${\rm{\Sigma }}_k^0$ preorders arising naturally in the above-mentioned areas are 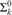${\rm{\Sigma }}_k^0$-complete. This includes polynomial time m-reducibility on exponential time sets, which is 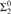${\rm{\Sigma }}_2^0$, almost inclusion on r.e. sets, which is 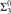${\rm{\Sigma }}_3^0$, and Turing reducibility on r.e. sets, which is 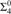${\rm{\Sigma }}_4^0$.

Keywords

Primary 03D78Secondary 03D32computable reducibilitycomputability theoryequivalence relationsm-reducibilityrecursion theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 3 , September 2014 , pp. 859 - 881
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ambos-Spies, Klaus, Antimitotic recursively enumerable sets, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 31 (1985), pp. 461–467.Google Scholar
Ambos-Spies, Klaus, Inhomogeneities in the polynomial time degrees, Information Processing Letters, vol. 22 (1986), pp. 113–117.Google Scholar
Andrews, Uri, Lempp, Steffen, Miller, Joseph S., Ng, Keng Meng, SanMauro, Luca, and Sorbi, Andrea, Universal computably enumerable equivalence relations, submitted.Google Scholar
Balcázar, J. L., Díaz, J., and Gabarró, J., Structural Complexity I, vol. 11, EATCS Monographs on Theoretical Computer Science, Springer-Verlag, Heidelberg, 1988.Google Scholar
Bernardi, Claudio and Sorbi, Andrea, Classifying positive equivalence relations, this Journal, vol. 48 (1983), no. 3, pp. 529–538.Google Scholar
Buss, Sam, Chen, Yijia, Flum, Jörg, Friedman, Sy-David, and Müller, Moritz, Strong isomorphism reductions in complexity theory, this Journal, vol. 76 (2011), pp. 1381–1402.Google Scholar
Calvert, Wesley, The isomorphism problem for classes of computable fields, Archive for Mathematical Logic, vol. 43 (2004), no. 3, pp. 327–336.Google Scholar
Calvert, Wesley, Harizanov, Valentina S., Knight, Julia F., and Miller, Sara, Index sets for computable structures, Algebra and Logic, vol. 353 (2001), pp. 491–518.Google Scholar
Camerlo, Riccardo and Gao, Su, The completeness of the isomorphism relation for countable Boolean algebras, Transactions of the American Mathematical Society, vol. 67 (2001), no. 1, pp. 27–59.Google Scholar
Cholak, Peter, Dzhafarov, Damir, Schweber, Noah, and Shore, Richard, Computably enumerable partial orders, Computability, vol. 1 (2012), no. 2, pp. 99–107.Google Scholar
Coskey, Samuel, Hamkins, Joel D., and Miller, Russell, The hierarchy of equivalence relations on the natural numbers under computable reducibility, Computability, vol. 1 (2012), no. 1, pp. 15–38.Google Scholar
Ershov, Yu. L., Theory of numberings, Nauka, 1977.Google Scholar
Fokina, Ekaterina B., Friedman, Sy-David, Harizanov, Valentina, Knight, Julia F., McCoy, Charles, and Montalbán, Antonio, Isomorphism relations on computable structures, this Journal, vol. 77 (2012), no. 1, pp. 122–132.Google Scholar
Fokina, Ekaterina B. and Friedman, Sy-David, On ${\rm{\Sigma }}_1^1 $equivalence relations over the natural numbers, Mathematical Logic Quarterly, vol. 58 (2012), no. 1–2, pp. 113–124.Google Scholar
Fokina, Ekaterina B., Friedman, Sy-David, and Nies, André, Equivalence relations that are ${\rm{\Sigma }}_3^0 $complete for computable reducibility (extended abstract), In Logic, Language, Information and Computation (Ong, Luke and de Queiroz, Ruy, editors), Proceedings of WoLLIC 2012, Lecture Notes in Computer Science, vol. 7456, Springer, pp. 26–33.Google Scholar
Fortnow, Lance and Grochow, Joshua A., Complexity classes of equivalence problems revisited, Information and Computation, vol. 209 (2011), no. 4, pp. 748–763.Google Scholar
Gao, Su, Invariant descriptive set theory, Pure and Applied Mathematics (Boca Raton), vol. 293, CRC Press, Boca Raton, FL, 2009.Google Scholar
Gao, Su and Gerdes, Peter, Computably enumerable equivalence relations, Studia Logica, vol. 67 (2001), no. 1, pp. 27–59.Google Scholar
Ianovski, Egor, Computable component-wise reducibility, MSc thesis, University of Auckland, 2012, available at http://arxiv.org/abs/1301.7112.Google Scholar
Kuske, Dietrich, Liu, Jiamou, and Lohrey, Markus, The isomorphism problem on classes of automatic structures, 25th Annual IEEE Symposium on Logic in Computer Science LICS, 2010, IEEE Computer Society, Los Alamitos, CA, pp. 160–169.Google Scholar
Lyndon, Roger C. and Schupp, Paul E., Combinatorial group theory, Springer-Verlag, 1977.Google Scholar
Maass, Wolfgang and Stob, Mike, The intervals of the lattice of recursively enumerable sets determined by major subsets, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 189–212.Google Scholar
Melnikov, Alexander G. and Nies, André, The classification problem for compact computable metric spaces, In CiE, 2013, pp. 320–328.Google Scholar
Montagna, Franco and Sorbi, Andrea, Universal recursion-theoretic properties of r.e. preordered structures, this Journal, vol. 50 (1985), no. 2, pp. 397–406.Google Scholar
Nies, André, A uniformity of degree structures, In Complexity, logic, and recursion theory, Lecture Notes in Pure and Applied Mathematics, vol. 187, Dekker, New York, 1997, pp. 261–276.Google Scholar
Nies, André, Coding methods in computability theory and complexity theory, Habilitationsschrift, Universität Heidelberg, 1998, available at http://arxiv.org/abs/1308.6399.Google Scholar
Odifreddi, Piergiorgio, Strong reducibilities, Bulletin of the American Mathematical Society, vol. 4 (1981), no. 1, pp. 37–86.Google Scholar
Pour-El, Marian Boykan and Kripke, Saul, Deduction-preserving “recursive isomorphisms” between theories, Fundamenta Mathematicae, vol. 61 (1967), pp. 141–163.Google Scholar
Smullyan, Raymond, Theory of Formal Systems, Annals of Mathematical Studies, vol. 47, Princeton University Press, Princeton, NJ, 1961.Google Scholar
Soare, Robert I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Heidelberg, 1987.Google Scholar