Article contents
The completeness theorem for infinitary logic
Published online by Cambridge University Press: 12 March 2014
Extract
It will be proven that a set of sentences of infinitary logic is satisfiable iff it is proof theoretically consistent. Since this theorem is known to be false, it must be quickly added that an extended notion of model is being used; truth values may be taken from an arbitrary complete Boolean algebra. We shall give a Henkin style proof of this result which generalizes easily to Boolean valued sets of sentences.
For each infinite candinal number κ the language Lκ is built up from a set of relation symbols together with a constant symbol cα and a variable υα for each α in κ. It contains atomic formulas and is closed under the following rules:
(1) If Γ is a set of formulas of power < κ ∧ Γ is a set of formulas.
(2) If φ is a formula, ¬ φ is also.
(3) If φ is a formula and A Is a subset of κ of power < κ then Aφ is a formula.
∧Γ is meant to be the conjunction of all the formulas in Γ, while Aφ is the universal quantification of all the variables υα for α in A. We let C denote the set of constant symbols in Lκ, the parameter κ must be discovered from the context.
A model is identified with its truth function. Thus a model is a function 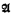 mapping the sentences of Lκ into a complete Boolean algebra which satisfies the following conditions:
mapping the sentences of Lκ into a complete Boolean algebra which satisfies the following conditions:
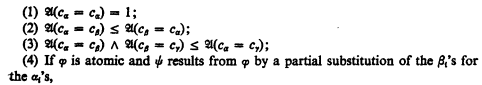
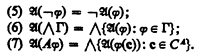
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
BIBLIOGRAPHY
- 4
- Cited by




