Article contents
Cofinitary groups, almost disjoint and dominating families
Published online by Cambridge University Press: 12 March 2014
Abstract
In this paper we show that it is consistent with ZFC that the cardinality of every maximal cofinitary group of Sym(ω) is strictly greater than the cardinal numbers 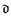 and
and 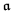 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 5
- Cited by




