Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-27T15:27:32.815Z Has data issue: false hasContentIssue false
  • English
  • Français

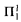– CA0 and order types of countable ordered groups

Published online by Cambridge University Press:  12 March 2014

Reed Solomon
Reed Solomon*
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, Madison. WL 57305., USA, E-mail: rsolomon@math.wisc.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Reverse mathematics uses subsystems of second order arithmetic to determine which set existence axioms are required to prove particular theorems. Surprisingly, almost every theorem studied is either provable in RCA0 or equivalent over RCA0 to one of four other subsystems: WKL0, ACA0, ATR0 or 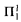– CA0. Of these subsystems, 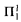– CA0 has the fewest known equivalences. This article presents a new equivalence of 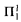– C0 which comes from ordered group theory.

One of the fundamental problems about ordered groups is to classify all possible orders for various classes of orderable groups. In general, this problem is extremely difficult to solve. Mal'tsev [1949] solved a related problem by showing that the order type of a countable ordered group is ℤαℚε where ℤ is the order type of the integers, ℚ is the order type of the rationals, α is a countable ordinal, and ε is either 0 or 1. The goal of this article is to prove that this theorem is equivalent over RCA0 to 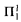– CA0.

In Section 2, we give the basic definitions and notation for RCA0, ACA0 and 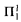CA0 as well as for ordered groups. For more information on reverse mathematics, see Friedman, Simpson, and Smith [1983] or Simpson [1999] and for ordered groups, see Kokorin and Kopytov [1974] or Fuchs [1963]. Our notation will follow these sources. In Section 3, we show that 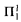– CA0 suffices to prove Mal'tsev's Theorem and the reversal is done over RCA0 in Section 4.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 1 , March 2001 , pp. 192 - 206
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Friedman, Harvey M. and Hirst, Jeffrey L. [1990], Weak comparability of well orderings and reverse mathematics, Annals of Pure and Applied Logic, vol. 47, pp. 11–29.CrossRefGoogle Scholar
Friedman, Harvey M., Simpson, Stephen G., and Smith, Rick L. [1983], Countable algebra and set existence axioms, Annals of Pure and Applied Logic, vol. 25, pp. 141–181.CrossRefGoogle Scholar
Fuchs, L. [1963], Partially ordered algebraic systems, Pergamon Press.Google Scholar
Hirst, Jeffry L. [1999], Ordinal inequalities, transfinite induction, and reverse mathematics, this Journal, vol. 64, no. 2, pp. 769–774.Google Scholar
Jockusch, Carl G. Jr. and Soare, Robert I. [1991], Degrees of orderings not isomorphic to recursive linear orderings, Annals of Pure and Applied Logic, vol. 52, pp. 39–64.CrossRefGoogle Scholar
Kokorin, A.I. and Kopytov, V.M. [1974], Fully ordered groups, Halsted Press.Google Scholar
Kunen, Kenneth [1980], Set theory an introduction to independence proofs, North-Holland.Google Scholar
Mal'tsev, A.I. [1949], On ordered groups, Izvestiya Akademii Nauk SSSR Seriya Matematicheskaya, vol. 13, pp. 473–482, (Russian).Google Scholar
Simpson, Stephen G. [1999], Subsystems of second order arithmetic, Springer-Verlag.CrossRefGoogle Scholar
Soare, Robert I. [1987], Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag.CrossRefGoogle Scholar
Solomon, David Reed [1998], Reverse mathematics and ordered groups, Ph.D. Thesis, Cornell University.Google Scholar
Solomon, David Reed [1999], Ordered groups: a case study in reverse mathematics, The Bulletin of Symbolic Logic, vol. 5, no. 2, pp. 45–58.CrossRefGoogle Scholar