Article contents
BOREL FUNCTORS AND INFINITARY INTERPRETATIONS
Published online by Cambridge University Press: 05 October 2018
Abstract
We introduce the notion of infinitary interpretation of structures. In general, an interpretation between structures induces a continuous homomorphism between their automorphism groups, and furthermore, it induces a functor between the categories of copies of each structure. We show that for the case of infinitary interpretation the reversals are also true: every Baire-measurable homomorphism between the automorphism groups of two countable structures is induced by an infinitary interpretation, and every Baire-measurable functor between the set of copies of two countable structures is induced by an infinitary interpretation. Furthermore, we show that the complexities are maintained in the sense that if the functor is 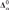 ${\bf{\Delta }}_\alpha ^0$, then the interpretation that induces it is
${\bf{\Delta }}_\alpha ^0$, then the interpretation that induces it is 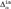 ${\rm{\Delta }}_\alpha ^{in}$ up to
${\rm{\Delta }}_\alpha ^{in}$ up to 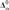 ${\bf{\Delta }}_\alpha ^0$ equivalence.
${\bf{\Delta }}_\alpha ^0$ equivalence.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
Footnotes
Current address: DEPARTMENT OF PURE MATHEMATICS UNIVERSITY OF WATERLOO CANADA E-mail: maharris@math.uwaterloo.caURL: http://www.math.uwaterloo.ca/∼maharris/
References
REFERENCES
- 6
- Cited by




