Article contents
Baire numbers, uncountable Cohen sets and perfect-set forcing
Published online by Cambridge University Press: 12 March 2014
Extract
The Baire number of the real line (see 1.1(c)) has uncountable cofinality [Mi]. This number is equal to the Baire number of the space 2ω and also to the Baire number (1.1(d)) of every countable partial order. Our research is motivated by the following open question (1.13) (see also [BPS] and [Mi]): can the cofinality of nκ, the Baire number of the space (2κ)κ (1.1(b)), be less than or equal to κ? This question is nontrivial when κ is regular and 2κ = κ (1.3). A. Miller proved that the answer is “no” if κ is strongly inaccessible (see [Mi] and 1.11). Assuming CH, 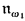 is equal to the Baire number of the Stone space of ℘(ω)/Fin.
is equal to the Baire number of the Stone space of ℘(ω)/Fin.
In §1 we discuss 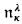 , the Baire number of the space (2λ)κ. If κ is regular, then
, the Baire number of the space (2λ)κ. If κ is regular, then 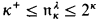 , and using 1.3 and 1.5, we may rule out the easy cases and restrict ourselves to cases where κ is regular with 2<κ = κ, and κ ≤ λ 2κ. If λ > κ, then it is consistent to have cof(
, and using 1.3 and 1.5, we may rule out the easy cases and restrict ourselves to cases where κ is regular with 2<κ = κ, and κ ≤ λ 2κ. If λ > κ, then it is consistent to have cof(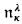 )=κ ([Mi] and 1.7). We do not know whether
)=κ ([Mi] and 1.7). We do not know whether 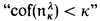 is consistent (1.9). Next, the cardinal number eκ is defined (1.10). It is easy to see that nκ ≤ eκ and that cof(eκ) > κ. If κ is strongly inaccessible (s.i.), then nκ = eκ ([Mil], [Bar], [MF] and 1.11). For κ accessible, the question of whether nκ = eκ is open.
is consistent (1.9). Next, the cardinal number eκ is defined (1.10). It is easy to see that nκ ≤ eκ and that cof(eκ) > κ. If κ is strongly inaccessible (s.i.), then nκ = eκ ([Mil], [Bar], [MF] and 1.11). For κ accessible, the question of whether nκ = eκ is open.
Another open question (Fremlin) is stated as follows: assume W ⊇ V and f ∈ ωω ∩ W is such that, for every g ∈ ω ω ∩ V, ∣(f = g)∣ = ℵ0, does this imply that W contains sets which are ω-Cohen (1.1(a)) over V? If κ is accessible regular with 2<κ = κ, then the answer to the analog of Fremlin's question for κ is “no”. In fact, any κ-closed forcing that adds new subsets of κ, also adds a new function f ∈ κκ such that, for every g ∈ κκ ∩V, (f = g) is stationary (4.1(a)). On the other hand, perfect-set forcing on κ (see [Ka] and §5) adds a new subset of κ but produces a minimal extension (5.4(b)), and hence adds no sets which are κ-Cohen over V.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 12
- Cited by




